99클럽 코테 스터디 29일차 TIL (Missing Number) - LeetCode

벌써 8월 중순을 넘어 말이다… 시간은 왜이리 빠를까요??

8월 4주차 월요일, 다시 열심히 출발해볼까요?

오늘 문제는 99클럽 코테 스터디 29일차 문제로 이진 탐색 유형의 문제입니다.

---

1. 오늘의 학습 키워드

• 리스트
• 이진 탐색

---

2. 문제: 268. Missing Number

• 단계: Easy
• 주제: Array, Hash Table, Math, Binary Search, Bit Manipulation, Sorting
• 출처: https://leetcode.com/problems/missing-number/

문제 설명

Given an array nums containing n distinct numbers in the range [0, n], return the only number in the range that is missing from the array.

Example 1:

Input: nums = [3,0,1]
Output: 2
Explanation: n = 3 since there are 3 numbers, so all numbers are in the range [0,3]. 2 is the missing number in the range since it does not appear in nums.

Example 2:

Input: nums = [0,1]
Output: 2
Explanation: n = 2 since there are 2 numbers, so all numbers are in the range [0,2]. 2 is the missing number in the range since it does not appear in nums.

Example 3:

Input: nums = [9,6,4,2,3,5,7,0,1]
Output: 8
Explanation: n = 9 since there are 9 numbers, so all numbers are in the range [0,9]. 8 is the missing number in the range since it does not appear in nums.

Constraints:

• n == nums.length
• 1 <= n <= 104
• 0 <= nums[i] <= n
• All the numbers of nums are unique.

Follow up: Could you implement a solution using only O(1) extra space complexity and O(n) runtime complexity?

---

3. 나의 풀이

접근 방법

오늘 문제를 보기전 유형이 이진탐색이라고 해서, 이진 탐색으로 풀어야지~ 하고 접근했습니다. 하지만 문제를 보자마자, 이진 탐색을 활용해서 푸는것보다 훨씬 간단한 방법이 떠올랐습니다.

문제를 살펴보면 주어진 nums 리스트가 있는데 이것은 원래 0부터 n까지의 정수가 담긴 ([0, n] ) 리스트입니다. 이 상황에서 nums 리스트에서 [0, n] 리스트 대비 없는 값을 찾는 문제입니다.

설명이 길었던거 같은데 한 문장으로 요약하자면,

배열 nums가 [0, n] 범위 내의 n개의 서로 다른 숫자를 포함하고 있을 때, 배열에 없는 유일한 숫자를 반환하는 문제입니다!

첫번째 예시를 살펴볼까요?

nums = [3, 0, 1] 이 주어졌습니다. 이것은 원래 0부터 3까지의 값이 주어져야하는 리스트인데 nums를 보시면 2가 빠진것을 알 수 있습니다.

자, 감이 오시나요? 이 문제를 푸는 방법은 매우 많을것 같지만 제가 생각한 방법은

리스트의 합에서 nums 리스트의 합을 빼면 nums 리스트에 없는 숫자를 얻을수 있게 됩니다.

1부터 n 까지의 합 공식을 아래와 같습니다:

$n*(n+1)\over 2$

이 수식을 기반으로 코드 구현은 아래와 같습니다:

class Solution(object):
    def missingNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """      
        return len(nums)*(len(nums)+1) // 2 - sum(nums)

1. nums 리스트는 0부터 들어있기 때문에, len()함수를 사용하면 수식과 동일한 의미로 사용될 수 있습니다.
2. len()함수의 시간복잡도는 O(1)입니다. 만약 max()함수를 사용했다면 O(n)이기 때문에 len()함수를 사용하는게 효율적입니다.
3. sum()함수의 시간복잡도는 O(n)이므로 이 코드의 시간복잡도는 O(n)입니다.

코드의 결과는 아래와 같습니다.

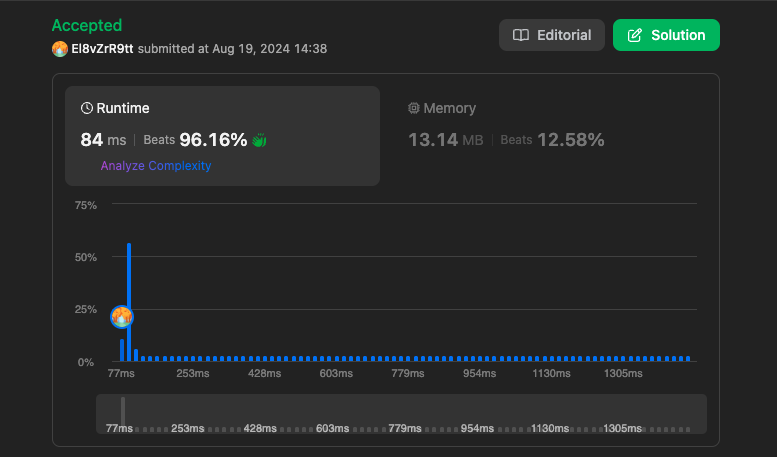
https://leetcode.com/problems/missing-number/submissions/1361014811

확실히 속도적으로 좋은 결과를 보여주고 있습니다.

만약 max()함수를 사용했을 때의 결과는 아래와 같이 나왔습니다:

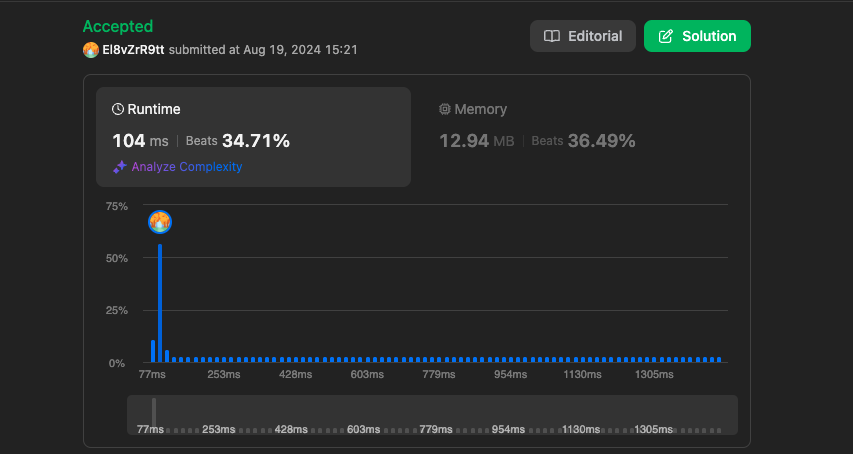
https://leetcode.com/problems/missing-number/submissions/1361050444

len()함수를 사용한 것보다 속도가 약간 느려진 것을 확인할 수 있습니다.

---

4. 다른 풀이

이전에 제가 이 문제의 유형이 이진 탐색이였다고 말씀 드렸습니다. 이제 이진 탐색으로 풀어볼까요?

이진 탐색이란?

이진 탐색은 정렬된 리스트에서 검색 범위를 절반으로 줄여 나가면서 검색 값을 찾는 알고리즘입니다.

이진 탐색에서 중요한 것은 정렬된 리스트에서 진행한다는 점입니다. 리스트의 크기가 클수록 완전 탐색보다 확실히 효율적인 것은 맞습니다. 하지만 리스트가 정렬되어야 하기 때문에 이미, o(nlogn)의 시간복잡도가 생깁니다.

따라서, 이 문제를 풀기에는 이전의 방법이 훨씬 효율적이였던 것입니다.

이진 탐색을 활용한 코드는 아래와 같습니다:

class Solution(object):
    ###################### 이진 탐색 ######################
    def missingNumber(self,nums):

        nums.sort()  # O(nlogn)

        left, right = 0, len(nums)-1

        while left <= right:
            med = (left+right) // 2

            if nums[med] > med:
                right = med - 1
            else:
                left = med + 1
        
        return left
    ###################### 이진 탐색 ######################

코드 설명:

1. 정렬:
   • nums.sort()를 사용하여 배열을 오름차순으로 정렬합니다. 시간 복잡도는 O(nlogn)입니다.
2. 이진 탐색:
   • left와 right 변수를 초기화하여 배열의 처음과 끝을 가리키게 합니다.
   • 이진 탐색 루프에서 배열의 중간 인덱스 med를 계산합니다.
   • 만약 nums[med]가 med보다 크다면, 이는 중간 인덱스 이전에 누락된 숫자가 있다는 뜻이므로 right를 med - 1로 이동합니다.
   • 그렇지 않으면, 누락된 숫자는 중간 인덱스 이후에 있으므로 left를 med + 1로 이동합니다.
   • 루프가 끝나면 left는 배열에서 누락된 숫자가 위치해야 하는 인덱스를 가리킵니다.

결과 (이진 탐색 반복문 풀이)

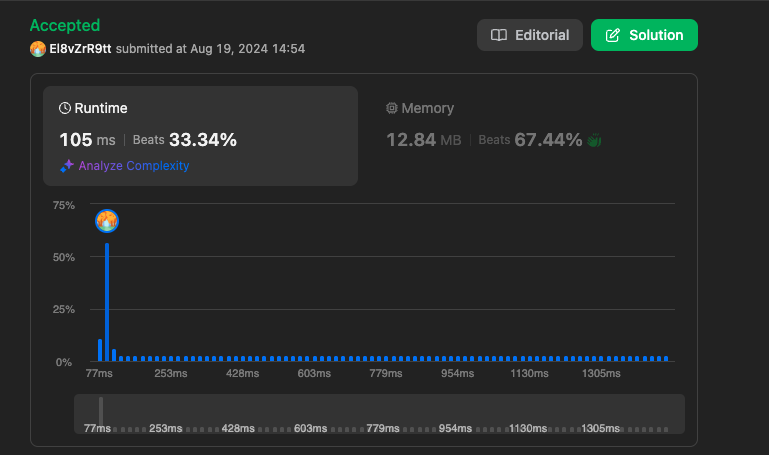
https://leetcode.com/problems/missing-number/submissions/1361027876

위 코드는 반복문을 활용한 이진 탐색 구현 방법입니다. 하지만 이진 탐색은 재귀 함수를 통해서도 구현이 가능합니다. 재귀 함수를 활용해서 구현해보겠습니다.

class Solution(object):
    def missingNumber(self, nums):
        nums.sort()  # O(nlogn)
        return self.binarySearch(nums, 0, len(nums) - 1)

    def binarySearch(self, nums, left, right):
        if left > right:
            return left

        med = (left + right) // 2

        if nums[med] > med:
            return self.binarySearch(nums, left, med - 1)
        else:
            return self.binarySearch(nums, med + 1, right)

코드 설명:

1. 정렬: 먼저 nums.sort()로 배열을 정렬합니다. 이 과정의 시간 복잡도는 O(nlog⁡n)O(n \log n)O(nlogn)입니다.
2. 이진 탐색 재귀 함수:
   • binarySearch 함수는 배열 nums와 인덱스 left, right를 인자로 받습니다.
   • 기저 사례: left가 right보다 큰 경우, 탐색이 완료된 상태로, 누락된 숫자가 위치할 인덱스인 left를 반환합니다.
   • 중간 인덱스 계산: med는 (left + right) // 2로 계산됩니다.
   • 재귀 호출:
     • 만약 nums[med]가 med보다 크다면, 누락된 숫자는 왼쪽에 있으므로 right를 med - 1로 설정하고 재귀 호출합니다.
     • 그렇지 않다면, 누락된 숫자는 오른쪽에 있으므로 left를 med + 1로 설정하고 재귀 호출합니다.

결과 (이진 탐색 재귀 함수 풀이)

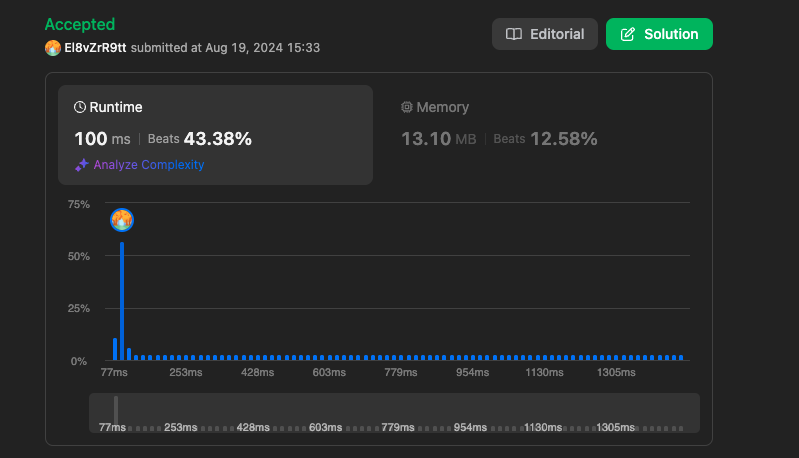
https://leetcode.com/problems/missing-number/submissions/1361060974

---

이렇게 이진 탐색으로도 해결이 가능한 문제였습니다. 그런데!! 이 문제의 주제가 기억나시나요?

• 주제: Array, Hash Table, Math, Binary Search, Bit Manipulation, Sorting

지금까지 푼 방법은 Array, Math, Binary Search, Sorting들을 활용한 방법이라 볼 수 있죠. 하지만 아직 Hash Table과 Bit Manipulation 방법을 활용해서도 풀 수 있다는 것을 확인할 수 있습니다.

Hash Table 풀이

Hash Table은 생각하진 못했지만 구현은 해보았습니다.

class Solution(object):
    
    def missingNumber(self,nums):
        
        nums_dict = {}
        
        for i in nums:
            if i not in nums_dict:
                nums_dict[i] = 1
        print(nums_dict)
        
        for i in range(len(nums)+1):
            print(i)

이 코드는 해시맵(딕셔너리)을 사용하여 배열에서 누락된 숫자를 찾는 방법을 구현한 것입니다. 이 코드가 어떻게 작동하는지와 그 시간 복잡도에 대해 설명하겠습니다.

코드 설명:

1. 딕셔너리 생성:

   • 먼저 빈 딕셔너리 nums_dict를 생성합니다.
   • 그 다음, nums 배열의 모든 요소를 순회하면서, 해당 숫자가 딕셔너리에 없으면 추가합니다. 이때 값으로 1을 넣습니다.
   • 이 과정이 끝나면, nums_dict에는 배열의 모든 숫자가 키로 존재하게 됩니다.

   nums_dict = {}
   for i in nums:
       if i not in nums_dict:
           nums_dict[i] = 1
   

   예를 들어, nums = [3, 0, 1]인 경우, nums_dict는 {3: 1, 0: 1, 1: 1}가 됩니다.

2. 누락된 숫자 찾기:

   • 이제 0부터 n까지의 숫자를 순회하면서, 그 숫자가 nums_dict에 없는지 확인합니다.
   • 만약 없는 숫자를 찾으면, 그것이 누락된 숫자이므로 반환합니다.
   • 이 코드에서 i가 nums_dict의 key에 있는지를 확인합니다.

   for i in range(len(nums) + 1):
       if i not in nums_dict:
           return i
   

   예를 들어, nums = [3, 0, 1]인 경우, range(len(nums) + 1)은 range(4)로, 0, 1, 2, 3을 탐색합니다. 여기서 2는 딕셔너리에 없으므로 반환됩니다.

시간 복잡도:

1. 딕셔너리 생성:
   • 배열 nums를 한 번 순회하며 딕셔너리를 채우는 작업의 시간 복잡도는 O(n)입니다.
2. 누락된 숫자 찾기:
   • range(len(nums) + 1)을 순회하며 각 숫자가 딕셔너리에 있는지 확인하는 작업의 시간 복잡도도 (O(n)입니다.
   • 딕셔너리에서 특정 키가 존재하는지 확인하는 작업은 O(1)이므로, 전체적으로 이 부분도 O(n)입니다.

총 시간 복잡도:

이 코드의 총 시간 복잡도는 O(n)입니다. 이 방식은 해시맵을 사용하기 때문에 매우 효율적이며, 정렬을 필요로 하지 않기 때문에 빠르게 누락된 숫자를 찾을 수 있습니다.

공간 복잡도:

딕셔너리를 추가적으로 사용하고 있으므로 공간 복잡도는 O(n)입니다.

결과 (Hash Table 풀이)

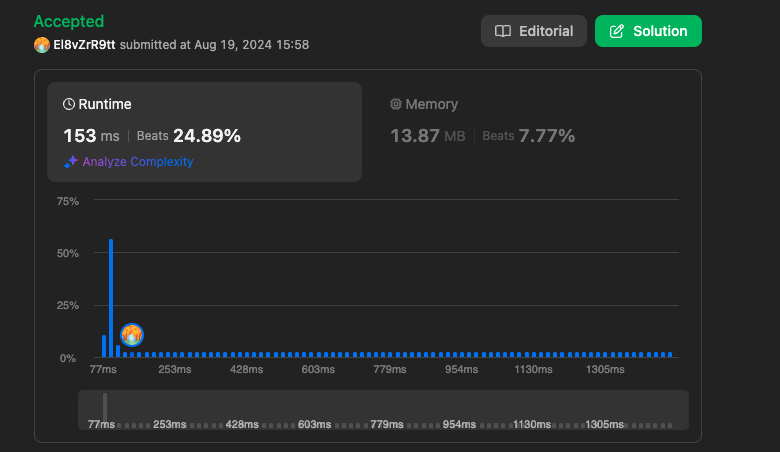
https://leetcode.com/problems/missing-number/submissions/1361082612

Bit manipulation 풀이

아쉽게도 비트 연산자는 잘 몰라서 서칭을 해보았습니다.

주어진 배열 nums는 0부터 n까지의 n개의 서로 다른 숫자 중 일부를 포함하고 있습니다. 배열에서 빠진 유일한 숫자를 찾아야 합니다.

XOR 연산의 특징

XOR은 "Exclusive OR"의 약자로, 이진수 연산에서 두 비트가 다를 때 1을 반환하고, 같을 때 0을 반환하는 논리 연산입니다.

• XOR 진리표:

  A	B	A XOR B
  0	0	0
  0	1	1
  1	0	1
  1	1	0

• XOR의 주요 성질:
  1. a ^ a = 0: 같은 값을 XOR하면 0이 됩니다.
  2. a ^ 0 = a: 어떤 수를 0과 XOR하면 그 수 자체가 됩니다.
  3. 교환 법칙: a ^ b = b ^ a (순서에 관계없이 결과가 같습니다).
  4. 결합 법칙: (a ^ b) ^ c = a ^ (b ^ c) (묶는 순서에 관계없이 결과가 같습니다).

이러한 특성 때문에, 숫자들이 쌍을 이루어 있는 경우 XOR을 사용하면 쌍을 이루지 않는 숫자만 남게 됩니다.

이것을 예시로 보면 다음과 같습니다.

a = [0, 1, 2, 3]
nums = [0, 1, 3]

쌍을 맞춰서 보면,

• 0 ^ 0 = 0
• 1 ^ 1 = 0
• 3 ^ 3 = 0

최종적으로 0과 2를 비교하면 0 ^ 2 는 2가 나옵니다. 이렇게 쌍을 맞춰서 비교하면 남는 값이 나오기 때문에 XOR를 활용해서 접근할 수 있는겁니다.

해결 전략

문제를 해결하기 위해 두 가지 XOR 연산을 사용할 것입니다:

1. 0부터 n까지의 모든 숫자를 XOR 연산으로 합칩니다.
2. 주어진 배열 nums의 모든 숫자를 XOR 연산으로 합칩니다.
3. 이 두 결과를 다시 XOR 연산하면, 배열에서 빠진 숫자가 남게 됩니다.

이 방법이 작동하는 이유는, 배열에 있는 숫자들은 두 번째 XOR에서 모두 상쇄되지만, 배열에 없는 숫자는 남기 때문입니다.

코드 구현

class Solution(object):
    def missingNumber(self, nums):
        xor_all = 0
        xor_nums = 0

        # 1. 0부터 n까지의 숫자를 모두 XOR합니다.
        for i in range(len(nums) + 1):
            xor_all ^= i

        # 2. nums 배열에 있는 모든 숫자를 XOR합니다.
        for num in nums:
            xor_nums ^= num

        # 3. 두 XOR의 결과를 다시 XOR하여 누락된 숫자를 찾습니다.
        return xor_all ^ xor_nums

코드 설명

1. 전체 범위 XOR:

   • xor_all 변수는 0부터 n까지의 모든 숫자를 XOR한 값을 저장합니다.
   • 이 과정의 시간 복잡도는 O(n)입니다.

   xor_all = 0
   for i in range(len(nums) + 1):
       xor_all ^= i
   

2. 배열의 모든 요소 XOR:

   • xor_nums 변수는 배열 nums에 있는 모든 숫자를 XOR한 값을 저장합니다.
   • 이 과정의 시간 복잡도도 O(n)입니다.

   xor_nums = 0
   for num in nums:
       xor_nums ^= num
   

3. 결과 XOR:

   • 마지막으로 xor_all과 xor_nums를 XOR하여 배열에서 빠진 숫자를 찾습니다. 이 숫자가 반환됩니다.

   return xor_all ^ xor_nums
   

예시

nums = [3, 0, 1]이라고 가정해 봅시다:

1. xor_all = 0 ^ 1 ^ 2 ^ 3 = 0
2. xor_nums = 3 ^ 0 ^ 1 = 2
3. xor_all ^ xor_nums = 0 ^ 2 = 2

여기서 2는 배열에 없는 숫자입니다.

시간 복잡도

• 시간 복잡도: 이 방법은 O(n) 시간 복잡도를 가집니다. 각 단계에서 배열을 한 번씩 순회하기 때문입니다.
• 공간 복잡도: 추가 메모리를 거의 사용하지 않으므로, 공간 복잡도는 O(1) 입니다.

결과 (XOR 풀이)

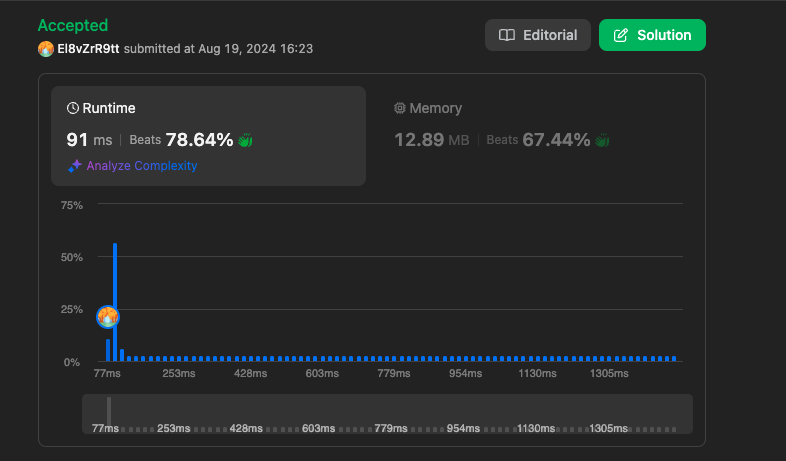
https://leetcode.com/problems/missing-number/submissions/1361102195

자연수의 합을 활용한 풀이 다음으로 속도가 빠른것을 확인할 수 있습니다.

다섯가지의 코드에 대한 테스트 케이스 결과 및 걸린 시간 측정을 진행한 코드는 아래 링크를 통해 확인할 수 있습니다.

https://github.com/jw9603/Python/blob/main/99%E1%84%8F%E1%85%B3%E1%86%AF%E1%84%85%E1%85%A5%E1%86%B8/Beginner/29%E1%84%8B%E1%85%B5%E1%86%AF%E1%84%8E%E1%85%A1/1.py

---

5. 결론

이번 문제는 간단한 문제였지만 풀이 방법이 정말 다양하고 배울것이 많은 문제였습니다.

이진탐색, 해쉬, 구현 (math), 비트 연산자 (XOR)등의 개념을 익히는 데 정말 도움이 되는 문제라고 생각합니다.

궁금하신 내용이 있으시면 댓글은 언제든지 환영입니다.

읽어주셔서 감사합니다!