99클럽 코테 스터디 30일차 TIL (Arranging Coins) - LeetCode

시간이 너무 부족한 요즘..! 포기하지말고 꾸준하게 나아가자!

오늘은 8월 20일 99클럽 코테 스터디 30일차 TIL입니다.

이 문제는 어제 문제와 동일하게 이진 탐색 유형의 문제입니다. 하지만 어제와 동일하게 이진 탐색이 아닌 수학적 방법으로도 풀 수 있는 문제입니다.

한 번 알아볼까요?

---

1. 오늘의 학습 키워드

• 리스트
• math
• binary search

---

2. 문제: 441. Arranging Coins

• 단계: Easy
• 주제: Math, Binary Search
• 출처: https://leetcode.com/problems/arranging-coins/

문제 설명

You have n coins and you want to build a staircase with these coins. The staircase consists of k rows where the ith row has exactly i coins. The last row of the staircase may be incomplete.

Given the integer n, return the number of complete rows of the staircase you will build.

Example 1:

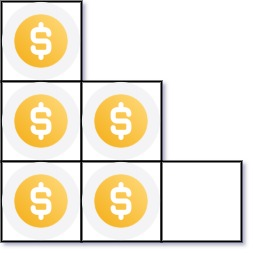
Input: n = 5
Output: 2
Explanation: Because the 3rd row is incomplete, we return 2.

Example 2:

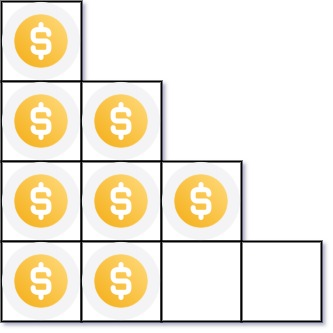
Input: n = 8
Output: 3
Explanation: Because the 4th row is incomplete, we return 3.

Constraints:

• 1 <= n <= 231 - 1

---

3. 나의 풀이

저는 참 멍청합니다.. 이 문제를 보고 생각보다 시간 소요가 많았습니다. 문제를 살펴보시면 n 개의 코인이 주어지고 이것을 오른쪽으로 한 칸씩 늘어나는 계단형태로 돈을 쌓습니다. 여기서 계단의 층별로 가득 채워질 수있는 계단의 층 수를 구하는 것이 이 문제입니다.

문제를 보고 저는 n 을 1부터 쭈욱 예시를 살펴보면서 규칙을 찾고 있었는데요.

규칙은 찾았습니다. 하지만 이 규칙은 이진 탐색과 직접적인 연관은 없었고, 오히려 DP알고리즘을 사용해야 하나? 싶었습니다. 그래서 다시 처음 문제로 돌아가서 시작을 했는데요.

문제를 잘 보시면 저와 같은 이상한 짓? 은 하지 않을수 있습니다.

1층에 동전 1개, 2층에 동전 2개, 3층에는 동전 3개가 들어갈 수있습니다.

즉, x층 계단에는 x개의 동전이 들어갑니다.

문제에서는 총 코인의 수 n 개가 주어집니다. 그러면 1층부터 x층까지의 코인수를 다 더해서 n 개의 코인이 되는것입니다.

문제는 완전히 채워지는 계단의 수를 원하는데, 이것은 1층부터 x층까지의 코인수의 합이 n 과 같아지도록 하는 x를 구하면 된다는 것입니다.

어제 TIL을 보시면 1부터 n까지의 정수합을 다음과 같이 구했습니다:

$n*(n+1)\over 2$

$n$을 $x$로 치환하고 n개의 코인이 1부터 x층까지의 합에 대한 수식을 구하면 아래와 같습니다:

${x*(x+1)\over {2}} = n$

이 수식은 2차 방정식의 해를 구하는 과정을 통해 구할수 있습니다.

따라서, 코드를 보시면 아래와 같습니다:

import math
class Solution(object):
    def arrangeCoins(self, n):
        """
        :type n: int
        :rtype: int
        """

        return int((-1 + math.sqrt(1 + 8 * n)) // 2)

설명:

• 이 접근법은 계단 형태의 총 동전 수가 k(k + 1) / 2임을 이용하여 문제를 해결합니다.
• 이 식을 풀어 k에 대한 식을 유도하면 k = (-1 + sqrt(1 + 8 * n)) / 2가 됩니다.
• 여기서 sqrt는 제곱근을 계산하고, 최종적으로 k를 정수로 변환하여 반환합니다.

시간 복잡도:

• 이 방법의 시간 복잡도는 O(1)입니다. 이는 입력 크기에 상관없이 일정한 시간 안에 결과를 계산할 수 있음을 의미합니다. 왜냐하면, 상수 시간 안에 수행되는 수학적 연산만 필요하기 때문입니다.

정말 간단하죠?

이렇게 실전에서 기발한? 아이디어가 떠오르면 좋겠네요!

결과는 아래와 같이 나왔습니다.

Result (math)

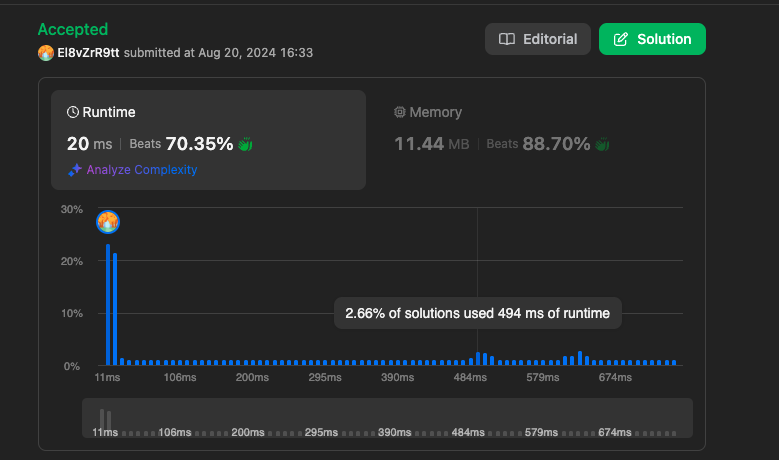
https://leetcode.com/problems/arranging-coins/submissions/1362169109

---

4. 다른 풀이

LeetCode의 장점은 해당 문제의 topics을 알 수 있는점입니다. topics에는 다양한 것들이 있을수 있는데요. 이 문제의 topic은 Binary Search였습니다.

아직, Binary search에 대해 익숙하지 않은것 같습니다. 반복만이 살 길이겠죠?

이진 탐색 유형인지는 몰랐지만 이진 탐색 유형이란 것을 알고는 그래도 구현은 성공했습니다.

이진 탐색은 반복, 재귀적 방법으로 풀 수 있습니다. 이 두 가지 방법 모두 구현을 진행했습니다. 한 번 살펴볼까요?

1. 이분 탐색 (반복적 접근, Iterative Binary Search)

class Solution(object):
    def arrangeCoins(self, n):
        low, high = 1, n

        while low <= high:
            mid = (low + high) // 2
            current = mid * (mid + 1) // 2

            if current == n:
                return mid
            elif current < n:
                low = mid + 1
            else:
                high = mid - 1

        return high

설명:

• 이 방법은 이분 탐색을 사용하여 k(k + 1) / 2 <= n을 만족하는 최대의 k를 찾습니다.
• low와 high는 탐색 범위를 나타내며, 중간 값 mid에 대해 mid * (mid + 1) // 2가 n보다 크거나 작은지에 따라 탐색 범위를 좁혀갑니다.
• 마지막으로 high를 반환하면, 이 값이 최대 완전한 계단을 형성할 수 있는 k입니다.

시간 복잡도:

• 이 방법의 시간 복잡도는 O(log n)입니다. 이는 이분 탐색이 매 단계마다 탐색 범위를 절반으로 줄이기 때문에 로그 시간 안에 결과를 찾을 수 있음을 의미합니다.

Result (Iterative Binary Search)

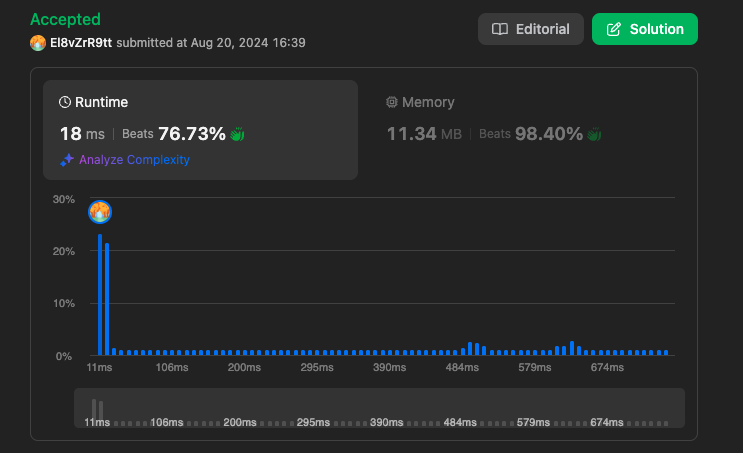
https://leetcode.com/problems/arranging-coins/submissions/1362173528

2. 이분 탐색 (재귀적 접근, Recursive Binary Search)

class Solution(object):
    def arrangeCoins(self, n):
        return self.binarySearch(n, 1, n)

    def binarySearch(self, n, low, high):
        if low > high:
            return high

        mid = (low + high) // 2
        current = mid * (mid + 1) // 2

        if current == n:
            return mid
        elif current < n:
            return self.binarySearch(n, mid + 1, high)
        else:
            return self.binarySearch(n, low, mid - 1)

설명:

• 이 방법은 위의 이분 탐색 방법과 동일한 논리를 사용하지만, 반복 대신 재귀적으로 구현됩니다.
• 재귀 호출을 통해 탐색 범위를 좁혀가며, 최종적으로 탐색 범위가 역전되었을 때 high를 반환합니다.

시간 복잡도:

• 이 방법의 시간 복잡도도 O(log n)입니다. 반복적 접근 방식과 마찬가지로, 탐색 범위를 절반씩 줄이기 때문에 로그 시간에 문제를 해결할 수 있습니다.
• 다만, 재귀적으로 호출 스택이 쌓이므로 공간 복잡도는 O(log n)이 됩니다.

Result (Recursive Binary Search)

https://leetcode.com/problems/arranging-coins/submissions/1362177392

실행 결과를 보시면 수학적 방법의 시간복잡도가 O(1)로 가장 빠르지만 실제 결과는 오히려 제일 느린것을 확인할 수 있습니다.

저는 이것이 궁금해서 로컬에서도 한 번 테스트 케이스에 대한 속도 측정도 진행해보았습니다. 여기서도 마찬가지로, 수학적 방법이 가장 느린것을 확인했습니다. 이것에 대한 이유를 보자면 제 나름대로의 추측입니다.

1. math 모듈의 호출로 인한 오버헤드
   1. 수학적 계산과 관련된 오버헤드가 포함될 수 있으며, 특히 작은 입력값에 대해서는 오히려 반복문이 더 빠를 수 있습니다.
2. math 모듈의 함수 계산 비용
   1. 수학적 접근법에서는 math.sqrt()와 같은 외부 라이브러리 함수를 호출하게 됩니다. 이 함수 호출은 추가적인 오버헤드를 초래할 수 있습니다.

큰 차이는 안나지만, 이렇게 사소한 분석이 나중에 큰 힘이 될 것이라고 믿습니다!

---

5. 결론

이번 문제도 이진 탐색 유형의 문제였지만 간단한 코드가 존재하는 문제였습니다.

역시 코딩테스트는 많은 양의 문제와 반복만이 살 길이라는 것을 다시 한 번 깨달았습니다.

또한, 문제를 풀기전 선택한 알고리즘 (방법)에 대한 설계와 이유 및 근거, 시간 복잡도를 어느정도 알고 접근하는 것이 훨씬 효율적이라는 것도 깨달은 하루 입니다.

궁금하신 내용은 댓글!! 언제나 환영입니다.

읽어주셔서 감사합니다:)

TMI)

졸업하는데 논문 쓸 수도… ㅠ