[LeetCode] 104. Maximum Depth of Binary Tree

말하는 감자·2024년 11월 13일
BFSDFSbinary treeleetcodepythontreetree traversal
1

LeetCode

목록 보기
8/32
post-thumbnail

오늘 문제는 어제 문제에 이어서 이진 트리에 관한 문제입니다.

1. 오늘의 학습 키워드

  • Tree
  • Binary Tree
  • DFS
  • BFS

2. 문제: 104. Maximum Depth of Binary Tree

Description

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

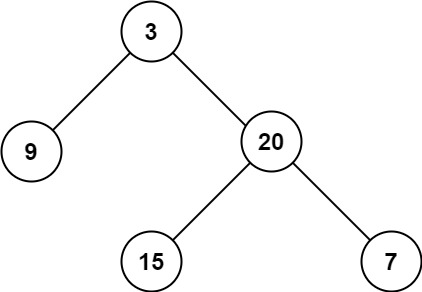
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [0, $10^4$].
  • -100 <= Node.val <= 100

3. 문제 풀이

Binary Tree 하나가 주어집니다. 주어진 binary tree의 최대 깊이를 구하는 문제입니다. 최대 깊이는 흔히 하는 트리에서의 Level이라 보시면 됩니다.

그럼 차근차근 문제를 짚어보겠습니다.

Step1. 문제 이해하기

  • Input:
    • node개수는 0부터 10410^4입니다. 이는 노드 가 아예 없을수도 있다는 것을 의미합니다. 또한, 트리 문제는 순회 위주의 문제로 많이 구성되기 때문에 O(n)O(n)의 시간복잡도로 코드를 구현한다면 될 것으로 보입니다.
    • 노드 값이 -100부터 100사이에 있기 때문에 int, char값을 가질수도 있으며, 중복이 허용됩니다. 물론 이 내용은 코드 구현하는 데 크게 영향을 미치지는 않을것입니다.
  • Output:
    • 최대 깊이를 반환합니다.

해당 문제의 Input을 통해서 알 수 있는 것은 확실히 트리 순회를 활용하는 문제임을 알 수 있었습니다. 그렇다면 어떤 순회를 사용해야 할까요?

Step2. 문제 분석

Step1에서 문제의 input을 통해 어떤 알고리즘으로 구색을 갖춰야 할 지 찾았습니다.

해당 문제는 이진 트리이고 O(n2)O(n^2)보다 작은 시간복잡도로 코드를 구현해야 합니다.

이는 트리 순회를 활용할 수 있음을 의미합니다.

그럼 이제 문제의 의미를 살펴보겠습니다.

문제는 루트 노드부터 마지막 자식 노드까지의 깊이를 구하는 문제입니다. 확실히 문제가 의미하는 것이 트리 내 노드를 순회하면서 깊이를 측정하면 될 것으로 보입니다.

제가 이전에 최대 깊이는 최대 레벨을 의미한다고 했습니다. 그렇기 때문에 처음 떠오른 순회 알고리즘은 level-order traversal (BFS)였습니다. 레벨마다 트리를 순회하면서 레벨(깊이)를 측정하면 될 것으로 보입니다.

첫번째 예시를 보겠습니다.

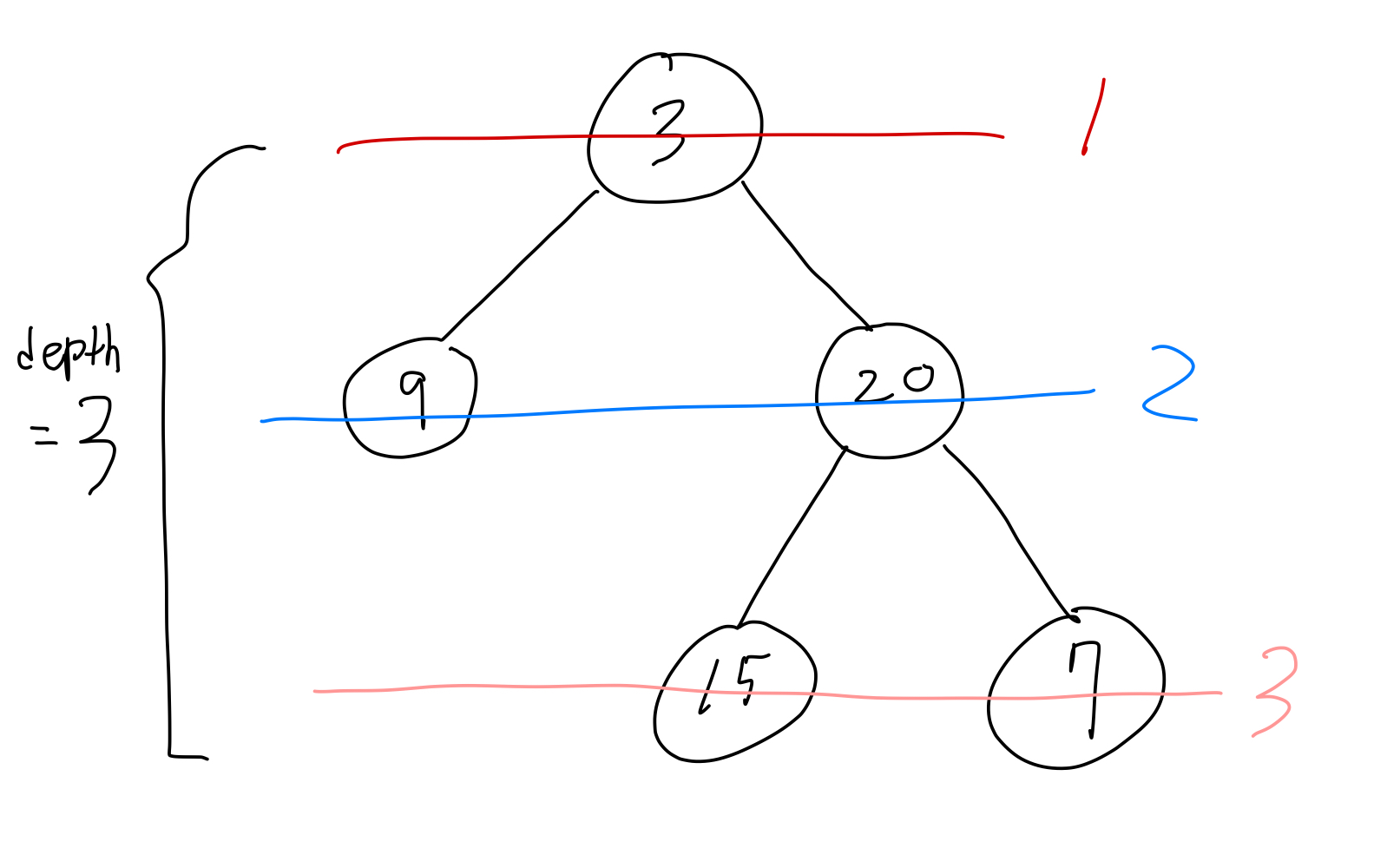
level order 순회를 하면 3 → 9 → 20 → 15 → 7이 됩니다. 레벨이 바뀔때마다 depth를 1개씩 증가하면 구할 수 있습니다.

Step3. 코드 설계

트리 순회에서 level order traversal (BFS)는 정말 중요한 알고리즘입니다. 정말 입력하면 바로 나올 정도로 외워야 합니다. BFS를 생각하면 떠오르는 자료구조가 있죠? 바로 큐 자료구조입니다. 좌, 우 방향만 정해지면 시작 노드의 자식 노드 순으로 방문을 하기 때문에 큐 자료 구조를 활용하면 쉽게 설계가 가능합니다.

순회는 말 그대로 순회입니다. 하지만 방문은 노드들을 순회하면서 어떤 행동을 하는것이죠. 저희는 최대 깊이를 구하는 것이 문제입니다. 그렇다는 것은 노드를 방문하면서 깊이 체크를 하는것입니다. 순회를 하면서 방문한 노드를 출력하는 것이 아닌 깊이 체크를 진행하면 됩니다.

그럼 코드를 구현해보겠습니다.

Step4. 코드 구현

from collections import deque

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
        
class Solution(object):
    
    # 1. Level Order Traversal
    def maxDepth(self,root):
        """
        :type root: Optional[TreeNode]
        :rtype: int
        """
        if root is None:
            return 0

        max_depth = 0
        q = deque()
        q.append((root,1))

        while q:
            cur_node,cur_depth = q.popleft()
            max_depth = max(max_depth, cur_depth)
            if cur_node.left:
                q.append((cur_node.left,cur_depth+1))
            if cur_node.right:
                q.append((cur_node.right,cur_depth+1))
        return max_depth

코드 설명:

  1. maxDepth 함수는 트리의 깊이를 계산하기 위해 BFS(Level Order Traversal)를 사용합니다.
  2. 큐(deque)를 사용하여 루트 노드부터 시작해 레벨마다 모든 노드를 순회합니다.
  3. 각 노드가 큐에서 빠질 때마다 현재 레벨(깊이)을 max_depth와 비교해 최대 깊이를 갱신합니다.
  4. 큐에 자식 노드가 있을 경우, 각 자식 노드의 깊이를 1 증가시켜 추가하여 다음 레벨로 이동합니다.
  5. 최종적으로 max_depth에는 트리의 최대 깊이가 저장되며 이를 반환합니다.

시간 복잡도: O(n), 트리의 모든 노드를 한 번씩 방문하므로 n은 노드 수를 의미합니다.

결과:

https://leetcode.com/problems/maximum-depth-of-binary-tree/submissions/1451221766

4. 다른 풀이

처음에 접근은 level order traversal, BFS를 활용하여 문제를 풀었습니다. 하지만 이 문제는 DFS로도 풀 수 있습니다. 왜냐하면 트리 순회를 활용하는 문제이기 때문에, level order이나, 깊이 기반의 순회이나 큰 차이가 없기 때문이죠.

저는 다시 한 번 봤을 때, 떠오른 방법은 Post order traversal이였습니다. 기존의 level order traversal은 위에서 부터 시작했습니다. 그럼 밑에서 부터 시작하면 어떨까요?

예시 1을 보겠습니다.

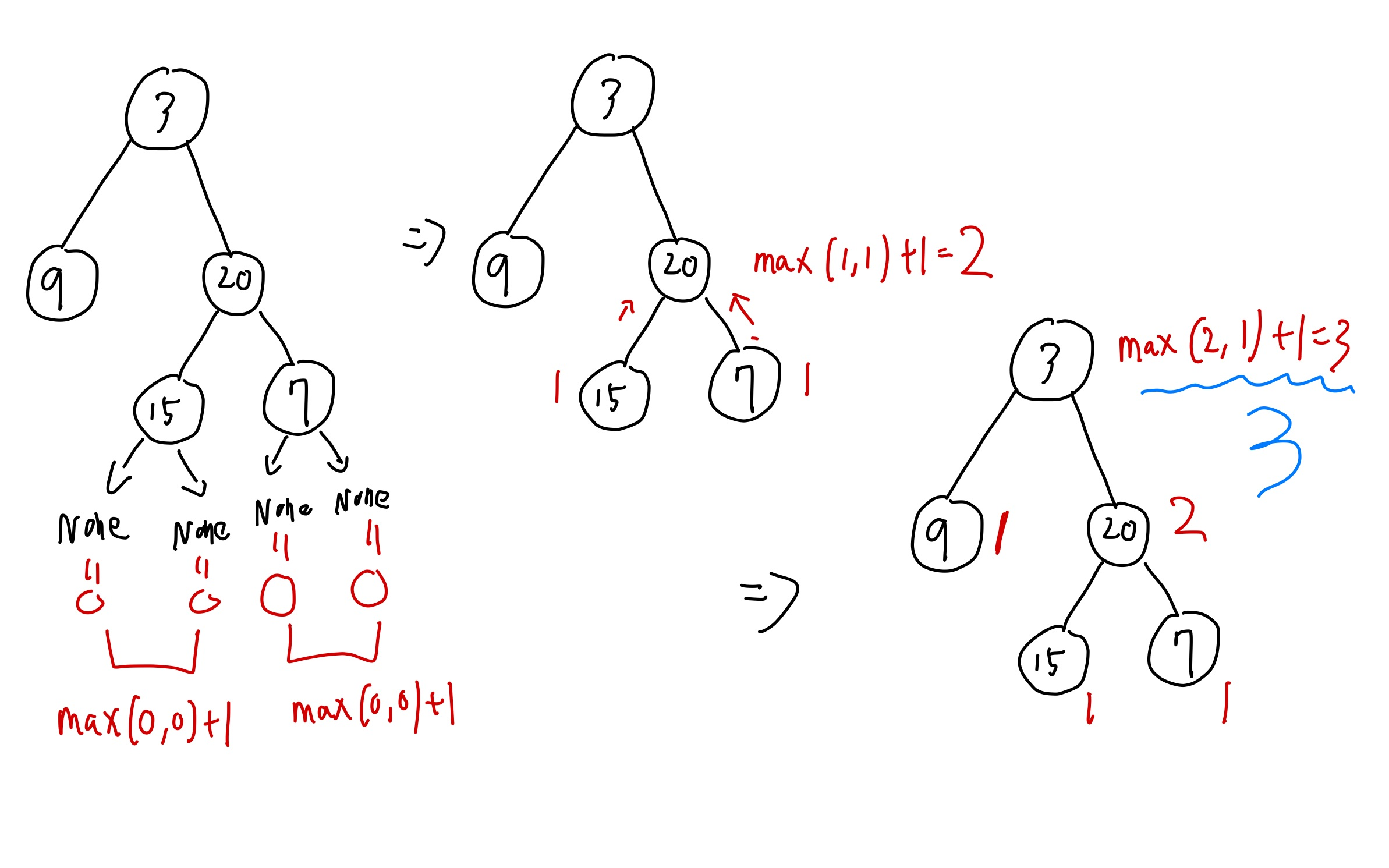
자식 노드들을 보고 자식 노드중에서 큰 값 + 1을 통해 루트 노드를 업데이트 하면서 진행합니다. 이렇게 진행하면 post order traversal을 통해서 구할 수 있습니다.

코드 구현은 아래와 같습니다.

class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution(object):
    # DFS(post-order)
    def maxDepth(self, root):
        """
        :type root: Optional[TreeNode]
        :rtype: int
        """
        if root is None:
            return 0

        left_depth = self.maxDepth(root.left)
        right_depth = self.maxDepth(root.right)
        max_depth = max(left_depth,right_depth) + 1
        return max_depth

코드 설명:

  1. maxDepth 함수는 Post-order traversal를 사용하여 재귀적으로 각 노드의 최대 깊이를 구합니다.
  2. left_depth와 right_depth로 왼쪽과 오른쪽 자식 노드의 깊이를 각각 계산합니다.
  3. 현재 노드의 깊이는 자식 노드 깊이 중 최대값에 1을 더해 계산합니다.
  4. 이렇게 재귀적으로 트리를 순회하며 루트 노드까지 올라오면 최대 깊이를 반환합니다.

시간 복잡도: O(n), 트리의 모든 노드를 방문하므로 노드 수 n에 비례합니다.

결과:

https://leetcode.com/problems/maximum-depth-of-binary-tree/submissions/1451228979

마찬가지로 preorder, inorder로도 구현이 가능합니다.

Preorder

class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution(object):
    def maxDepth(self,root):
        """
        :type root: Optional[TreeNode]
        :rtype: int
        """
        self.max_depth = 0
        
        def pre_order(node, depth):
            if not node:
                return 0
            # Update max depth at each node
            self.max_depth = max(self.max_depth, depth)
            # Traverse the left and right children
            pre_order(node.left, depth + 1)
            pre_order(node.right, depth + 1)
        
        pre_order(root, 1)
        return self.max_depth

코드 설명:

  • 전위 순회를 사용하여 깊이를 업데이트합니다.
  • pre_order 함수를 사용해 노드를 방문할 때마다 현재 깊이와 최대 깊이를 비교하고 self.max_depth를 갱신합니다.
  • 왼쪽, 오른쪽 자식을 재귀적으로 방문하면서 깊이를 1씩 증가시킵니다.

시간복잡도: O(n), 트리의 모든 노드를 방문하므로 n에 비례합니다.

결과:

https://leetcode.com/problems/maximum-depth-of-binary-tree/submissions/1451236505

Inorder

class TreeNode(object):
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution(object):
    def maxDepth(self,root):
        """
        :type root: Optional[TreeNode]
        :rtype: int
        """
        
        self.max_depth = 0
        
        def in_order(node, depth):
            if not node:
                return 0
            
            # Traverse left subtree first
            in_order(node.left, depth + 1)
            
            # Process current node (update depth at the root)
            self.max_depth = max(self.max_depth, depth)
            
            # Traverse right subtree
            in_order(node.right, depth + 1)
        
        in_order(root, 1)
        return self.max_depth

코드 설명:

  • 중위 순회를 사용하여 깊이를 계산합니다.
  • 왼쪽 자식부터 순회하며 깊이를 계산하고, 루트 노드에서 현재 최대 깊이를 업데이트합니다.
  • 오른쪽 자식 노드로 이동하여 동일한 과정을 반복합니다.

시간복잡도: O(n), 트리의 모든 노드를 한 번씩 방문합니다.

결과:

https://leetcode.com/problems/maximum-depth-of-binary-tree/submissions/1451237187

5. 마무리

이번 문제는 이진 트리의 최대 깊이를 찾는 문제로, BFS와 DFS 모두 활용할 수 있는 문제입니다. BFS를 사용하면 레벨 순회 방식을 통해 쉽게 깊이를 계산할 수 있으며, DFS의 다양한 순회 방식을 통해서도 문제를 해결할 수 있습니다. 특히 트리 순회를 통해 깊이를 계산하는 과정을 복습할 수 있었고, 트리의 순회 방식을 바꿔가며 문제의 다양한 풀이 방식을 경험할 수 있었습니다.

트리 문제를 풀 때 다양한 순회 방식에 익숙해지는 것이 중요하며, 이는 트리의 구조를 이해하고 문제를 해결하는 데 큰 도움이 됩니다.

전체 코드는 다음 링크에서 확인할 수 있습니다.

읽어주셔서 감사합니다!!

profile
말하는 감자
할 수 있다
이전 포스트

[LeetCode] 236. Lowest Common Ancestor of a Binary Tree

다음 포스트

[LeetCode] 200. Number of Islands

0개의 댓글