[LeetCode] 236. Lowest Common Ancestor of a Binary Tree

말하는 감자·2024년 11월 12일

DFS binary tree leetcode python tree tree traversal 깊이 우선 탐색 리트코드 이진 트리 코딩테스트 코딩테스트 준비 트리 트리 순회 파이썬

LeetCode

목록 보기

7/32

오늘 문제는 이진 트리에 관한 문제입니다. 한 번 살펴볼까요?

1. 오늘의 학습 키워드

Tree
Binary Tree
Tree Traversal
DFS

2. 문제: 236. Lowest Common Ancestor of a Binary Tree

단계: Medium
주제: Tree, Depth-First Search, Binary Tree
출처: https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-tree/description/

Description

Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.

According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1:

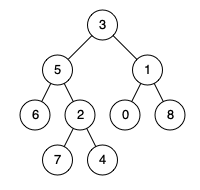
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2:

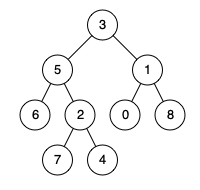
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.

Example 3:

Input: root = [1,2], p = 1, q = 2
Output: 1

Constraints:

The number of nodes in the tree is in the range [2, 105].
$-10^9$ <= Node.val <= $10^9$
All Node.val are unique.
p != q
p and q will exist in the tree.

3. 문제 풀이

Binary 트리 하나와 해당 트리에 속한 두 개의 노드가 주어집니다. 이 때, 두 노드의 공통 조상중 가장 낮은 node 즉, the lowest common ancestor (LCA)를 찾는 문제입니다.

Step1. 문제 이해하기

Input:
- node개수는 2이상 $10^5$ 입니다. 시간복잡도가 $O(n^2)$ 보다 효율적이여야 합니다.
- node값의 크기가 - $10^9$ 이상 $10^9$ 이하 이므로 int형 값을 가진다는 것을 알 수 있습니다.
- node값이 unique하기 때문에 예외 처리를 할 필요가 없습니다.
Output:
- LCA node 값을 출력하면 됩니다.

트리 문제는 보통 트리 구현이나 트리 순회를 활용하는 문제 유형으로 나뉩니다. 따라서 $O(n)$ 의 시간복잡도가 나올것으로 예상됩니다.

Step2. 접근 방법

첫번째 예시를 살펴보겠습니다.

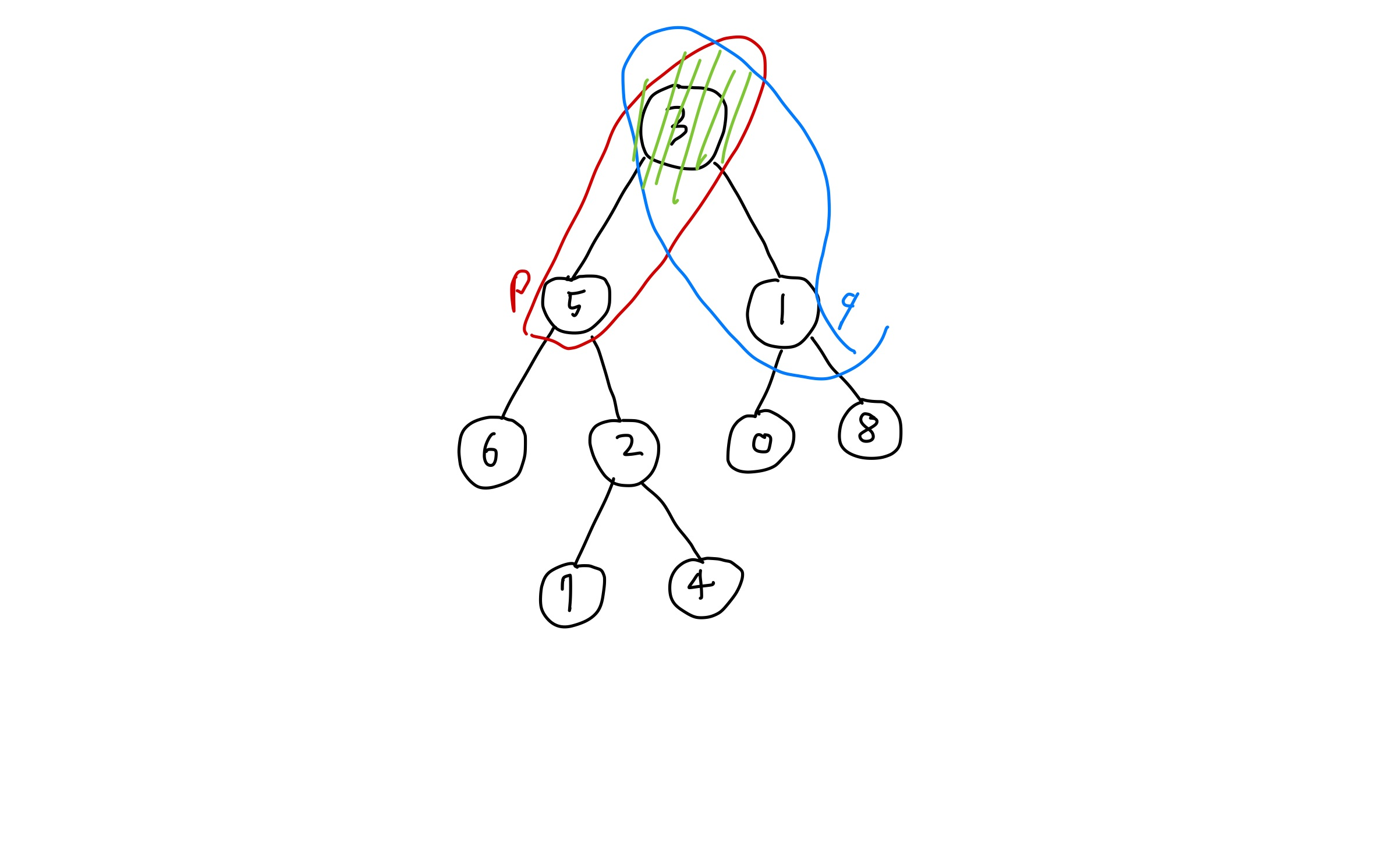
p = 5, q = 1입니다.

공통 조상은 3인것을 알 수 있습니다.

두 번째 예시를 살펴보겠습니다.

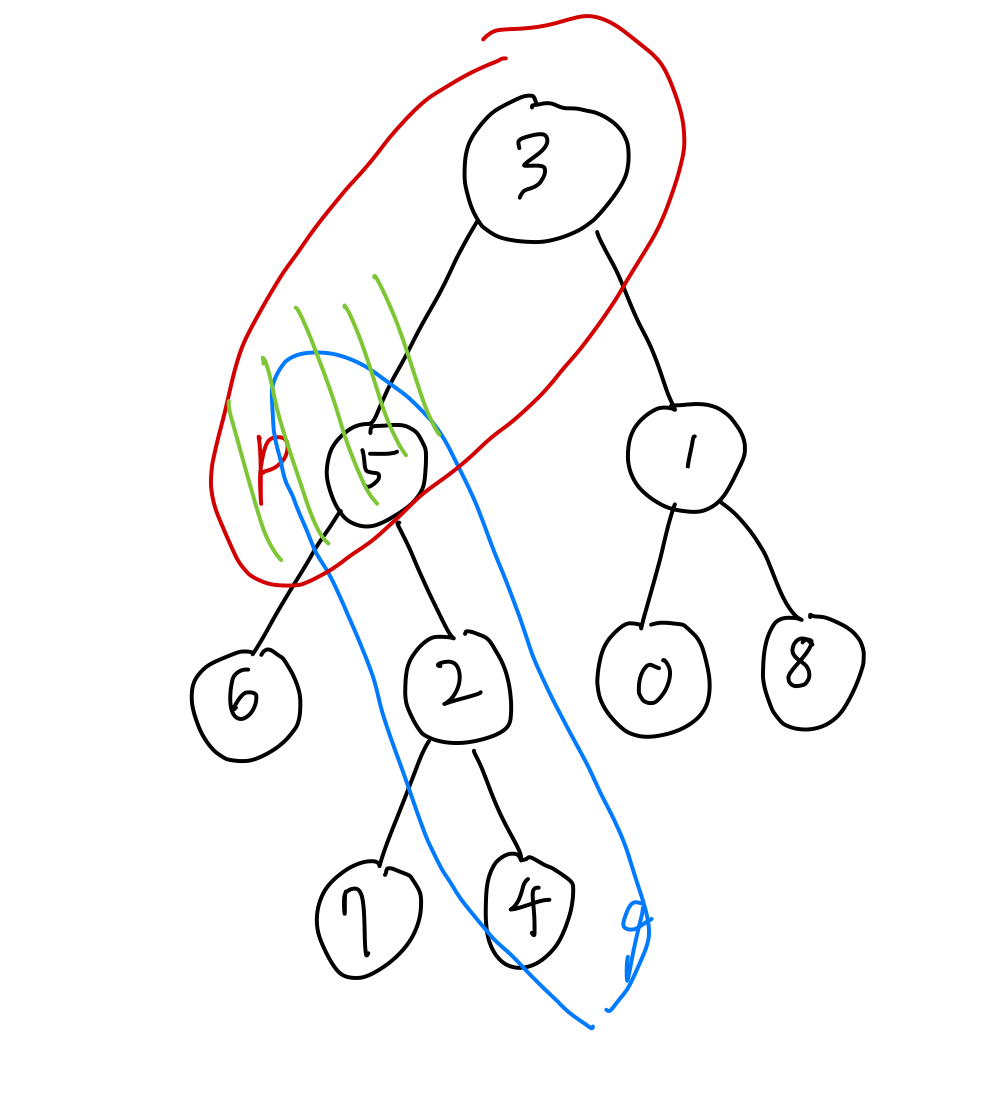
p = 5, q = 4입니다.

LCA는 5입니다.

또 다른 예시를 보겠습니다.

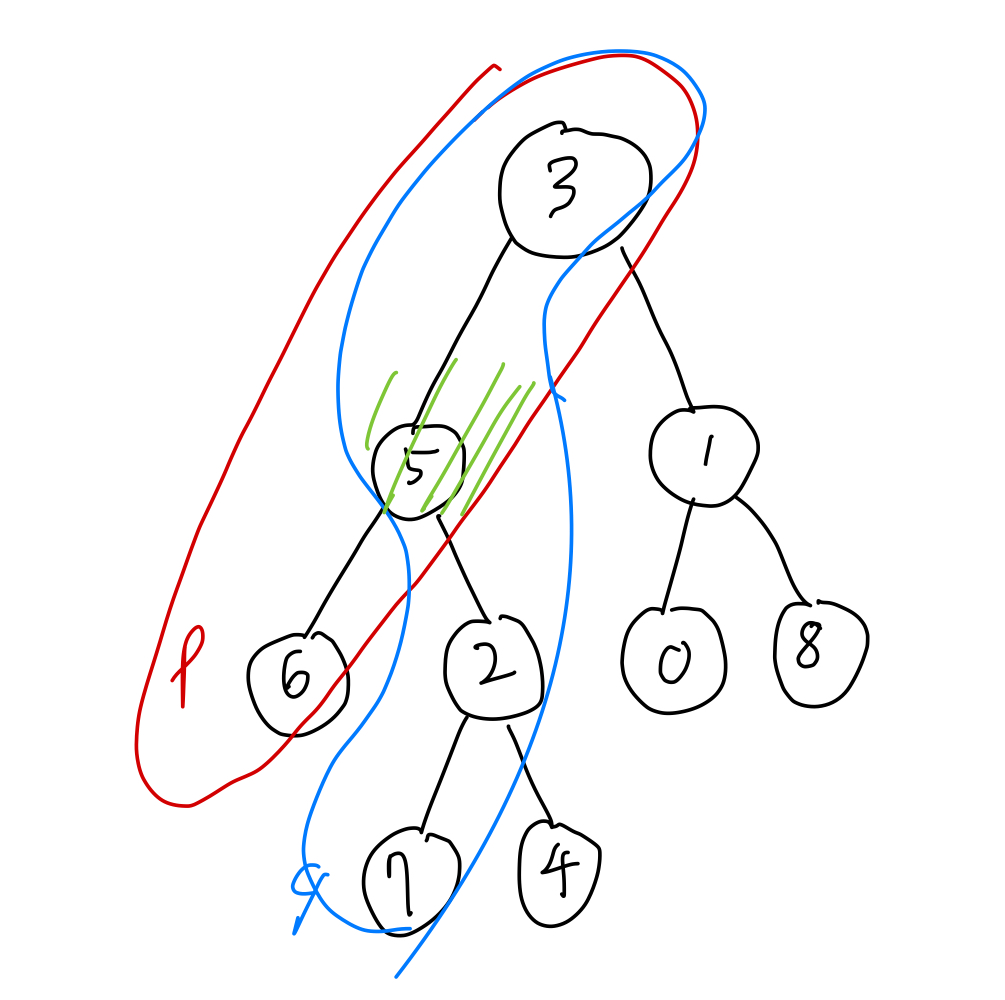
p = 6, q = 7, LCA = 5입니다.

이와 같이 여러 예시를 통해 공통 조상을 찾는 문제의 핵심 아이디어를 파악할 수 있습니다.

LCA를 찾기 위해 루트에서 자식 노드로 내려가며 탐색해야 합니다. 이 과정에서 자식 노드 중 하나라도 p 또는 q를 포함하면 해당 노드가 LCA 후보가 됩니다. 이를 통해 다음의 조건을 도출할 수 있습니다:

왼쪽, 오른쪽 자식 모두에서 p와 q 중 하나씩 발견되면 현재 노드가 공통 조상(LCA)입니다.
현재 노드가 p나 q 중 하나일 경우, 해당 노드를 그대로 반환합니다. 자식 노드에 p 또는 q가 없는 경우 LCA가 아닙니다.
한쪽 자식 노드에서만 p 또는 q를 찾은 경우에는 그 자식을 반환합니다. 이는 그 자식이 최종 LCA라는 뜻입니다.

Step3. 코드 설계

트리 순회를 통해 위의 조건을 효율적으로 확인할 수 있습니다. 후위 순회(DFS) 방식으로 트리를 탐색하며 조건을 검사하면 됩니다.

재귀 탐색을 이용해 자식 노드들을 먼저 확인합니다. 각 노드에서 왼쪽과 오른쪽 자식 노드로 재귀적으로 이동하여 p와 q를 찾습니다.
현재 노드가 p 또는 q일 경우 해당 노드를 반환합니다.
양쪽 자식 노드에서 모두 값을 반환받은 경우 현재 노드가 p와 q의 가장 낮은 공통 조상이 됩니다.
한쪽 자식 노드에서만 값을 받는다면 해당 노드가 LCA로 확정됩니다.

이 접근 방식으로 문제를 해결하면 시간 복잡도는 O(n)이 될 것으로 예상되며, 각 노드를 한 번씩만 방문하게 됩니다.

Step4. 코드 구현

# Definition for a binary tree node.
class TreeNode(object):
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        if root is None:
            return None
        left = self.lowestCommonAncestor(root.left,p,q)
        right = self.lowestCommonAncestor(root.right,p,q)
    
        if root.val == p.val or root.val == q.val:
            return root
        elif left and right:
            return root
        
        return left or right

코드 설명:

위의 코드는 재귀적으로 트리를 탐색하여 두 노드 p와 q의 가장 낮은 공통 조상(LCA)을 찾는 방식으로 작성되었습니다. 각 노드에서 다음과 같은 단계로 LCA를 탐색합니다:

base 조건: 현재 노드가 None이면 None을 반환합니다.
현재 노드가 p 또는 q인 경우: 현재 노드가 p 또는 q와 일치하면 해당 노드를 반환합니다. 이는 현재 노드가 공통 조상의 후보가 될 수 있음을 의미합니다.
좌우 자식 노드에서 탐색: 왼쪽 자식과 오른쪽 자식 노드에서 각각 lowestCommonAncestor 재귀 호출을 수행합니다.
- left와 right 변수는 각각 왼쪽과 오른쪽에서 반환된 결과를 저장합니다.
LCA 판별:
- 만약 left와 right가 모두 None이 아닌 경우, 즉, 두 자식 노드에서 각각 p와 q가 발견되었다면 현재 노드가 가장 낮은 공통 조상이므로, 현재 노드를 반환합니다.
- 만약 한쪽에서만 값을 반환받았다면, 그쪽 노드가 p와 q의 공통 조상(LCA)이 될 수 있습니다. 따라서 left 또는 right 값을 반환합니다.
LCA 반환: 루트부터 시작해 재귀적으로 탐색하여 최종적으로 LCA 노드를 반환합니다.