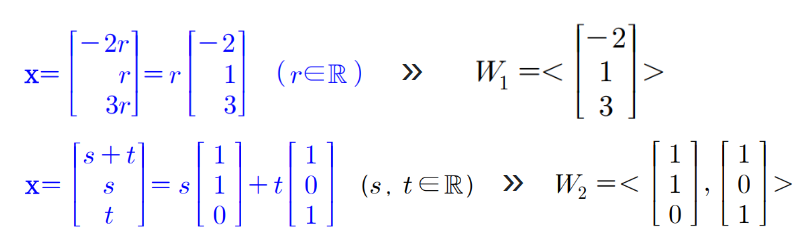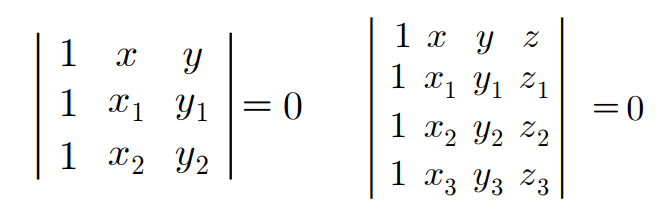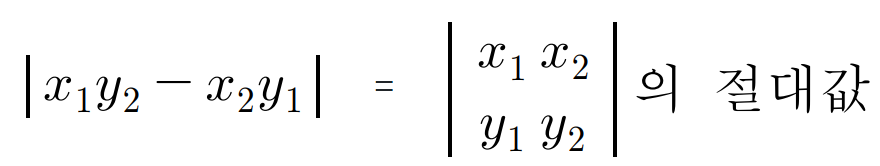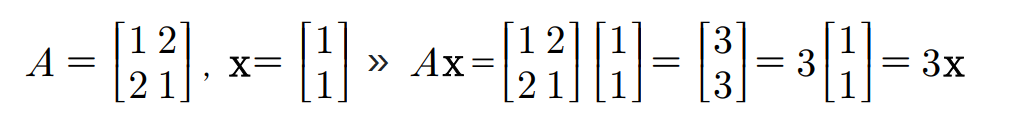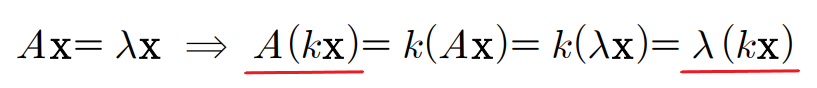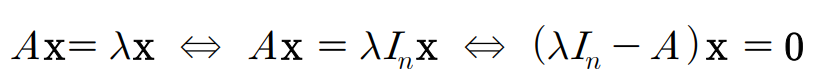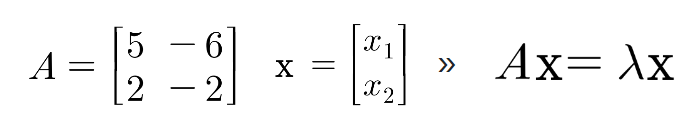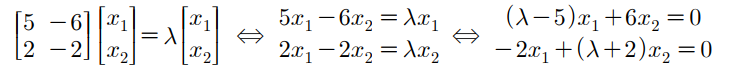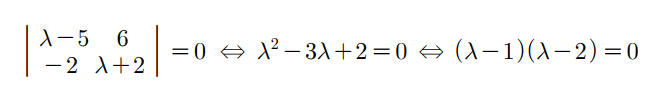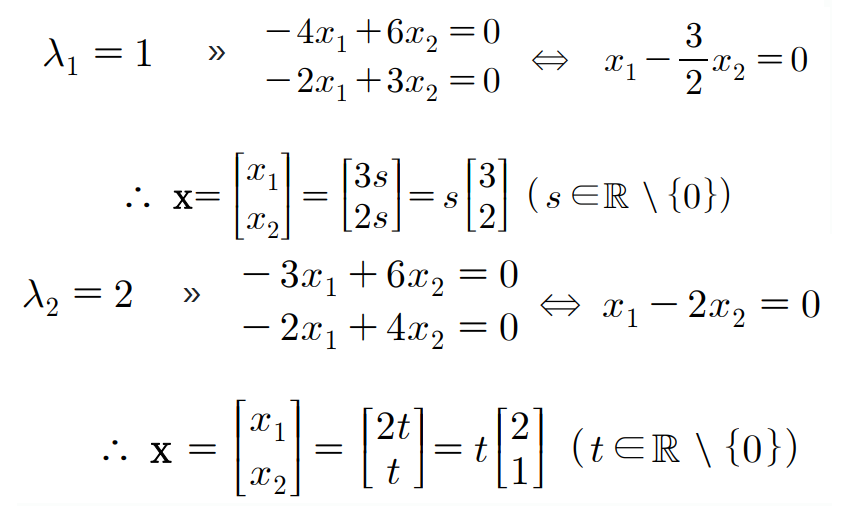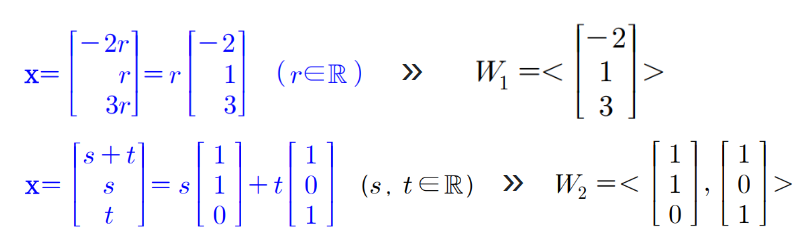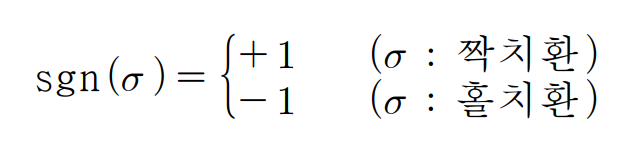네이버 부스트캠프 AI Tech 4기 선형대수학 스터디 3회차
선형대수학 이상구 저 Chapter4
4.1 행렬식의 정의와 기본정리
정의 [치환]
- 자연수의 집합 S={1, 2, …, n}의 치환(permutation, 순열)은 S에서 S로의 일대일대응함수
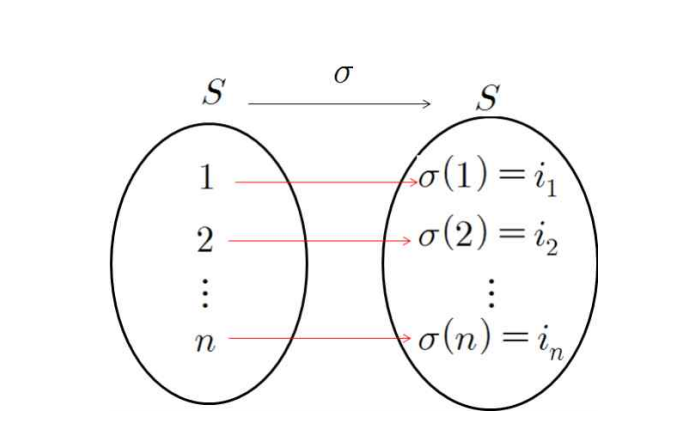
- 치환을 간단히, σ=(σ(1) σ(2) ⋯ σ(n))=(i1 i2 ⋯ in)
- 이는 일대일대응이므로 사실상 1, 2, …, n을 일렬로 배열하는 것과 같을 것
- 따라서 S={1, 2, …, n}의 치환은 n!가지. 1부터 n을 배열하는 것이니까.
- S의 모든 치환 집합 n!개를 Sn으로 표시
- 반전(inversion)
- 치환 (j1 j2 ⋯ jn)에서 큰 자연수가 작은 자연수보다 더 왼쪽에 나타나도록 치환된 경우를 의미
- jk에 대한 반전의 개수
- k번째 수인 jk에서 반전이 일어났을 때, jk보다 작으면서 k+1번째 이후로 나타나는 수의 개수를 jk에 대한 반전수라고 함
- 치환 (j1 j2 ⋯ jn)의 반전수란 각각의 jk에 대한 반전수를 모두 더한 것
정의 [짝치환과 홀치환]
- 치환이 가진 반전의 총 개수가 짝수이면 짝치환(even permutation), 홀수이면 홀치환(odd permutation)
정의 [부호화 함수]
- Sn의 각 치환을 +1 또는 −1이라는 수에 대응시키는 부호화 함수(signature function) sgn : Sn→{+1, −1}
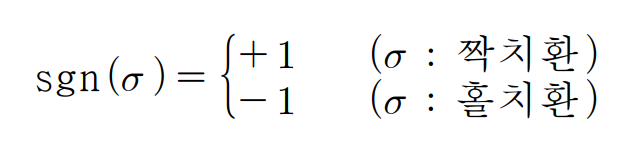
- 예시
치환하여 (1 4 2 3)이면, 4에서 반전 2개(2, 3), 나머지는 크기 순서대로 정렬되었으므로 반전의 총 개수는 2개, 짝치환이고 부호화 함수에 따라 + 부호
- 만약 치환 σ 안에서 임의의 두 수 자리를 바꾼 치환을 τ라고 하면 아래 식을 만족
sgn(τ)=−sgn(σ)
- 임의의 두 수 자리를 바꾸면 치환의 개수가 1개 늘거나 줄어서 부호가 바뀜
정의 [행렬식][Leibniz formula]
- 행렬 A=[aij]가 n차 정사각행렬일 때, A의 행렬식을 det(A) 또는 ∣A∣로 나타냄
det(A)=∑σ∈Snsgn(σ)a1σ(1)a2σ(2) ⋯ anσ(n)
- 1차 정사각행렬 A=[a]라면 행렬식은 det(A)=a
- 2차 정사각행렬 A라면, 크기는 2×2이고 S2={σ1, σ2}={(1 2), (2 1)}
- 2차이므로 2가지의 치환집합을 가지는 것 {(1 2), (2 1)}
- sgn(σ1)=1, sgn(σ2)=−1
- det(A)=sgn(σ1)a1σ1(1)a2σ1(2)+sgn(σ2)a1σ2(1)a2σ2(2)=a11a22−a12a21
- det(A)를 구하는 것은 행렬식을 계산해 ∣A∣를 구하라는 것과 같은 의미
- det를 계산하는 이상하게 복잡한 식이 우변처럼 간단해짐(Sarrus 방법)
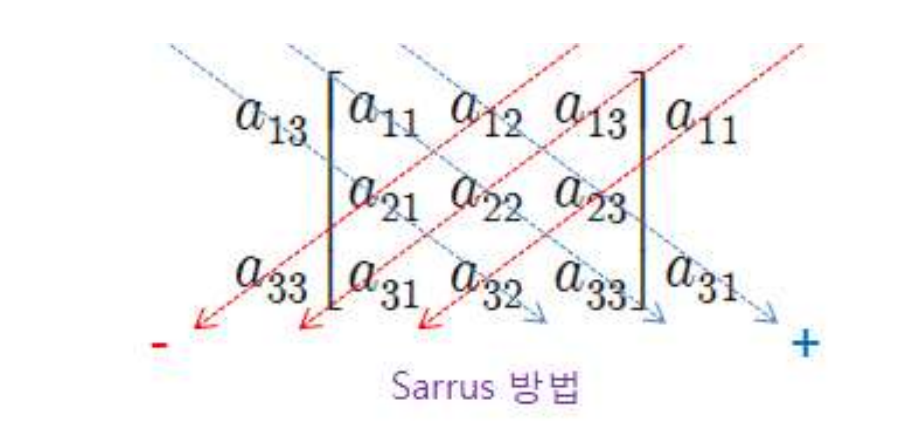
- 4차 이상의 행렬식에서는 적용할 수 없음
- 하지만 정의로 이를 구하는 것도 계산량이 어마어마하므로 불가능
- 행렬식의 성질을 이용하자!
행렬식의 성질
- 정사각행렬 A의 행렬식과 A의 전치행렬 AT의 행렬식의 값은동일
- 행렬 B가 정사각행렬 A의 두 행(열)을 서로 바꾸어 얻어진 행렬이라면 ∣B∣=−∣A∣
- 행에 관한 행렬식의 성질이 열에 관해서도 모두 성립
- 정사각행렬 A의 두 행(열)이 일치하면 ∣A∣=0
- 정사각행렬 A의 한 행(열)의 성분이 모두 0이면 ∣A∣=0
- 정사각행렬 A의 한 행을 k배하여 얻은 행렬을 B라 하면 ∣B∣=k∣A∣
- 정사각행렬 A의 두 행이 비례하면 ∣A∣=0
- 정사각행렬 A의 한 행의 k배를 다른 행에 더해 얻은 행렬을 B라 하면 ∣B∣=∣A∣
- A=[aij]가 n차의 삼각행렬이면 A의 행렬식은 주대각선성분의 곱과 같음
- ∣A∣=a11a22 ⋯ ann
- 오른쪽 위를 채우는 직각삼각형 모양이라면 빗변의 숫자만 모두 곱한 값이란 뜻
- E가 n차의 기본행렬(Elementary matrix)이면 det(EA)=det(E)det(A)
- 기본행렬에 관한 행렬식은 아래 참조

- A가 가역행렬일 필요충분조건은 detA=0
- 두 행렬 A, B가 n차의 정사각행렬이면 ∣AB∣=∣A∣∣B∣ 성립
- 행렬 A가 가역이면 ∣A∣=0, ∣A−1∣=∣A∣1 성립
- 행렬식을 계산하는 방법
- 기본행연산을 활용, 행렬식의 한 행(열)에 0이 많이 나타나도록 함
- 대각선 성분을 곱함
- 상수배를 하는 경우와 행을 교환하는 경우에 다시 1/k배, −1배를 한다는 것 주의
4.4 행렬식의 응용
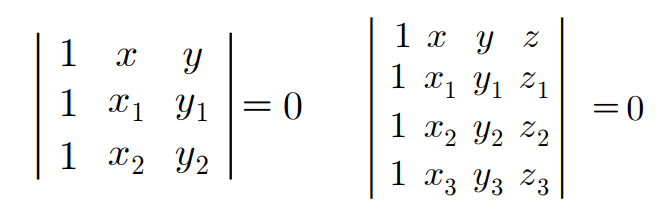
- 평행사변형은 두 벡터를 이용해 표현할 수 있고, 이는 넓이 계산 식으로 이어짐
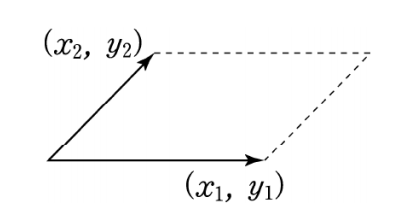
- 평행사변형 넓이∣x1y2−x2y1∣는 아래와 같이 해석됨
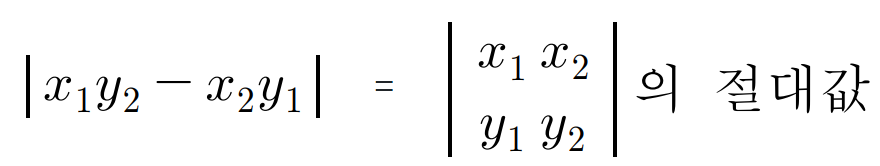
- 여기서 파생되어 부피 계산으로 이어짐
- 평행 육면체는 세 개의 벡터로 생성, 이들을 열벡터로 가지는 행렬 A의 부피도 det(A)의 절댓값
- 넓이를 다르게 표현하면 두 벡터 u,v에 대해 detATA
- 증명은 생략, detATA=∣∣u∣∣2∣∣v∣∣2sin2θ 이는 밑변과 높이를 곱한 값의 제곱이므로 루트를 씌워 넓이로 해석
- Vandermonde 행렬은 위와 같은 맥락으로, 어떤 점들을 지나는 그래프의 넓이를 행렬로 구할 수 있게 함
4.5 고유값과 고유벡터
정의 [고유값과 고유벡터]
- A는 n차의 정사각행렬. 0아닌 벡터 x∈Rn가 적당한 스칼라 λ에 대하여 다음을 만족하면 λ를 A의 고유값(eigenvalue)이라 하고, x를 λ에 대응하는 A의 고유벡터(eigenvector)라고 함
Ax=λx
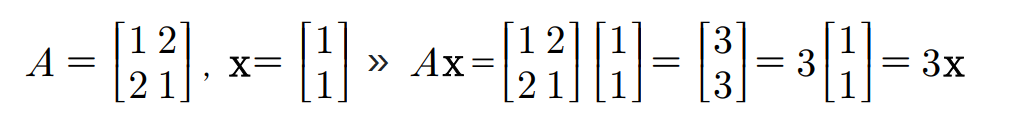
- 위와 같은 경우, 고유값은 3, 이에 대응하는 고유벡터는 x
- x∈Rn에 대해 Inx=1x이므로 항등행렬 In의 교유값은 λ=1 하나, x∈Rn는 이 λ에 대응하는 In의 고유벡터
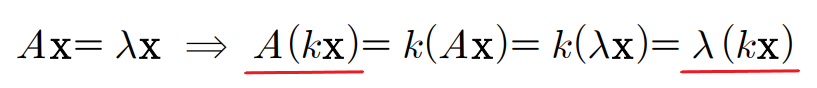
- 위 예시처럼 0이 아닌 임의의 스칼라 k에 대해 kx도 λ에 대응하는 A의 고유벡터
고유값을 구하는 일반적인 방법
고유값이 뭔지는 알았는데, 어떻게 구할까?
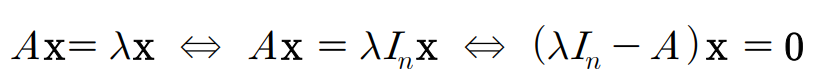
-
여기서 (λIn−A)x=0은 0이 아닌 해를 가져야 함. 그렇다면, 특성방정식(characteristic equation) ∣λIn−A∣=0가 성립해야 한다는 의미. fA(λ)=∣λI−A∣는 특성다항식(characteristic polynomial)
-
정리해보자면, A가 n×n 행렬, λ가 스칼라이면 아래 명제는 동치
- λ는 A의 고유값
- λ는 특성방정식 det(λIn−A)=0의 해
- det(λIn−A)와 ∣λIn−A∣는 동일한 의미라는 것을 배웠음
- 동차선형연립방정식 (λIn−A)x=0은 자명하지 않은 해도 가짐
- x가 영벡터 이외의 해를 가진다는 의미
-
예제 3번
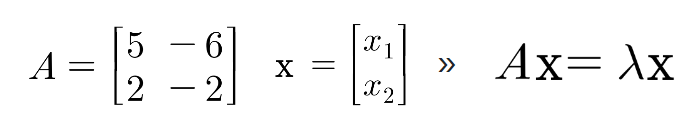
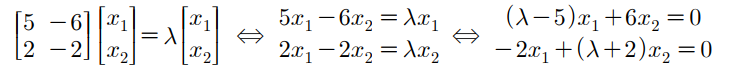
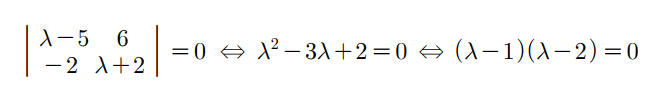
- 최종적으로 λ가 1일 때, 2일 때의 고유벡터 x가 다름
- A는 2차 정사각행렬이므로 2개의 고유값을 가지는 것
- 이때, x1−2x2=0을 풀어야 하는데, 각각 2t,t 실수로 설정
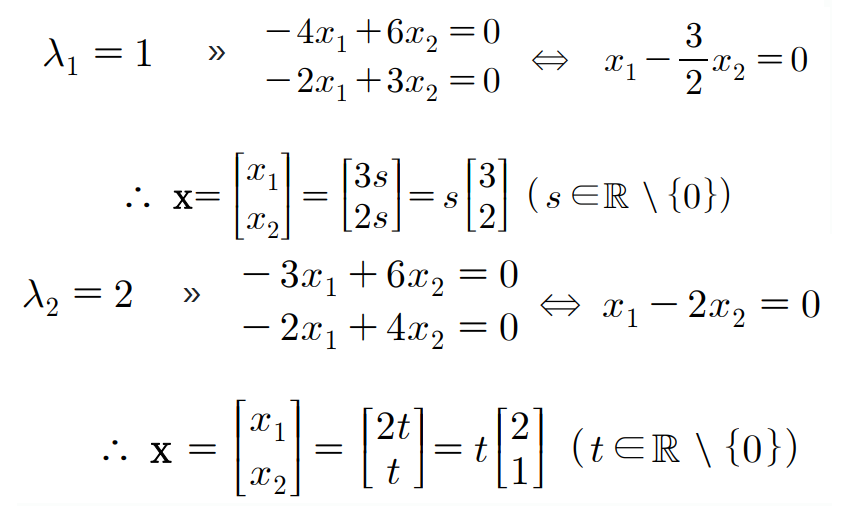
- 대수학의 기본 정리
실수(혹은 복소수) 계수를 갖는 모든 n차 다항식p(x)=anxn+an−1xn−1+⋯+a1x+a0 은 복소평면에서 p(x)=0을 만족하는 n개의 근 x1,x2,…,xn을 가짐
- 이는 n차 정사각실수행렬 A의 n개 고유값은 복소수 범위에서 항상 존재한다는 뜻
- 스칼라를 실수로 제한하는 경우에는 없을 수도 있다는 것
- 실수 범위에서 없다는 의미이지, 복소수(허수) 범위에서는 반드시 존재
- 삼각행렬 T의 모든 고유값은 T의 주대각선성분인 t11,t22,…,tnn
- n차 삼각행렬 T=[tij]에 대해 λI−T의 주대각선성분은 λ−tii(i=1,…,n)
- 그럼 T의 특성다항식 det(λI−A)=(λ−t11)(λ−t22)⋯(λ−tnn)=0
- 왜? Sarrus 방법에서 대각선 곱이 아니라면 모두 0이 포함되므로 대각선만 남게 됨
정의 [고유공간(eigenspace)]
- λ가 n차의 정사각행렬 A의 고유값일 때, 동차연립방정식 (λIn−A)x=0의 해공간을 λ에 대응하는 A의 고유공간(eigenspace)이라 함
- 다시말해 λ에 대응하는 A의 고유공간은 고유벡터 전체와 영벡터로 이루어진 집합
- 고유값 λ에 대응하는 고유공간은 다음과 같이 표현 가능
- 공간의 개념은 W=<S>, S 집합의 원소들의 일차결합으로 만든 공간 W였음
- 아래와 같이 고유값에 대응하는 고유벡터로부터 고유공간을 쓸 수 있음