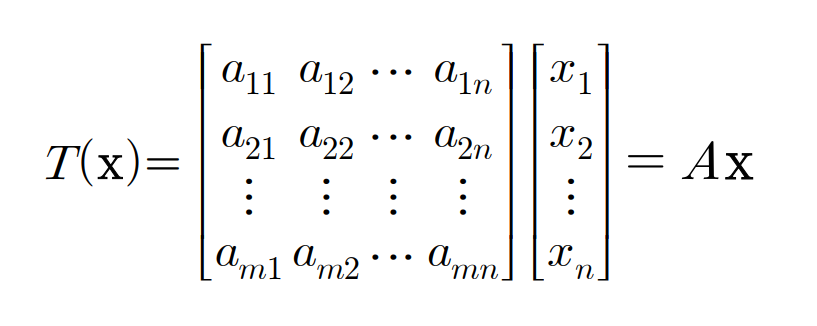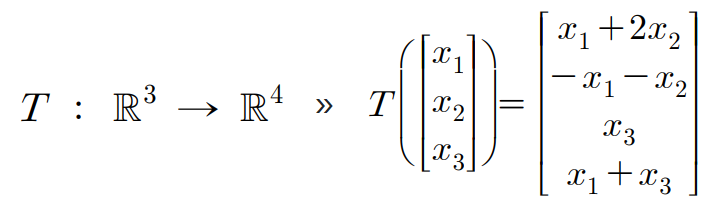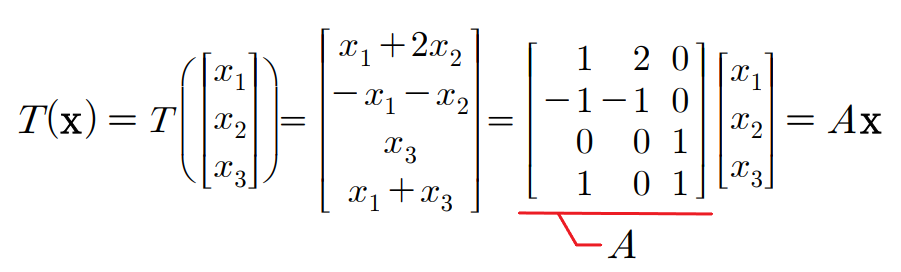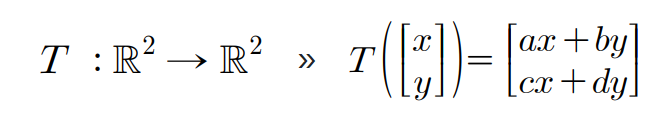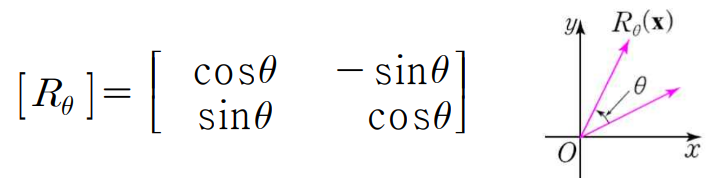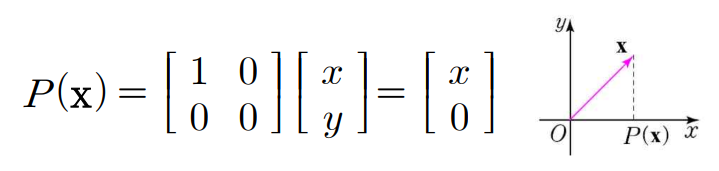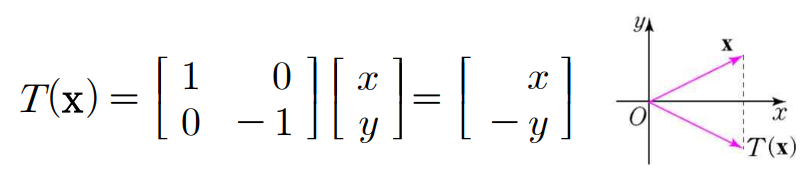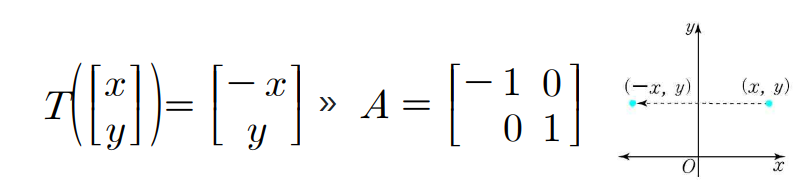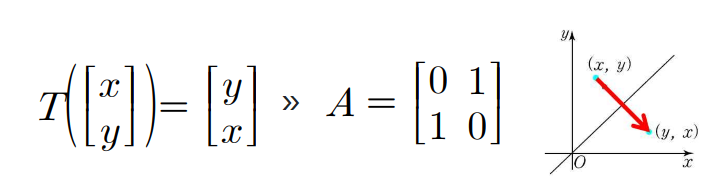네이버 부스트캠프 AI Tech 4기 선형대수학 스터디 4회차
선형대수학 이상구 저 Chapter6
지금까지는 행렬을 선형연립방정식과 관련된 계수행렬로 생각했지만 행렬을 함수 로 생각해보면 어떨까? 부분공간 사이에서 연산을 보존한다는 의미를 갖는 함수인 선형변환 으로 생각해보자! 차원이 다른 두 공간에서 선형변환은 언제나 행렬로 나타내는 것이 가능 하다. 그럼 선형변환은 어떤 기하학적 의미를 가지는지 알아보자.
6.1 함수(변환)로서의 행렬
정의 [변환]
입력과 출력이 모두 벡터인 함수를 변환(Transformation) 이라 함. 그럼 공간 R n \mathbb{R}^n R n R m \mathbb{R}^m R m T : R n → R m T : \mathbb{R}^n \rightarrow \mathbb{R}^m T : R n → R m w = T ( x ) \mathbf{w} = T(\mathbf{x}) w = T ( x ) x \mathbf{x} x T T T 이미지(image) , x \mathbf{x} x w \mathbf{w} w 원상(pre-image) 이라 함.
행렬 A A A m × n m \times n m × n T A ( x ) = A x , x ∈ R n T_A(\mathbf{x}) = A\mathbf{x}, \mathbf{x} \in \mathbb{R}^n T A ( x ) = A x , x ∈ R n T : R n → R m T : \mathbb{R}^n \rightarrow \mathbb{R}^m T : R n → R m 행렬변환(matrix transformation) 이라 함.
pre-image x \mathbf{x} x T T T w \mathbf{w} w 변환을 행렬로 한다면 행렬변환
정의 [선형변환]
R n \mathbb{R}^n R n R m \mathbb{R}^m R m T : R n → R m T : \mathbb{R}^n \rightarrow \mathbb{R}^m T : R n → R m u , v ∈ R n \mathbf{u}, \mathbf{v} \in \mathbb{R}^n u , v ∈ R n k k k T T T R n \mathbb{R}^n R n R m \mathbb{R}^m R m 선형변환(linear transformation) 이라 함T ( u + v ) = T ( u ) + T ( v ) T(\mathbf{u} + \mathbf{v}) = T(\mathbf{u}) + T(\mathbf{v}) T ( u + v ) = T ( u ) + T ( v ) T ( k u ) = k T ( u ) ( k ∈ R ) T(k\mathbf{u}) = kT(\mathbf{u})\ \ \ \ \ (k \in \mathbb{R}) T ( k u ) = k T ( u ) ( k ∈ R )
이는 선형 이라는 이름에 맞는 특징. 선형적인 일차함수 위의 두 점에서도 성립하는 성질
R n \mathbb{R}^n R n R n \mathbb{R}^n R n R n \mathbb{R}^n R n 선형연산자(linear operator) 라 함
예제 1, 2에서와 같이 T T T
T ( x , y , z ) = ( x , y ) T(x,y,z) = (x,y) T ( x , y , z ) = ( x , y ) R 2 \mathbb{R}^2 R 2 x y xy x y 정사영(orthogonal projection) 이라 함
특수한 선형변환
만약 T : R n → R m T : \mathbb{R}^n \rightarrow \mathbb{R}^m T : R n → R m T ( 0 ) = 0 T(\mathbf{0}) = \mathbf{0} T ( 0 ) = 0 T ( − v ) = − T ( v ) T(-\mathbf{v}) = -T(\mathbf{v}) T ( − v ) = − T ( v ) T ( u − v ) = T ( u ) − T ( v ) T(\mathbf{u} - \mathbf{v}) = T(\mathbf{u}) - T(\mathbf{v}) T ( u − v ) = T ( u ) − T ( v )
이들의 증명은 선형변환의 특징 2가지를 고루 사용
R n \mathbb{R}^n R n R m \mathbb{R}^m R m 모든 선형변환은 행렬변환으로 나타낼 수 있음
증명 과정은 생략, 그냥 그렇다고만 알고 있으면 될 듯
행렬 A = [ a i j ] m × n A = [a_{ij}]_{m \times n} A = [ a i j ] m × n T T T 표준행렬(standard matrix) 라 하고, [ T ] [T] [ T ]
T : R n → R m T : \mathbb{R}^n \rightarrow \mathbb{R}^m T : R n → R m T T T A = [ T ] A = [T] A = [ T ] x ∈ R n \mathbf{x} \in \mathbb{R}^n x ∈ R n T ( x ) = A x T(\mathbf{x}) = A\mathbf{x} T ( x ) = A x A = [ T ( e 1 ) : T ( e 2 ) : ⋯ : T ( e n ) ] A = [T(\mathbf{e}_1) : T(\mathbf{e}_2) : \dots : T(\mathbf{e}_n)] A = [ T ( e 1 ) : T ( e 2 ) : ⋯ : T ( e n ) ]
예제 6. 아래와 같은 선형변환을 T ( x ) = A x T(\mathbf{x}) = A\mathbf{x} T ( x ) = A x
A A A
결국 요약하면 변환 T T T 어떤 한 공간의 벡터를 다른(혹은 같은) 공간의 벡터로 바꿀 수 있는 함수 역할인데, 그 중 선형적인 성질을 가지는 선형변환 이 존재하며 모든 선형변환은 행렬로 표현 할 수 있다는 것!
6.2 선형변환의 기하학적 의미
선형변환이 위와 같이 정의된다면, O P → = ( x , y ) \overrightarrow{OP} = (x, y) O P = ( x , y ) T T T O Q → = ( a x + b y , c x + d y ) \overrightarrow{OQ} = (ax + by, cx + dy) O Q = ( a x + b y , c x + d y )
회전 선형변환
R 2 → R 2 \mathbb{R}^2 \rightarrow \mathbb{R}^2 R 2 → R 2 θ \theta θ 옮겨진 점의 좌표를 삼각함수로 나타낸 후 덧셈공식을 사용해 풀면 아래와 같은 R θ R_\theta R θ
x x x
R 2 → R 2 \mathbb{R}^2 \rightarrow \mathbb{R}^2 R 2 → R 2
x x x
R 2 → R 2 \mathbb{R}^2 \rightarrow \mathbb{R}^2 R 2 → R 2
(예제 2) y y y A A A
(예제 2) y = x y = x y = x A A A
변환하여 어느 점에 있을지 기하적으로 생각해보고, 그 점을 표현하기 위한 식을 쓰자
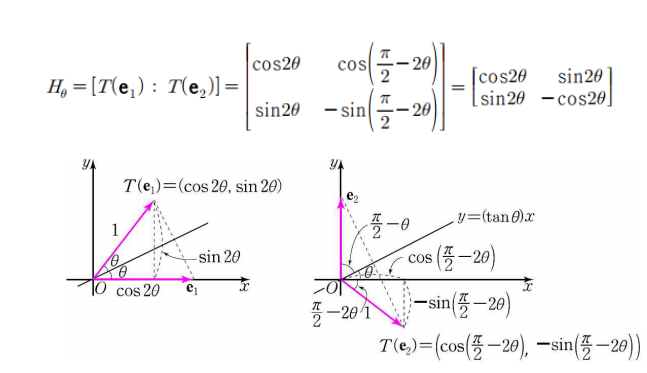
(예제 3) x x x θ \theta θ H θ = [ T ( e 1 ) : T ( e 2 ) ] H_\theta = [T(e_1) : T(e_2)] H θ = [ T ( e 1 ) : T ( e 2 ) ]