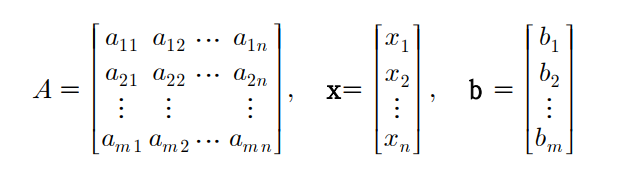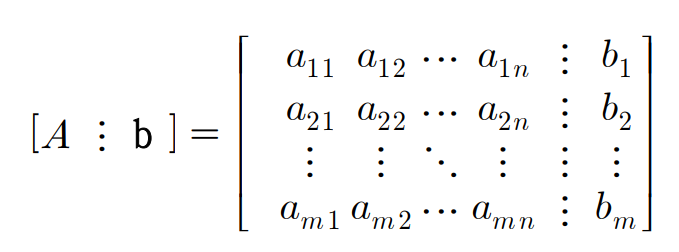Chapter2. 선형연립방정식

장원준·2022년 11월 5일

선형대수학

목록 보기

2/9

네이버 부스트캠프 AI Tech 4기 선형대수학 스터디 2회차

선형대수학 이상구 저 Chapter2

2.1 선형연립방정식

정의 [선형방정식]

미지수 $x_1,\ x_2,\ ...,\ x_n$ 에 관한 선형방정식(linear equation)은 아래와 같은 모양 $a_1x_1 + a_2x_2 + \dots + a_nx_n = b$

$b$ 와 $a_1,\ a_2,\ ...,\ a_n$ 는 실수

미지수 $x$ 의 차수가 1인 일차식과 상수항( $b$ )으로 이루어진 방정식

$\sqrt{x},\ \mathrm{sin}{x}$ 등이 포함되면 선형방정식이 아님

정의 [선형연립방정식]

아래와 같이 미지수 $x_1,\ x_2,\ ...,\ x_n$ 에 관한 유한 개의 선형방정식 모임을 선형연립방정식(system of linear equations), 상수항 $b_1,\ b_2,\ ...,\ b_m$ 이 모두 0일 경우 동차선형연립방정식(homogeneous system of linear equations, 동차선형방정식시스템) $a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1$ $a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2$ $\vdots$ $a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m$

정의 [선형연립방정식의 해]

선형연립방정식의 미지수 $x_1,\ x_2,\ ...,\ x_n$ 에 어떤 수 $s_1,\ s_2,\ ...,\ s_n$ 을 대입했을 때 각 방정식이 모두 성립한다면 ( $s_1,\ s_2,\ ...,\ s_n$ )이 해(solution)

해가 존재하면 consistent, 해가 존재하지 않으면 inconsistent

해 전체의 집합을 해집합(solution set), 동일한 해집합을 가지는 두 선형연립방정식을 동치(equivalent)라고 함

미지수가 2개인 2개의 선형연립방정식은 아래 중 하나만을 만족
- 유일한 해를 가짐
- 무수히 많은 해를 가짐
- 해를 갖지 않음
  » 두 개의 일차방정식(직선)이 존재한다고 볼 수 있는데, 그렇다면 두 직선이 가질 수 있는 관계는 위 세 개뿐이기 때문
미지수가 3개인 3개의 선형연립방정식은 세 개의 평면이 존재한다고 볼 수 있음
- 세 평면이 동시에 겹치는 부분이 있다면, 그것이 해
- 따라서 한 점일수도, 무수히 많을수도(교선을 형성한다면), 없을 수도 있음
미지수가 5개인 3개의 선형연립방정식은 남는 2개의 미지수에 임의의 실수를 부여하여 풀이
- 미지수가 방정식보다 많은 경우에 대한 일반적인 해법
- $x_1 = s,\ x_2 = t$ 와 같이 임의의 실수로 설정
  - 2.2장 마지막에 나올 선형연립방정식의 RREF에 따라 실수로 설정하기 좋은 변수를 알 수 있음
- 이에 대해 $x_3,\ x_4,\ x_5$ 도 $s,\ t$ 로 표현이 가능

정의 [행렬]

실수나 복소수를 직사각형 모양의 행과 열로 배열한 것을 행렬(matrix), 그 각각의 수를 행렬의 성분(entry)라고 함

행렬 $A$ 에서 가로 $i$ 번째 줄을 $i$ 행( $i$ -th row of $A$ )

행렬 $A$ 에서 세로 $j$ 번째 줄을 $j$ 열( $j$ -th column of $A$ )

$m$ 개의 행과 $n$ 개의 열을 갖는 행렬 $A$ 의 크기(size)는 $m \times n$

$m = n$ 이면 $n$ 차의 정사각행렬(square matrix)

$m = n =1$ 이면 보통 $A = [2] = 2$ 로 작성

$A_{(i)}$ 는 $A$ 의 $i$ 번째 행
$A^{(j)}$ 는 $A$ 의 $j$ 번째 열
행렬 $A$ 의 $i$ 행, $j$ 열의 성분 $a_{ij}$ 를 $A$ 의 $(i,\ j)$ 성분이라 함
$n$ 차의 정사각행렬 $A$ 의 성분 $a_{11},\ a_{22},\ ...,\ a_{nn}$ 을 주대각선성분(main diagonal entries)라고 함
- 주대각선성분은 기호로 $d_{11},\ d_{22},\ d_{33}$ 으로 표현
$m$ 행, $n$ 열의 행렬 $A$ 를 $(i,\ j)$ 성분을 사용하여 아래와 같이 간소화하는 것이 가능 $A = [a_{ij}]_{m \times n}\ \ \ \ \ \ \ \ \ or\ \ \ \ \ \ \ \ \ A = [a_{ij}]$

정의 [선형연립방정식의 계수행렬과 첨가행렬]

$n$ 개의 미지수를 갖는 $m$ 개의 일차방정식으로 이루어진 선형연립방정식에 대해 아래와 같이 $A,\ \mathrm{x},\ \mathrm{b}$ 로 나타내는 것이 가능 $a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1$ $a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2$ $\vdots$ $a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m$

$A\mathrm{x} = \mathrm{b}$

여기서 행렬 $A$ 를 선형연립방정식의 계수행렬(coefficient matrix)이라 함

A에 $\vdots$ 를 사용해 $\mathrm{b}$ 를 붙여 만든 행렬을 첨가행렬(augmented matrix)이라 함

$n$ 개의 미지수를 갖는 $m$ 개의 일차방정식들을 세 개의 행렬로 나타낼 수 있다는 것을 알자!

2.2 Gauss 소거법과 Gauss-Jordan 소거법

선형연립방정식을 풀 때 사용하는 소거법을 체계화하는 것이 목표
선형연립방정식은 소거법을 이용하여 풀이
- 모든 방정식을 만족하는 $x,\ y$ 값을 찾는 과정 즉, 방정식에서 변수의 개수를 줄여 정확한 값을 찾는 것
기본행 연산(ERO, Elementary Row Operations): 소거법에서 행한 연산의 종류
- 두 식을 교환(방정식 사이의 순서가 바뀌어도 상관 없음)
- 한 식에 0이 아닌 실수를 곱함
- 한 식에 0이 아닌 실수배를 하여 다른 식에 더함
  » 일반적인 방정식 풀이 방법이라고 생각하면 된다. 후에 행렬에 대한 기본행 연산으로 확장

정의 [행 사다리꼴(REF)과 기약 행 사다리꼴(RREF)]

$m \times n$ 행렬 $E$ 가 아래 세 가지를 만족할 때 행 사다리꼴(row echelon form, REF)

성분이 모두 0인 행이 있다면 그 행은 행렬의 맨 아래에 위치

각 행의 첫 번째 0이 아닌 성분은 1, 이것을 그 행의 선행성분(leading entry, leading 1)이라 함

$i$ 행, $(i+1)$ 행 모두에 선행성분이 존재하면 $(i+1)$ 행의 선행성분은 $i$ 행의 선행성분보다 오른쪽에 위치

여기에 추가적으로 다음 성질을 만족하면 기약 행 사다리 꼴(reduced row echelon form, RREF)

선행성분(leading entry in row)을 포함하는 열의 선행성분 외의 성분은 모두 0

REF 행렬 예시
$\begin{bmatrix} 1 & 4 & 2 & 3 & -6 \\ 0 & 0 & 1 & 0 & 3 \\ 0 & 0 & 0 & 1 & 8 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}$
RREF 행렬 예시 (4번째 성질만 추가)
$\begin{bmatrix} 1 & 4 & 0 & 0 & -6 \\ 0 & 0 & 1 & 0 & 3 \\ 0 & 0 & 0 & 1 & 8 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix}$

정의 [기본행 연산(ERO)]

위에서 선형연립방정식에 대해 설명한 것을 행렬로 확장하여 이해하기

$m \times n$ 행렬 $A$ 에 관한 다음 연산을 기본행 연산(elementary row operation, ERO)이라 함

$A$ 의 두 행 $i$ 행과 $j$ 행을 서로 바꿈 $R_i \leftrightarrow R_j$

$A$ 의 $i$ 행에 0이 아닌 상수 $k$ 를 곱함 $kR_i$

$A$ 의 $i$ 행을 $k$ 배하여 $j$ 행에 더함 $kR_i + R_j$

기본행 연산의 핵심은 주어진 행렬을 REF, RREF로 바꾸는 것

행렬 $A$ 에 기본행 연산을 시행해 얻는 행렬을 $B$ 라고 하면 $A,\ B$ 는 행동치(row equivalent)

만약 두 선형연립방정식의 첨가행렬( $A,\ \mathrm{b}$ 행렬의 결합)이 행동치라면 이들은 동치이다. 즉, 해집합이 같다는 의미이다. 이는 Gauss 소거법의 핵심으로, 선형연립방정식의 해를 구하는 데에 사용

행렬의 REF와 RREF 구하기

1 단계

성분에 0이 아닌 수가 존재하는(모두는 0이 아닌) 가장 좌측열 찾음

2 단계

1 단계에서 찾은 열의 가장 위 성분이 0이라면 그 열의 위에서부터 처음으로 0이 아닌 성분을 포함하는 행과 1행을 교환
- 가능하다면 교환하는 성분이 1, -1, 2이면 좋음

3단계

1행의 선행성분을 1로 만들기 위해 1행의 모든 성분을 첫째 성분으로 나눔

4단계

1행의 선행성분 아래의 모든 성분을 0으로 만듦
- 1행을 $k$ 배 하여 더하는 등 기본행 연산으로 가능

5단계

1행을 제외한 나머지 부분에 대해 1 단계부터 4 단계를 반복

RREF로 만들고 싶다면

선행성분이 존재하는 열에 대해, 선행성분을 포함한 행에 $k$ 배를 한 후 그 외 행에 연산하여 성분을 0으로 만드는 것이 가능

응용방법

주어진 선형 방정식을 방정식 관점의 소거법으로 푸는 것이 아니라, Gauss 소거법(REF로 만드는 소거법)을 이용해 풀 수 있음
선형연립방정식 » 첨가행렬로 표현 » 기본행연산을 통해 REF 구함 » 이를 첨가행렬로 갖는 선형연립방정식을 표현(기존의 선형연립방정식보다 훨씬 간단한 모양) » 해를 구하기 쉬움

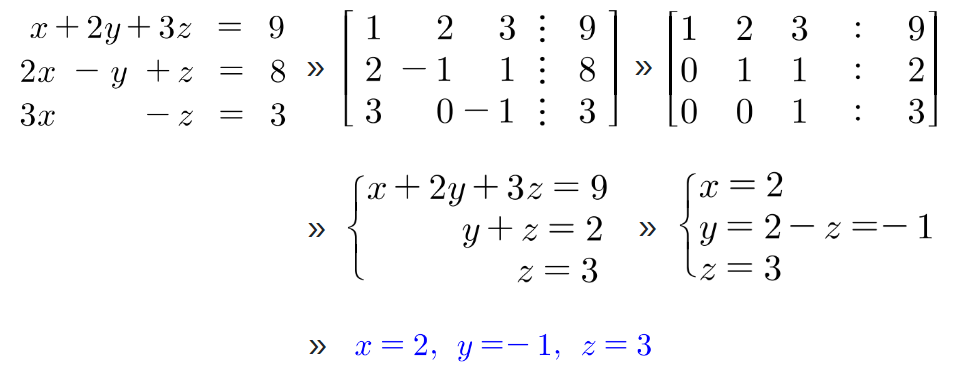
물론 Gauss-Jordan 소거법(RREF로 만드는 소거법)을 이용하면, 선형연립방정식의 마무리 연산을 행렬 관점의 소거법으로 해결하므로 거의 바로 해를 구하는 것이 가능
Gauss 소거법 $A \xrightarrow{\text{ERO}} \mathrm{REF}(A)$
Gauss-Jordan 소거법 $A \xrightarrow{\text{ERO}} \mathrm{REF}(A) \xrightarrow{\text{ERO}} \mathrm{RREF}(A)$
자유변수와 선행변수
- 자유변수: 첨가행렬의 RREF 중 선행성분 1을 포함하지 않는 열에 대응하는 변수
- 선행변수: 선행성분 1을 포함하는 열에 대응하는 변수
  » RREF에서 결국 선형연립방정식으로 바꾸어 변수에 해당하는 값을 알아야 하는데 이때 각 열은 특정 변수를 나타내고, 그것이 자유변수와 선행변수로 나뉜다고 이해

동차(homogeneous)연립방정식

a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = 0

a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = 0

\vdots

a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = 0

위 식은 앞서 제시한 선형연립방정식에서 우변 $b$ 가 0인 동차연립방정식으로 $\mathrm{x} = 0$ 을 자명한 해(trivial solution)로 가짐
동차연립방정식은 유일한 자명한 해를 갖는 경우, 무수히 많은 해를 갖는 경우 두 가지만 존재
무수히 많은 해를 갖는 경우는 자유변수를 임의의 실수로 설정하는 경우

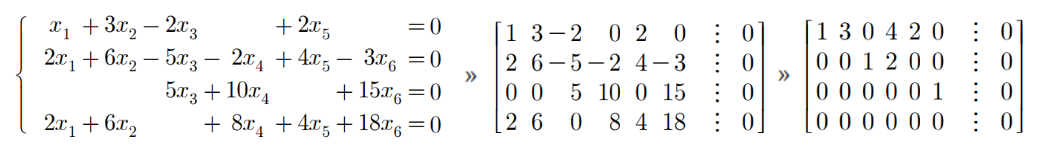
위 문제의 경우 변수가 6개, 방정식이 4개
다만 RREF로 표현하면 0으로만 이루어진 맨 밑 행이 제거되는 셈
3개의 선행변수 $x_1,\ x_3,\ x_6$ 와 3개의 자유변수 $x_2,\ x_4,\ x_5$
- 자유변수 3개에 실수 $r,\ s,\ t$ 를 지정하고, 선행변수 3개를 이것으로 표현
- (참고) 이 해법은 동차든 아니든 상관없이 적용
$n$ 개 미지수를 갖는 동차연립방정식에 대해 첨가행렬의 RREF가 $k$ 개의 선행성분 1을 가지면 해집합은 $n-k$ 개의 자유변수를 가짐
- 자유변수가 있냐 없냐로 나뉘니까 자명한 해를 갖든, 무수히 많은 해를 갖든 둘 중 하나인 것!
- $m < n$ 이면, 동차선형연립방정식은 항상 자명하지 않는 해를 가짐 즉, 적어도 하나의 자유변수를 가진다는 것.