네이버 부스트캠프 AI Tech 4기 선형대수학 스터디 5회차
선형대수학 이상구 저 Chapter6
6.3 핵과 치역
정의
- 이 선형변환이면, 에 의한 상이 이 되는 안의 벡터 전체의 집합을 의 핵(kernel)이라 하고 로 나타냄. 즉
- 다시 말해, 안의 어떤 벡터 를 로 선형변환 했을 때 옮겨진 공간에서 이 되는 벡터들을 이 변환 의 핵이라고 한다는 것이다.
- 변형의 결과를 0으로 만드는 조건이 이 변형의 핵이라는 것!
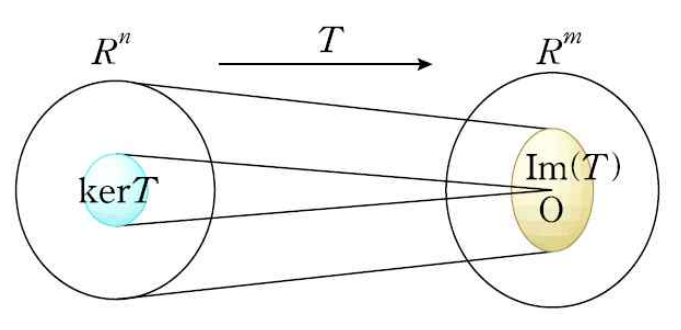
- 이 그림은 을 이야기할 때도 등장한다.
- (예제 1) 인 선형변환 에 대해 를 구한다면, 을 만족해야 하므로
- (예제 2) 인 선형변환 에 대해 를 구한다면, 이므로 따라서
- 두 예제에서 를 표현하는 방식도 알아두자
정의
- 변환 가 를 만족하면 단사(one-to-one, injective)
- 어떤 벡터와 선형변환된 상이 일대일대응한다는 뜻
- 변형된 결과가 같다? 두 벡터는 같은 벡터다!
- 단사일 필요충분조건은
- 변환 가 임의의 에 대해 인 이 존재하면 전사(onto, surjective)
- 변환된 공간에서의 어떤 벡터에 해당하는 원상이 변환 이전 공간에 존재한다면 전사
- 둘은 양립할 수 있는 개념
- 어떠한 선형변환이 단사임을 확인하려면?
- 이어야 단사
- 왜? 변형이 선형성을 가지는 선형변환이므로... 증명 참조
- 즉, 에서 선형변환한 상 를 만족하는 가 이면 됨
- (예제 3) 라면, 을 만족하는 것은 이 유일함. 따라서 이므로 단사
- 이어야 단사
선형변환 식을 0으로 만드는() 변수()들의 값이 모두 0으로 유일하다면 단사!
- 에서 는 의 부분공간이므로 를 핵공간(kernel)이라 부름
- 안에서 에 의한 상이 이 되는 벡터들의 집합이므로 공간도 형성할 수 있는 것
- 공간은 어떤 집합에 속하는 벡터들의 일차결합으로 형성되는 것을 의미하였음
- (예제 5) 우리는 행렬도 선형변환이라고 배웠다. 그러니까 행렬은 변환의 일종이고, 당연히 도 구할 수 있다! 방법은 위에서 배운 것을 사용하면 되겠지?
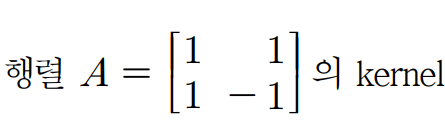
- 위의 행렬 는 행렬이므로 벡터 를 선형변환한다.
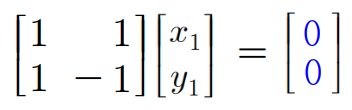
- 따라서 를 구하기 위해서는 위와 같이 (변형의 결과가 0)이어야 한다.
- 이는 연립방정식 과 을 푸는 것과 같다. 여기서 은 모두 0으로 유일하므로 해당 행렬은 이고, 단사라고 할 수 있다.
정의 [동형사상]
- 변환 에 대해, 임의의 의 상 전체의 집합을 의 치역(range)이라 하고 로 나타냄.
- 특히 이면(공역과 치역이 같다는 의미) 는 전사(surjective, onto).
- 으로부터 변환된 상이 전체를 커버하기 때문에 공간의 모든 벡터의 원상이 에 존재할 수밖에 없음. 이는 앞서 이야기한 전사의 조건에 부합.
- 선형변환 가 단사이고 전사( 전단사)이면 이 되고, 를 에서 으로의 동형사상(isomorphism)이라고 함.

- (예제 6) 의 치역?
- 는 아무런 제약 조건이 없으므로 실수 전체를 치역으로 가짐. 따라서 임의의 실수 로 표현
- 이는 의 모든 부분을 커버하지 못하므로(공역 치역) 전사가 아님
- 따라서 전단사가 아니므로 동형사상이 될 수 없음
- (예제 7) 아래 선형변환에 대해 알아보자.
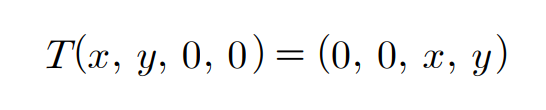
- 이므로 단사
- 이 되는 가 모두 0이 유일
- 이므로 전사
- 집합 , (공역)이고, 변환하여도 에 특별한 조건이 없으므로 치역이 가 되고 이는 공역인 공간을 모두 커버 가능
- 따라서 전단사이고, 동형사상
- 는 의 부분공간
다시 정리해보자.
- 단사 조건:
- 전사 조건: (은 선형변환된 공간)
- 단사, 전사 모두 만족하면 전단사이고, 이 변환 는 동형사상
- 는 의 부분공간
- 는 의 부분공간
- 행렬 에 대한 선형변환 에 대해 아래 두 성질 만족
- 가 단사 의 열벡터들이 일차독립
- 가 전사 의 행벡터들이 일차독립
- 이들의 증명 역시 위 단사 및 전사 조건에 입각하여 유도


- 행렬 가 차 정사각행렬, 가 선형연산자이면, 가 단사일 필요충분조건은 가 전사라는 것
- 선형연산자가 뭐였지? 에서 자신으로 선형변환 (Chapter6. 선형변환 참고)

- 선형연산자가 뭐였지? 에서 자신으로 선형변환 (Chapter6. 선형변환 참고)
- 그렇다면, '열벡터가 일차독립', '행벡터가 일차독립' 등은 가역행렬의 동치정리에 속한 조건이므로 단사와 전사도 가역행렬의 동치 정리에 추가할 수 있음
- 가역행렬의 동치정리

6.4 선형변환의 합성과 가역성
- 합성변환은 두 개 이상의 선형변환이 연속적으로 수행
- 와 이 모두 선형변환이면 합성함수 도 선형변환
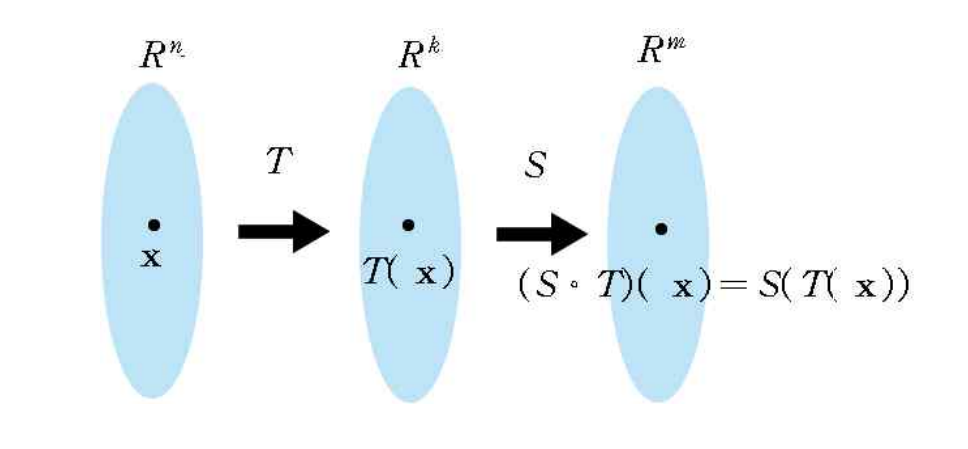
- 와 이 모두 선형변환이면
- 가 단사이면, 가 단사
- 가 전사이면, 가 전사
- 이처럼 선형변환이 합성된 경우에 이에 대응하는 표준행렬은 합성된 변환 각각의 표준행렬의 곱으로 표시
- (예제 2) 아래와 같이 원을 변환시키는 행렬변환?
- 은 를 3배, 를 2배 하는 변환
- 는 회전하는 변환
- 합성할 때 나중에 적용하는 것이 감싸는 형태이고, 그에 따라 행렬 연산 순서 정함
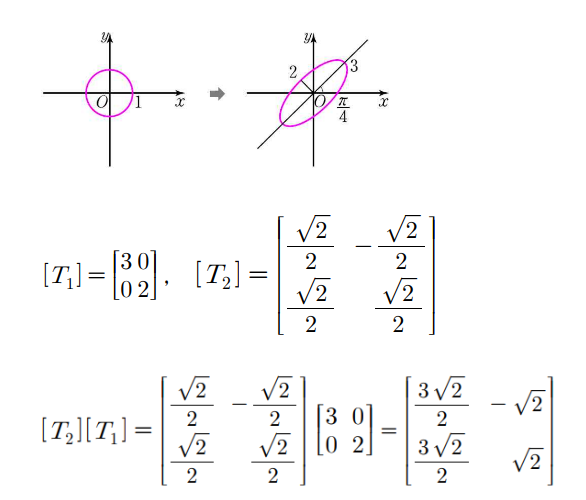
- 세 개 이상의 선형변환 합성함수에 대해서도 표준행렬의 연산순서에 따른 곱으로 나타냄
- 함수 가 가역일 필요충분조건은 가 전사이면서 단사(전단사)
- 선형변환 이 가역이면 도 선형변환
