BoostCamp AI Tech 4기 논문 스터디 6회차

Neural Graph Collaborative Filtering

---

Abstract

• 유저와 아이템에 대한 Learning vector representations(학습 벡터 표현, Embedding)은 현대 추천 시스템의 핵심
  • 초기 Matrix Factorization(MF)부터 현재의 딥러닝까지, 유저 혹은 아이템의 속성(ID 등)을 mapping하여 Embedding을 얻음
• 하지만 기존의 Embedding은 유저와 아이템의 상호작용(Collaborative signal)을 나타내지 못한다는 결점이 존재
  • 유저와 아이템별로, 각 feature별로 mapping하다보니 관계를 나타내기 어렵다는 것
  • 이로써 이것은 collaborative filtering 효과를 얻기에 충분하지 않을 수도
• bipratite graph structure로 나타나는 유저-아이템 상호작용을 Embedding에 사용할 것을 주장
• 새로운 추천 framework인 Neural Graph Collaborative Filtering(NGCF)
  • 유저-아이템 graph에 Embedding을 전파하는(propagationg) 방식을 사용
  • Embedding 과정에 explicit 방식으로 collaborative signal을 주입
  • 이것은 유저-아이템 그래프의 high-order connectivity를 표현하는 모델로 이어짐
  • 3가지 벤치마크에 대한 실험을 수행해 여러 최신 모델에 비해 개선된 성능을 보여줄 것

KEYWORDS

• Collaborative Filtering
• Recommendation
• High-order Connectivity
• Embedding Propagation
• Graph Neural Network

유저-아이템의 관계를 나타내는 graph에 어떤 방식으로 Embedding을 전파한다는 것일까? 결국 어떻게 상호작용을 포함한 Embedding이 가능한 것일까?

1. INTRODUCTION

• 개인화된 추천의 핵심은 과거의 상호작용 기반으로 유저가 어떤 아이템을 선택할 가능성을 추정하는 것
• 여기서 CF는 행동적으로 유사한 유저가 같은 아이템에 대해 비슷한 선호를 보인다고 가정
  • 과거의 상호작용을 재구성하기 위해 유저와 아이템을 매개변수화하여, 그 매개변수를 기반으로 선호도를 예측
• 학습 가능한 CF 모델의 주요 구성 요소는 아래 두 가지
  • Embedding: 유저와 아이템을 벡터로 표현
  • Interaction modeling: Embedding 기반으로 과거의 상호작용을 재구성
    • MF의 경우 유저와 아이템의 ID를 Embedding하고, 상호작용을 내적으로 나타냄
    • NCF의 경우 MF의 상호작용 함수(내적)를 비선형적 신경망으로 대체하여 사용
    • translation-based CF의 경우 상호작용 함수로 Euclidean distance metric 사용
  • 이렇듯 상호작용을 재구성하는 방식을 다르게 할 수 있음
• 다만 위 방식은 여전히 CF에 대해 만족스러운 Embedding을 생성한다고 볼 수 없음
  • 이들은 기술적인(descriptive) feature만을 가지고 Embedding 함수를 만들지, 유저와 아이템의 상호작용을 고려하고 만드는 것이 아니기 때문
  • 이들에게 상호작용은 학습을 위한 목적함수를 정의할 때만 사용되는 것
  • 결과적으로 Embedding이 CF에 적합하지 않으면, 차선책으로 상호작용 함수에 의존하게 되는 것(위 예시 방식들처럼)

기존의 방식들은 유저-아이템 상호작용을 고려하지 않고 Embedding + 따로 상호작용 함수에 의존하여 학습하는데, 이것이 CF에 적합하지 않다는 주장
Embedding을 할 때부터 상호작용을 고려해야 하지 않을까? 그럼 어떻게?

• 유저-아이템 상호작용을 Embedding에 잘 통합하는 것은 쉽지 않음
• 실제로 상호작용은 굉장히 많을텐데, 어떻게 원하는 collaborative signal을 만들 수 있을까?
  • collaborative signal은 상호작용을 나타내는 신호라고 생각하자
• 유저-아이템 상호작용에서 high-order connectivity을 사용하자! 그것이 interaction graph structure에서 collaborative signal을 인코딩하는 자연스러운 방법!

Running Example

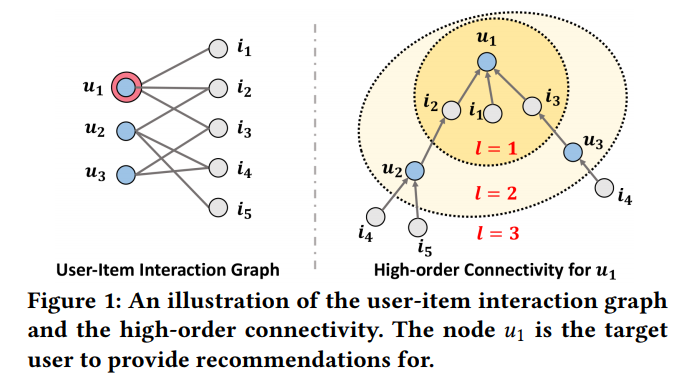
• Figure 1은 high-order connectivity를 그림으로 나타낸 것
• $u_1$ 기준으로 유저-아아템 상호작용과 high-order connectivity를 볼 수 있음
• 모든 유저, 아이템 node로부터 1이상인 길이 $l$을 지나 $u_1$으로 도달
• 길이 $l$에는 high-order connectivity를 표현하는 풍부한 의미가 담겨 있음
  • $l$을 통해 연결된 두 유저는 서로 유사
  • 유저와 $l$을 통해 연결된 아이템을 소비할 가능성이 있음
  • $l$이 작을수록, 경로가 많을수록 더 관계있다고 볼 수 있음

Present Work

• Embedding 함수에 high-order connectivity 정보를 모델링할 것을 제안
• 다만 구현이 복잡한 트리 구조를 확장하지 말고, 그래프에 재귀적으로 Embedding을 전파하는 신경망 방식을 설계
• embedding propagation layer
  • 서로 관계된 아이템의 Embedding을 유저의 Embedding에 통합하는 방식으로 유저 Embedding을 개선(혹은 유저의 Embedding을 아이템 Embedding에 통합하는 반대 과정)
  • 이 layer를 다중으로 쌓으면 high-order connectivity에서 collaborative signal을 포착하는 게 가능
  • 즉 $n$개의 layer를 쌓는다면 $l = n$인 관계까지 포착하는 게 가능한 것
  • 이러한 NGCF의 타당성과 효율성을 증명하기 위해 실험할 것
• 기존의 HOP-REC은 train data의 풍부함을 위해서만 high-order connectivity를 사용하고, prediction model에선 MF가 유지
• 이와 달리 NGCF는 high-order connectivity을 prediction model에도 사용, 경험적으로 CF에 더 적합한 Embedding을 산출한다는 것을 보여줄 것

2. METHODOLOGY

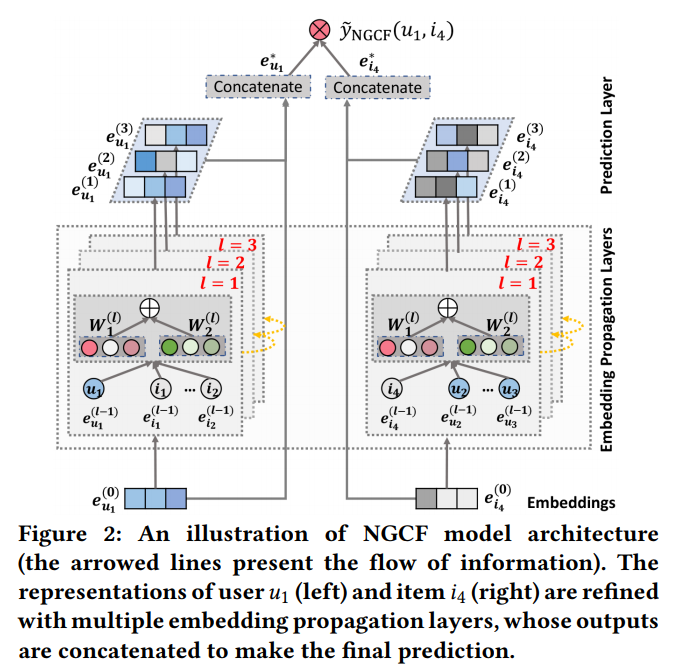
• Figure 2의 모델 구조
  (1) Embedding layer
  유저와 아이템 Embedding 제공 및 시작
  (2) multiple embedding propagation layers
  high- order connectivity relations 주입해 Embedding 개선
  (3) prediction layer
  서로 다른 propagation layers의 Embedding 통합, 유저-아이템 쌍의 친밀감(affinity) 점수 출력

2.1 Embedding Layer

• 유저 $u$는 Embedding vector $\mathrm{e}_u \in \mathbb{R}^d$로 Embedding
• 아이템 $i$는 Embedding vector $\mathrm{e}_i \in \mathbb{R}^d$로 Embedding
• 이는 Embedding look-up table로 이어짐
  $\mathrm{E} = [ \mathrm{e}_{u_1},\ \cdots,\ \mathrm{e}_{u_N}\ \ ,\ \ \mathrm{e}_{i_1},\ \cdots,\ \mathrm{e}_{i_M}]$
• 이는 end-to-end 방식으로 최적화될 유저 및 아이템 Embedding의 초기 상태로 사용
• NGCF에서는 이 Embedding을 유저-아이템 상호작용 그래프에 전파하여 개선시킴
  • collaborative signal을 명시적으로 주입하여 효과적인 Embedding이 되도록 만드는 단계

2.2 Embedding Propagation Layers

• 그래프 구조를 따라 CF signal을 파악하고, 유저 및 아이템 Embedding을 개선하기 위해 GNNs의 message-passing 구조를 차용

2.2.1 First-order Propagation

one-layer propagation을 먼저 살펴보기

• 관계를 가지는 아이템은 유저의 선호도에 대한 직접적인 증거를 제시
• 유사하게, 아이템을 소비하는 유저는 아이템에 대한 feature로 다루어짐
  • 두 아이템의 유사성을 반판하는 수단이기도 함
• 결국 연결된 유저와 아이템 Embedding 전파를 위해 두 가지 과정을 공식화

Message Construction

• 연결된 유저-아이템 쌍 $(u,\ i)$에 대해, $i$로부터 $u$에게 전달하는 message를 정의
  $\mathrm{m}_{u \leftarrow i} = f(\mathrm{e}_i,\ \mathrm{e}_u,\ p_{ui})$
  $f(\cdot)$ : message encoding function
  $p_{ui}$ : edge $(u,\ i)$를 따라 전파될 때의 decay factor를 조정하기 위한 계수

• 이는 message Embedding 즉, 전파되는 정보를 Embedding하는 식
• $f(\cdot)$는 아래와 같이 정의
  
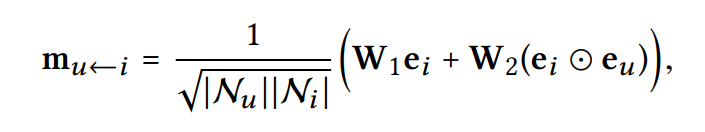
  $\mathrm{W}_1, \mathrm{W}_2 \in \mathbb{R}^{d' \times d}$ : 유용한 정보가 담긴, 학습 가능한 weight matrices
  $d'$ : transformation size
  ${1 \over \sqrt{|\mathcal{N}_u||\mathcal{N}_i|}}$ : GCN에서 $p_{ui}$를 표현하는 식, 여기서 $\mathcal{N}$은 first-hop neighbors
  $\mathrm{e}_i \odot \mathrm{e}_u$ : 관계를 encode하는 element-wise product 식(기존 GCN과의 차별점)
  • 이 식은 message가 $\mathrm{e}_i,\ \mathrm{e}_u$ 사이 친밀감(affinity)dp 의존하는 식이란 것을 의미
• 많은 message를 전달할수록 표현 능력이 증가할 뿐 아니라 추천 성능도 상승
• $p_{ui}$는 과거의 아이템이 유저의 선호에 얼마나 영향을 미치는지를 나타냄

Message Aggregation

• $u$의 이웃으로부터 전파된 message를 통합하여 $u$의 표현력을 개선
• Aggregation 함수는 아래와 같음
  
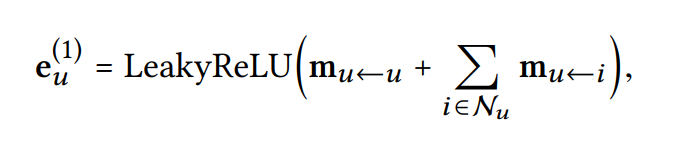
  $\mathrm{e}^{(1)}_u$ : first embedding propagation layer 이후에 유저 $u$가 얻은 표현력을 의미
  $\mathrm{LeakyReLU}$ : 활성함수로, positive, small negative 상호작용 신호를 인코딩
  $\mathrm{m}_{u \leftarrow u}$ : $u$의 원래 feature의 정보를 유지하기 위해 self-connection, 이는 $\mathrm{W}_1\mathrm{e}_u$와 같다고 생각
• 비슷한 방식으로 아이템에 대한 Embedding $\mathrm{e}^{(1)}_i$를 얻음

요약하면, embedding propagation layer의 장점은 first-order connectivity 정보(message)를 사용해 유저와 아이템 표현을 연관시킬 수 있다는 것

2.2.2 High-order Propagation

one-layer propagation을 알았으니, 고차원을 살펴보기

• first-order connectivity modeling에서 embedding propagation layer을 더 쌓아서 표현
• high-order connectivities는 유저와 아이템 사이의 연관 점수를 추정하기 위해 collaborative signal을 인코딩
• $l$개의 embedding propagation layers을 쌓으면 유저와 아이템은 각각 $l$-hop neightbors의 message를 받게 됨
• High-order Propagation 식은 위 First-order Propagation을 변형하여 아래와 같음
  
  
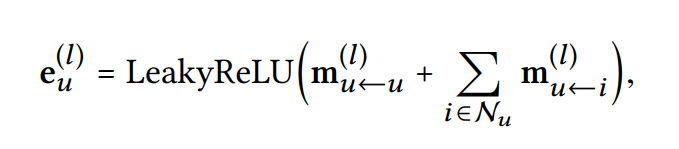
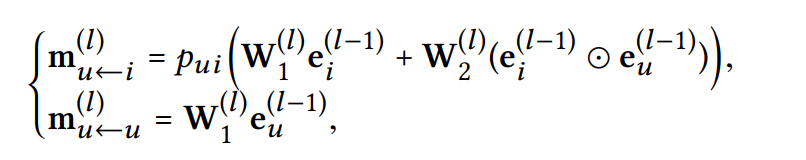
  $\mathrm{W}_1^{(l)},\ \mathrm{W}_2^{(l)} \in \mathbb{R}^{d_l \times d_{l-1}}$ : 학습 가능한 weight matrices
  $d_l$ : transformation size
  $\mathrm{e}_i^{(l-1)}$ : 이전 message-passing 단계에서 온 representation, ($l - 1$)-hop neighbors의 message를 기억하여 $l$ layer에서 아이템 $i$의 표현을 얻을 수 있음

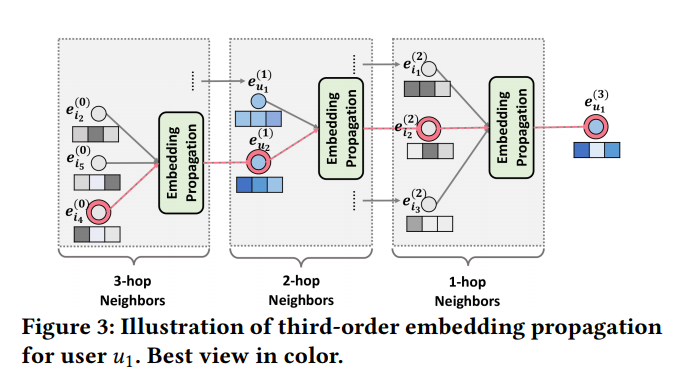
• Figure 3에서처럼 $i_4$에서 $u_1$에게 오는 message를 받는다면 3-hop neighbor로부터 온 것이므로 $\mathrm{e}_{u_1}^{(3)}$

이처럼 multiple embedding propagation layers를 쌓은 것은 collaborative signal을 representation(표현)에 균일하게 주입하는 것

Propagation Rule in Matrix Form

• embedding propagation의 전체적인 관점과 일괄 적용을 위해 matrix form의 layer-wise propagation rule을 제시

위에서는 계속 각각의 유저, 각각의 아이템에 대한 message 수신이었지만 이제는 하나의 layer로 확장하여 matrix 관점에서 보자

• 그 식은 아래에 제시
  
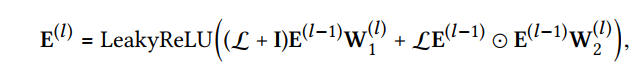
  $\mathrm{E}^{(l)} \in \mathbb{R}^{(N + M) \times d_l}$ : $l$ 단계의 embedding propagation 이후 얻는 유저와 아이템 표현
  $\mathrm{E}^{(0)}$이라면 첫 message-passing을 의미
  $I$ : identity matrix
  $\mathcal{L}$ : 유저-아이템 그래프의 Laplacian matrix
  
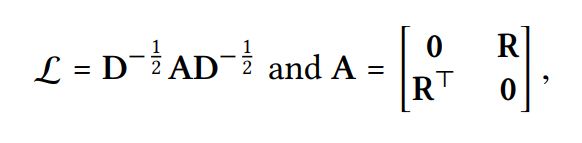
  $\mathrm{R} \in \mathbb{R}^{N \times M}$ : 유저-아이템 상호작용 matrix
  $0$ : 모두 0인 matrix
  $A$ : adjacency matrix
  $D$ : diagonal degree matrix, t-th diagonal element $D_{tt}$는 $|\mathcal{N}_t|$ ($\mathcal{N}$은 first-hop neighbor였음)
• matrix-form propagation rule을 통해 모든 아이템과 유저에 대한 표현을 동시에 업데이트가 가능
  • 이는 node sampling procedure을 하지 않아도 됨
  • large-scale graph에 대한 GCN에서 작동하게 함(복잡성에 대한 분석은 2.5.2에서)

2.3 Model Prediction

• $L$ Layer 전파 이후, 유저 $u$에 대한 복수의 표현을 가지게 됨
  $\{\mathrm{e}_u^{(1)},\ \cdots \ \mathrm{e}_u^{(L)}\}$
  • 이들은 각자 다른 층으로부터, 다른 message를 전달해 만들어졌으므로 유저 $u$의 선호도를 표현하는데 각기 다른 기여도를 가질 것임
  • 따라서 유저에 대한 마지막 Embedding을 통해 concatenate 해야 함
  • 물론 아이템에 대해서도 동일한 작업을 해야 함
• concatenate 방식은 아래와 같음
  • 여기서 concatenate를 할 때 $p_{ui}$를 사용하여 가중치를 설정하는 것
  • 아래 식에서는 가중치가 고려된 점을 알 수 없이 그냥 concatenate 하는 것으로 이해됨

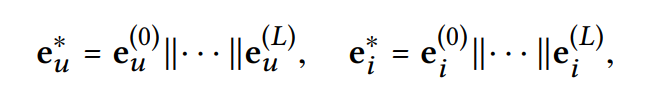
$||$ : concatenation operation

• initial embeddings를 풍족하게 할 뿐만 아니라 $L$을 조정해 전파의 범위를 조절하는 것이 가능
• 추가적인 학습 parameter가 필요 없고, layer-aggregation mechanism을 사용하는 GNN에서 꽤 효율적
• 최종적으로 목표 아이템에 대한 유저의 선호를 추정하기 위해 inner product를 거침
  
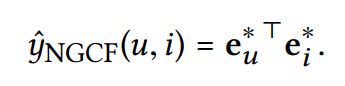
• embedding function learning의 중요성을 강조하기 위해 간단한 innner product 상호작용 함수를 사용할 것
  • 추가적인 복잡한 선택은 future work

유저와 아이템의 상호작용이 포함된 message를 반영하여 다양한 Embedding을 만들고, 이들을 concatenate 하여 결국 상호작용이 반영된 Embedding을 하게 되었음. 어찌됐든 상호작용을 반영한 Embedding이 중요하다는 걸 보여주기 위함이니 최종 Embedding 과정에서 간단한 inner product를 사용함.

2.4 Optimization

• parameter 학습을 위해 pairwise BPR loss를 최적화
  • 이는 추천 시스템에서 집중적으로 사용
  • 관측된 것과 관측되지 않은 것 사이의 상대적인 순서를 고려
  • 유저는 관측한 것을 관측하지 않은 것보다 더 선호한다고 가정

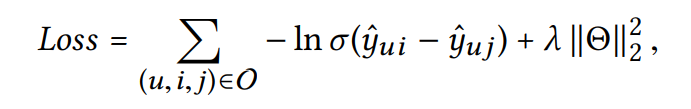
$\mathcal{O} = \{(u,\ i,\ j)|(u,\ i) \in \mathcal{R}^+, (u,\ j) \in \mathcal{R}^-\}$ : pairwise 훈련 데이터
$R^+$ : 관측된 상호작용
$R^-$ : 관측되지 않은 상호작용
$\sigma(\cdot)$ : sigmoid function
$\Theta = \{\mathrm{E}\{\mathrm{W}_1^{(l)},\mathrm{W}_2^{(l)}\}^L_{l=1}\}$ : 학습 가능한 parameter
$\lambda$ : $L_2$ regularization, overfitting 방지

• mini-batch Adam 사용하여 모델 최적화 및 parameter 업데이트
• 무작위로 뽑은 샘플 $(u,\ i,\ j) \in \mathcal{O}$에 대해 앞서 설명한 방식대로 $L$번 전파를 마치면 $[\mathrm{e}^{(0)}, \cdots, \mathrm{e}^{(L)}]$이라는 표현을 얻을 것

2.4.1 Model Size

• NGCF는 각 layer마다 embedding matrix $\mathrm{E}^{(l)}$를 가지고, $d_l \times d_{l-1}$ 사이즈의 두 개 weight matrices(parameter)를 가짐
  • 이 weight matrices는 embedding look-up table $\mathrm{E}^{(0)}$로부터 파생
  • MF와 비교하면 NGCF는 $2Ld_ld_{l-1}$만큼 더 parameter를 가지는 것
  • 하지만 보통 $L$은 5 이하이고, $d_l$은 embedding size로 설정되는데 이는 유저와 아이템의 수보다 적음
  • (예시) 20k 유저와 40k 아이템 데이터에 대해 MF는 4.5 million parameter를 사용하는데, 3 겹의 $64 \times 64$ propagation layer를 사용하면 $2 \times 3 \times 64 \times 64 = 0.24$million개만이 추가될 뿐

2.4.2 Message and Node Dropout

• 딥러닝 모델은 강력한 표현 능력, 하지만 overfitting의 어려움
• Dropout은 overfitting에 대한 효과적인 솔루션
• NGCF에서는 node dropout과 message dropout을 채택
  • message dropout은 보내는 message의 무작위 삭제, 확률 $p_1$
  • 그러면 부분적인 message는 표현을 정제하게 됨
  • node dropout은 무작위로 특정 node를 막고, 거기서 나오는 모든 message를 버림
  • $l$-th propagation layer에서는, Laplacian matrix에서 $p_2$ 확률로 $(M + N)p_2$개의 node를 drop
• dropout은 훈련에서만 사용, 테스트에서는 비활성화
• message dropout은 유저와 아이템 사이의 single connections 표현에 robustness 부여
• node dropout은 특정 유저나 아이템의 영향을 줄임

2.5 Discussion

NGCF에서 SVD++의 일반화 방식, 시간 복잡도 계산

2.5.1 NGCF Generalizes SVD++

• SVD++는 high-order propagation layer가 없는 NGCF의 특별 case
• $L$을 1로 잡는 것과 같음 즉 transformation matrix and nonlinear activation function이 disable
• 결국 얻은 $\mathrm{e}_u^{(1)},\ \mathrm{e}_i^{(1)}$이 최종 $u,\ i$의 표현
• 이걸 NGCF-SVD 모델 공식으로 나타내면
  
  $p_{ui'}$ : $1/\sqrt{\mathcal{N}_u}$
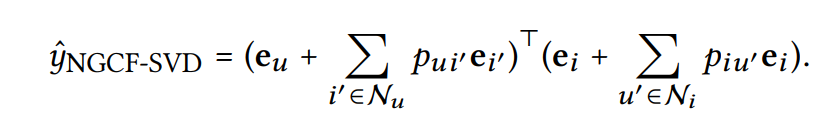
  $p_{u'i}$ : 0
• 정확히 SVD++ 모델을 재현
  • item-based CF model, FISM도 NGCF의 특별 case로 볼 수 있음

2.5.2 Time Complexity Analysis

• layer-wise propagation rule이 주요 작업
• $l$번 layer에서 matrix multiplication을 하는 것에 대한 복잡도는 $O(|\mathcal{R}^+|d_ld_{l-1})$
  • $|\mathcal{R}^+|$ : Laplacian matrix의 0이 아닌 것들
  • $d_l,\ d_{l-1}$ : 현재의, 이전의 transformation size
• prediction layer에서는 한 번의 inner product로, 시간 복잡도는 $O(\Sigma^L_{l=1} |\mathcal{R}^+|d_l)$
• 전체적인 시간복잡도는 위의 것을 합한 것
  • 동일한 dataset에 대해 train 시 한 epoch당 MF는 20s, NGCF는 80s 소요
  • inference 시 MF는 80s, NGCF는 80s 소요

3. RELATED WORK

• NGCF와 아래의 모델 사이의 비교
  • Model-Based CF Methods
  • Graph-Based CF Methods
  • Graph Neural Network-Based Methods

3.1 Model-Based CF Methods

• 최신 추천 시스템은 유저와 아이템을 벡터화, 유저-아이템 상호작용 데이터를 재구성

3.2 Graph-Based CF Methods

3.3 Graph Convolutional Networks

4. EXPERIMENTS

4.1 Dataset Description

4.2 Experimental Settings

4.3 Performance Comparison (RQ1)

4.4 Study of NGCF (RQ2)

4.5 Effect of High-order Connectivity (RQ3)

5. CONCLUSION AND FUTURE WORK