단순 선형 회귀를 통한 회귀 이해

단순 선형 회귀는 독립변수와 종속변수가 모두 1개인 선형 회귀다. 예를 들어 집이 넓으면 주택 가격도 높아지는 경향이 있고, 이를 하나의 그래프로 그리면 아래와 같다.

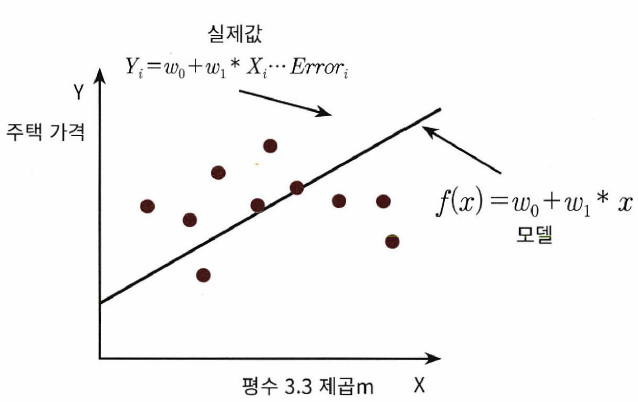
위 그래프에서 볼 수 있듯 현실 데이터는 우리가 그린 회귀선에 딱 맞는 법이라곤 없다. 따라서 언제나 오류값(error)이 존재할 수밖에 없고, 우리는 현실을 잘 반영하는 회귀선을 판단할 때 이 오류값이 얼마나 작은가를 놓고 본다. 아래는 오류값에 대한 그래프이다.

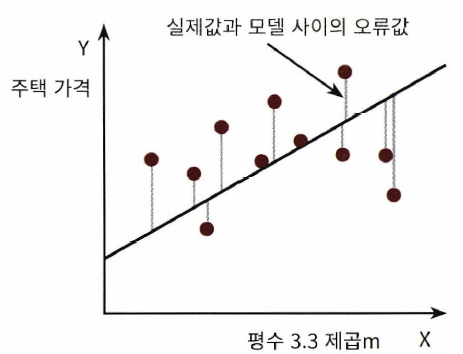
오류값은 회귀선에서 실제 데이터 사이의 크기이다. 그런데 회귀선 위아래로 현실 데이터가 분포해 있으므로 오류값들을 그냥 더하게 되면 0이 되버린다. 따라서 오류값에 제곱을 하거나(RSS, Residual Sum of Square) 절대값을 씌운다.(Mean Absolute Error) 보통 미분 등 계산을 편리하게 하기 위해 RSS를 많이 사용한다. 다음은 RSS를 수식으로 표현한 것이다.

$RSS(w_0, w_1) = \frac{1}{N} \Sigma_{i=1}^N(y_i - (w_0 + w_1 \times x_i))^2$

위 식은 $w_0$과 $w_1$을 업데이트 하는데, 예측값(=$w_0 + w_1 \times x_1$)을 실제값(=$y_i$)에서 뺀 것을 제곱을 해준다고 해석한다. $w_0$은 절편(bias)이고 $w_1$는 독립변수 $x_1$의 회귀 계수이다. 데이터 건수는 $i$부터 $N$까지 있다.

중요한 점은 회귀식이 다른 수학에서처럼 $y$나 $x$가 중심이 되는 것이 아니라 $W$가 중심이 된다는 것이다.