규제 선형 모델 - 릿지, 라쏘, 엘라스틱넷

앞서 살펴봤던 변수가 15개인 회귀처럼 과대적합한 모델은 다항식이 복잡해지고 회귀계수가 크게 설정되어 성능이 많이 떨어졌다. 따라서 회귀의 중점은 손실값도 작으면서 회귀계수가 너무 크지 않게 해야한다.

지금까지는 $W$를 업데이트 하는 기준은 오차값을 최소화하는 방향으로만 설정했다면, 이제는 절절한 모델을 만들기 위해 $W$가 너무 커지지 않게 하는 기준도 필요하고, 릿지와 라쏘 등 규제 모델이 만들어지게 되었다.

규제의 수식은 아래와 같다.($W$의 크기를 제한하기 위한 새로운 항이 추가된 것을 확인해보자)

$Cost = RSS(W) + \alpha \parallel W\parallel_2^2$

$\alpha$는 학습 데이터에 적합하는 정도와 회귀계수의 크기를 제어하는 키 포인트이다. $\alpha$는 어떤 역할을 할까?

• $\alpha$가 0 혹은 매우 작은 수일 때
  • $\alpha \parallel W \parallel_2^2$의 크기가 0이되므로 $Cost = RSS(W)$ 자체가 된다.
  • 따라서 이 때에는 $W$에 대한 규제가 없으므로 $W$가 어느 정도 커져도 $Cost$를 크게 증가시키지 않기 때문에 상쇄가 가능하다.
• $\alpha$가 $\infin$ 혹은 매우 큰 수일 때
  • $Cost$가 너무 커지게 되므로 $W$를 줄여 $\alpha \parallel W \parallel_2^2$ 항의 크기를 줄이기 위해 $W$를 작게 만든다.

릿지 회귀

릿지 회귀는 모든 feature에 대해 $W$의 값을 줄이긴 하되 0으로 만들지는 않는 규제 방법이다. 릿지 회귀 L2 규제라고도 하며 sklearn.linear_model안에 Ridge 클래스로 구현이 되어있다.

from sklearn.linear_model import Ridge

model = Ridge(alpha=10)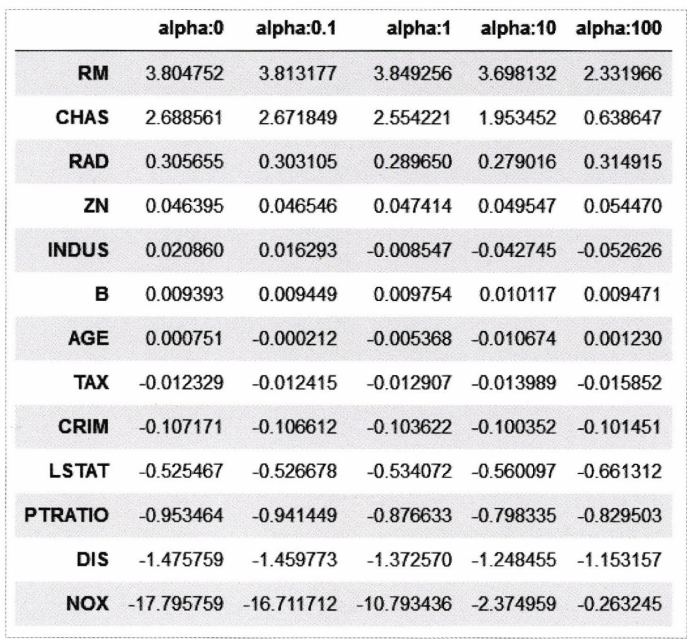

위 사진은 릿지 모델의 결과이다. $\alpha$의 크기를 변경해가며 각 변수마다 회귀 계수를 나타낸 것이다. NOX 변수를 보면, $\alpha=1$에서 $\alpha=10$으로 변경하니 회귀 계수가 크게 줄어든 것을 볼 수 있다. 릿지 모델은 이처럼 몇 개의 회귀 계수만 너무 큰 경우에 사용하면 좋다.

라쏘 회귀

라쏘 회귀는 모든 feature에 대해 $W$의 값을 0으로 만들어 아예 학습에서 제외하여 적절한 feature만 포함시키는 방법이다. 라쏘 규제는 L1 규제라고도 하며 릿지 모델과 마찬가지로 sklearn.linear_model에 Lasso 클래스가 구현되어있다.

from sklearn.linear_model import Lasso

model = Lasso(alpha=10)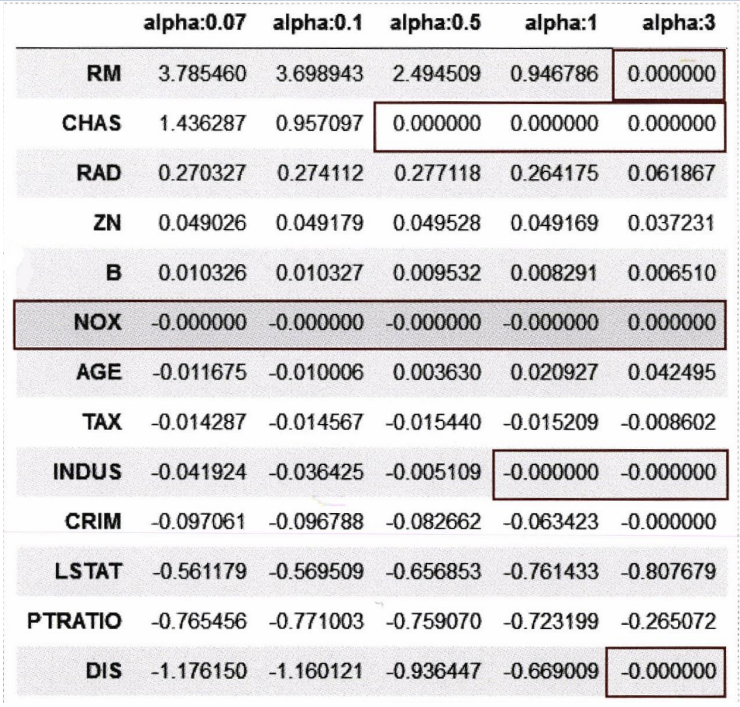

위 그림 역시 $\alpha$를 변경하며 회귀 계수를 확인해본 결과이다. $\alpha$를 높일 수록 더 많은 $W$가 0이 되는 것을 확인할 수 있다.

엘라스틱넷

엘라스틱넷은 L1 규제에 L2 규제를 더한 모델이다. L1 규제를 적용하면 불필요한 feature의 회귀 계수는 0으로 만드는데, 이 때 또 다른 feature의 회귀 계수가 급격히 커질 수도 있다. 따라서 이런 이슈를 해결하기 위해 L2 규제를 추가한 것이다.

[ 주요 파라미터 ]

• $\alpha$
  • 엘라스틱넷의 주요 파라미터는 L1, L2 규제와 동일하게 $\alpha$를 받는데, L1, L2 규제의 $\alpha$와는 약간 다르다. 엘라스틱넷의 $\alpha$는 L1 규제의 $\alpha$와 L2 규제의 $\alpha$의 합이다.
• l1_ratio
  • 이 파라미터는 간단한 계산이 필요하다. $\frac{a}{a+b}$으로 계산하는데, a는 L1 규제의 $\alpha$이고, b는 L2 규제의 $\alpha$이다.

엘라스틱넷도 L1, L2와 같이 sklearn.linear_model 모듈에 구현되어있으며 ElasticNet 클래스를 사용한다.

from sklearn.linear_model import ElasticNet

ElasticNet = Lasso(alpha=0.5)