다항회귀와 과대적합/과소적합 이해

지금까지는 독립변수가 한 개인 일차 방정식 형태의 회귀식만 봤다. 그런데 현실 세계는 하나의 직선으로 표현하기는 무리가 있으며 다항식으로 표현해야 한다. 따라서 회귀도 다항 회귀가 필요하다. 다항 회귀의 식은 다음과 같다.

$y = w_0 + w_1x_1 + w_2x_2 + \dots + w_nx_n$

회귀 방정식에서 변수가 하나 늘어난다는 것은 데이터의 차원이 높아진다는 의미이고, 결과에 대해 더 자세히 표현할 수 있게 된다. 아래 그림을 살펴보자.
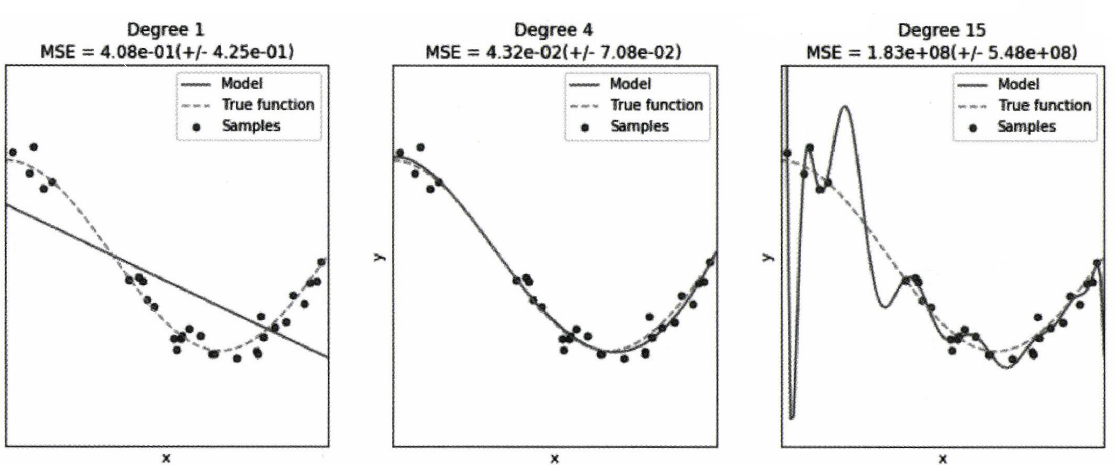그래프에서 점은 실제 관측된 데이터를 표현한 것이고(학습데이터) 점선은 우리가 찾고자 하는 회귀선이다. 왼쪽에서부터 feature의 개수가 1개, 4개, 15개이다. feature가 1개일 때에는 실제 데이터를 전혀 예측하지 못하고, feature의 개수가 늘어날 수록 점점 더 잘 예측하는 것을 볼 수있다. 하지만 feature가 15개처럼 너무 많을 때에는, 매우 잘 예측하지만 실제 회귀선에서 많이 벗어나있는 것을 볼 수 있다. 학습 데이터에 억지로 적합하게 하기 위해서 매우 큰 $W$가 설정된다.
위 그림에서 맨 왼쪽 그래프는 과소적합(underfitting), 맨 오른쪽 그림은 과대적합(overfitting)을 보여주고 있다.



모델의 예측값을 편향(bias)과 분산(variance)의 관점으로 살펴보면 다음과 같다.

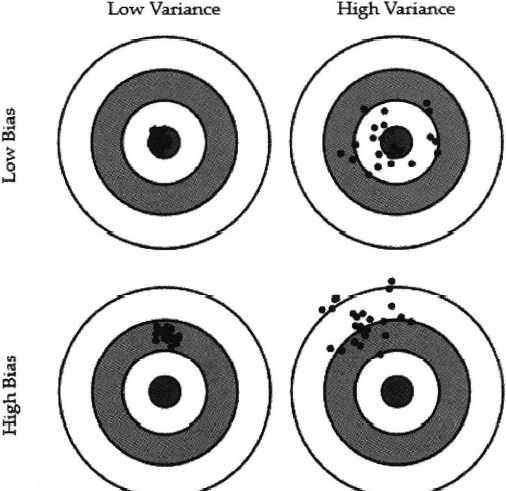
위 그림은 예측 결과를 과녁에 표현하고 있다. 행은 편향을, 열은 분산을 나타낸다. 편향과 분산의 의미는 아래와 같다.

• 편향은 정답값을 얼마나 잘 맞췄냐를 나타낸다. 정답값을 잘 맞추면 편향이 낮고, 잘 맞추지 못하면 편향이 높다.
• 분산은 예측의 결과가 일정하지 못하고 들쭉날쭉한지를 나타낸다. 결과를 잘 맞추는 것도 중요하지만, 일관되게 결과를 나타내는 것도 중요하다.

이어서 위 그림을 해석해보자. 편향이 낮다는 것은 과녁 중앙을 얼마나 잘 맞추느냐의 문제이다. 1행처럼 과녁 중앙에 예측값이 있다면 편향이 낮고, 2행처럼 과녁 중앙에서 많이 벗어나면 편향이 크다고 한다. 분산이 낮은것은 예측을 얼마나 일정하게 하는지의 문제이다. 1열처럼 예측 값이 일정하게 모여있다면 분산이 작다고 하고, 2열처럼 예측 값이 일정하지 않다면 분산이 크다고 한다.