PCA(Principal Coponent Analysis)

PCA는 대표적인 차원 축소 방법이다. 기본 원리는 정사영하는 것이다. 예를 들어 아래와 같이 몸무게와 키를 feature로 갖는 데이터가 있다고 하자.

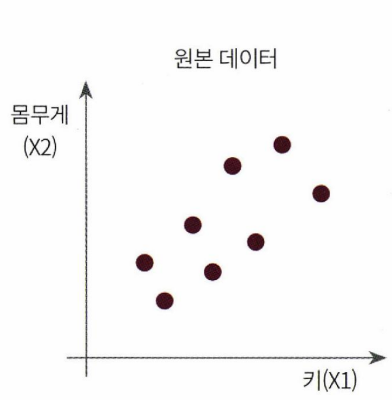
이 데이터의 변동성이 가장 큰 방향으로(편의상 북동쪽이라고 하겠다.) 축을 생성하고, 각 데이터를 새로 그린 북독쪽 축에 정사영한다. 그러면 원본 데이터 분포의 특징을 유지하면서 하나의 축으로 데이터가 축소되는 것이다.
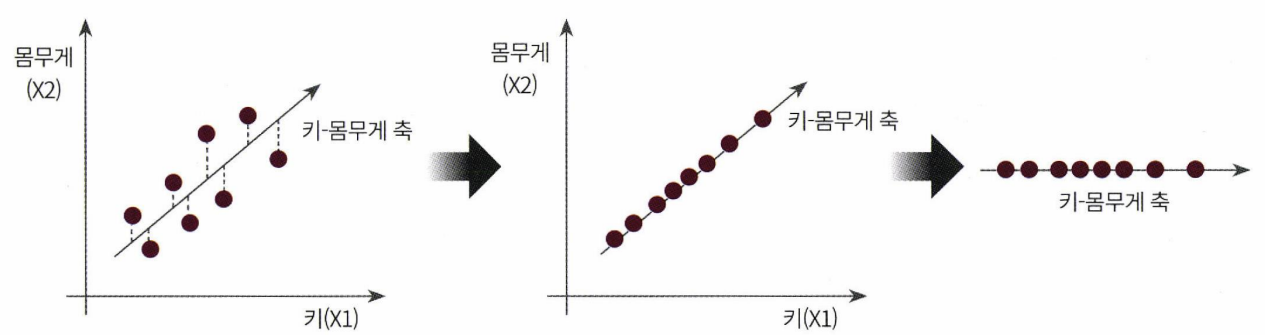
<이미치 출처 : 파이썬 머신러닝 완벽가이드>

여기서 중요한 것은 변동성이 가장 큰 방향으로 새로운 축을 생성한다는 것이다. 변동성이 가장 큰 방향으로 축을 생성하는 이유는, 데이터의 원래 분포를 최대한 유지하기 위함이다. 아래 그림을 살펴보자
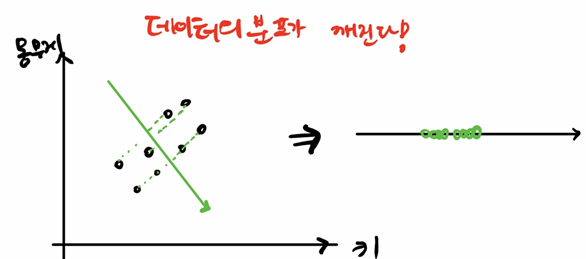변동성이 가장 큰 북동쪽이 아닌 남동쪽 방향으로 벡터를 생성하고 정사영했을 때에는 원본 데이터의 분포와 달라져 데이터의 특성이 변하게 된다. 따라서 변동성이 큰 축을 찾는 것이 가장 중요하다.

교재에서는 선형대수학도 가져와 PCA에 대해 설명한다. 내가 선형대수 관점에서의 PCA의 동작 방법을 이해한 것을 한 줄로 나타내면 아래와 같다.(선형대수를 거의 몰라 구글링을 계속하고, 책도 계속 읽어서 나름대로 이해한 결과다..)

입력되는 feature들의 공분산을 전부 구하고, 분산의 크기만을 분리하여 분산의 크기가 큰 순서대로 해당 변수를 주성분으로 선택하기

PCA는 각 feature들끼리 공분산을 구하여 공분산 행렬을 만든다. 교재의 예시와 같이 X, Y, Z 세 개의 변수를 feature로 같는 데이터셋을 가정하겠다.

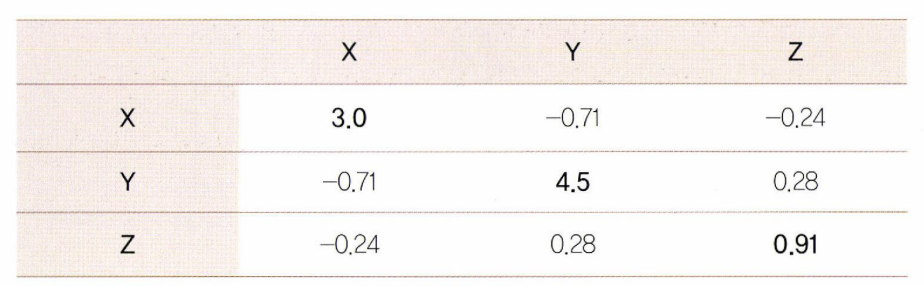공분산 행렬은 $n\times n$인 정방행렬이자 대칭행렬다.3개의 변수를 가지므로 $3\times 3$ 정방행렬이 나오고, 대각선 값들을 기준으로 원소값들이 대칭된다.

대칭행렬은 고유벡터와 고유값을 분해하는 데에 좋은 특성을 가지고 있는데, 고유벡터를 직교행렬로 대각화하고, 고유값을 정방행렬로 대각화 할 수 있는 성질이다.(사실 이 내용을 이해하지 못했다,,)

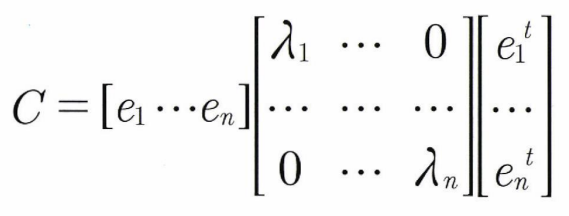따라서 공분산 C는 위와같이 변환된다고 한다. $e_{1}$는 가장 분산이 큰 방향을 가진 고유벡터이고, $e_{2}$는 $e_{1}$와 수직이면서 분산이 다음으로 큰 고유벡터이다. 따라서 PCA의 결과 $e_{1}$, $e_{2}$, $e_{3}$... 순으로 변수가 주성분으로 선택된다.

다른 sklearn의 모델들과 마찬가지로 PCA도 sklearn 패키지를 이용하면 쉽게 사용할 수 있다. PCA는 sklearn.decomposition 모듈 안에 있으며 사용 방법은 다른 스케일러와 같이 fit()과 transform()가 메서드로 존재한다. n_components 파라미터로 선택할 주성분의 개수를 지정한다.

아래 예시에는 별다른 데이터를 로드하지 않았으므로 원본 데이터는 data로, PCA의 결과는 pca_data로 받는다.

from sklearn.decomposition import PCA

pca = PCA(n_components=3)

pca.fit(data)
pca_data = pca.trainsform(data