LDA(Linear Discriminant Analysis)

LDA는 PCA와 비슷하게 데이터셋을 저차원으로 축소하는 방법이다. 중요한 차이는 LDA는 지도학습의 분류 문제에서 사용하기 쉽게 클래스 분별력을 유지하면서 차원을 축소한다.

PCA에서는 기초 행렬을 공분산 행렬로 설정한데 비해 LDA에서는 집단 간 분산과 집단 내 분산을 기초 행렬로 설정하여 고유벡터와 고유값을 분해한다.

[ 집단 내 분산과 집단 간 분산 ]
분류분석에서 클래스를 2차원 공간에 나타낸다고 가정해보자. 초록색 집단(군집)과 노란색 집단은 나눠져있고, 각 집단의 분산은 '집단 내 분산'이라고 표현한다. 위의 예시에서는 노란색 집단의 분산이 더 크다. 그리고 두 집단 간의 거리를 '집단 간 분산'이라고 한다. 군집분석을 할 때 집단 내 분산은 작게, 집단 간 분석은 크게 설정되도록 군집을 설정해야한다.

LDA를 식으로 나타내면 아래와 같다. 집단 내 분산 행렬을 $S_{W}$로, 집단 간 분산 행렬을 $S_{B}$로 하고, 고유벡터와 고유값을 분해할 수 있다.고유값이 가장 큰 순서대로 고유벡터를 선택하고, 선택된 고유벡터로 새로운 데이터를 변환한다.

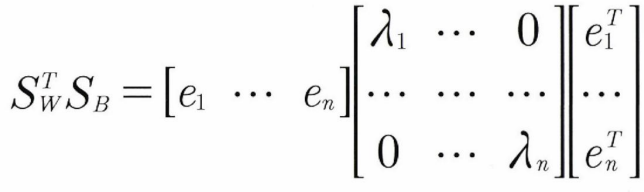
LDA는 sklearn.discriminanat_analysis 모듈에 있으며 사용 방법은 PCA와 동일하다. 하지만 중요한 것은, LDA는 지도학습 기반의 보델이기 떄문에 target을 연결해주어야 한다.(PCA는 비지도학습 기반의 모델이라서 feature만 입력하면 됨)

from sklearn.discriminant_analysis import LinearDiscriminanatAnalysys

lda = LinearDiscriminanatAnalysys(n_components=3)
lda.fit(data)
lda_data = lda.transform(data)

SVD(Singular Value Decomposition)

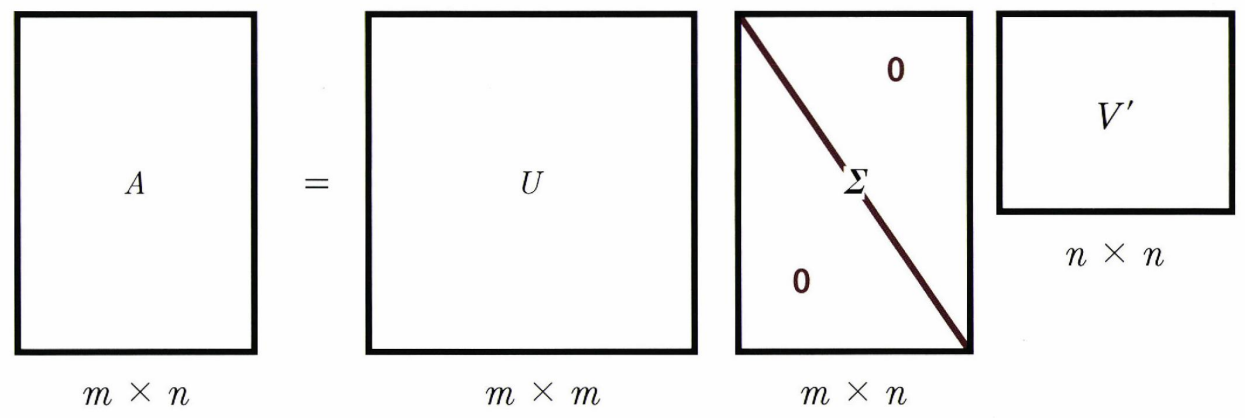
SVD도 PCA와 같이 행렬에서 고유벡터와 고유값을 분해하는 방법이다. 그런데 PCA나 LDA는 정방행렬($n\times n$)만을 분해할 수 있다면, SVD는 $m\times n$ 크기의 행렬을 분해할 수 있다. 행렬을 A라고 하면 다음과 같이 분해할 수 있다.

$A = U Σ V^T$

SVD는 numpy.linalg.svd 클래스로 구현되어있다.

import numpy as pd
from numpy.linalg import svd

data = np.random.randn(4, 4) # 4x4 행렬 생성
U, Sigma, Vt = svd(data) # 고유벡터, 시그마, 고유값으로 분해

(사실 SVD 유도 부분은 부분은 내가 이해를 잘 하지 못해서 선형대수를 공부한 후 내용을 추가하겠다.)

NMF(non-Negative Matrix Factorization)

NMF는 원본 행렬의 모든 원소값이 양수라면, 두 개의 기반 양수 행렬로 분해될 수 있다.
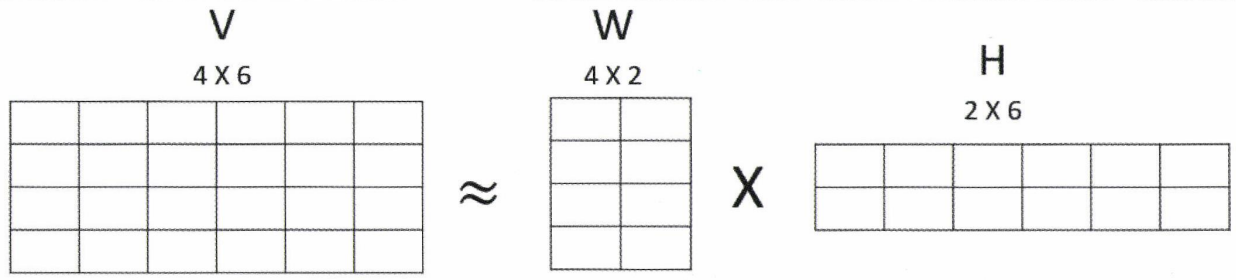위와 같이 $4\times 6$인 행렬 $V$는 $4\times 2$인 행렬 $W$과 $2\times 6$인 행렬 $H$로 분해될 수 있다. $W$는 원본 행렬에서 행에 대한 잠재요소의 값이 얼마나 되는지를 나타내고, $H$는 원본 행렬에서 열에 대한 잠재요소의 값을 나타낸다. NMF는 sklearn.decomposition 모듈에 구현되어있으며 다른 sklearn의 모델들과 같이 fit(), transform()을 사용할 수 있다.

from sklearn.decomposition import NMF

nmf = NMF(n_components=3)

nmf.fit(data)
nmf_data = nmf.transform(data)

< 총평 >
선형대수에 대한 개념이 많이 부족한 것 같다. 선형대수 공부를 어느 정도 병행해야 할 것 같다.