DFS 구현
DFS는 깊이 우선 탐색의 줄임말로 그래프 중 깊은 곳을 먼저 탐색하는 방법이다. 그래프를 표현하는 방식은 인접 행렬, 인접 리스트 방법이 있다. DFS를 구현할 때에는 스택 구조를 사용하는 것이 일반적이다. 그래서 이번 실습에서는 스택과 재귀함수로 각각 구해보도록 하자.
일반적으로 동일한 레벨에 방문해야하는 노드가 두 개 이상 있을 때, 숫자가 작은 순서대로 방문한다. 이 점을 유의하며 구현을 해보자.
인접 행렬
구현에 사용될 데이터는 아래와 같다.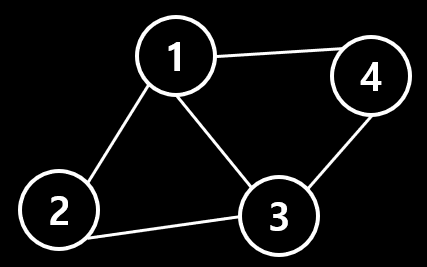
# 인접 행렬 - 행렬과 노드 별 방문 여부를 나타내는 리스트
matrix = [
[0, 0, 0, 0, 0],
[0, 0, 1, 1, 1],
[0, 1, 0, 0, 1],
[0, 1, 0, 0, 1],
[0, 1, 1, 1, 0]]
visited = [False] * len(matrix)Stack으로 구현
# stack으로 구현
def dfs_matrix_stack(matrix, start_node, visited) :
need_to_visit, result = list(), list() # 확인해야 하는 노드를 담을 리스트와 결과 리트스
need_to_visit.append(start_node) # 시작 노드 추가
while need_to_visit : # 확인해야 하는 노드가 없을 떄까지 반복
node = need_to_visit.pop() # 현재 방문 중인 노드
if not visited[node] : # 이 노드에 방문한 적이 없다면
visited[node] = True # 방문 기록 남기기
result.append(node)
for i in range(len(matrix[node])-1, 0, -1) : # 작은 수부터 돌아야 하므로 뒤에서 앞으로 반복
if matrix[node][i] == 1 and not visited[i] : # 현재 노드와 연결되어있고 그 노드가 방문한 노드가 아니라면
need_to_visit.append(i) # 이 노드도 돌아야 하므로 돌아야 하는 노드에 추가
return result
dfs_matrix_stack(matrix, 1, visited)# 결과
[1, 2, 4, 3]처음에 이해하기 어려웠던 점은 range(len(matrix[node]) -1, 0, -1)이다. 리스트를 뒤에서부터 도는 이유는 stack의 특성 때문인데, pop()은 리스트에서 가장 뒤에 있는 원소를 추출하기 때문이다. 만약 뒤로 반복하지 않는다면, pop()의 결과가 큰 수부터 나오게 될 것이다.(이해가 안되면 need_to_visit에 원소가 추가되고 나가는 순서를 손으로 써보자)
재귀함수로 구현
# 재귀함수로 구현
result = list() # 결과를 담을 리스트
def dfs_matrix_recursive(matrix, start_node, visited, result) :
result.append(start_node) # 시작 노드 추가
visited[start_node] = True # 시작 노드에 접근 기록
for i in range(len(matrix[start_node])) : # 현재 노드와 인접한 모든 노드를 반복
if matrix[start_node][i] == 1 and not visited[i] : # 현재 노드와 인접해있고, 방문한 기록이 없는 노드일 때
dfs_matrix_recursive(matrix, i, visited, result) # 그 노드에 대해 dfs 함수를 또 적용
return result
dfs_matrix_recursive(matrix, 1, visited, result)# 결과
[1, 2, 4, 3]재귀함수는 결과를 다음 반복으로 결과 리스트도 넘겨야하기 때문에 인자로 결과 리스트를 추가해주어야 한다. 현재 제공받은 인접 행렬에서 현재 방문한 노드의 행을 처음부터 반복하며 인접 여부를 판단해야하기 때문에 이번에는 반복을 그대로 돌렸다.(이것도 헷갈리면 손으로 써보기)
인접 리스트
구현에 사용되는 데이터는 아래와 같다.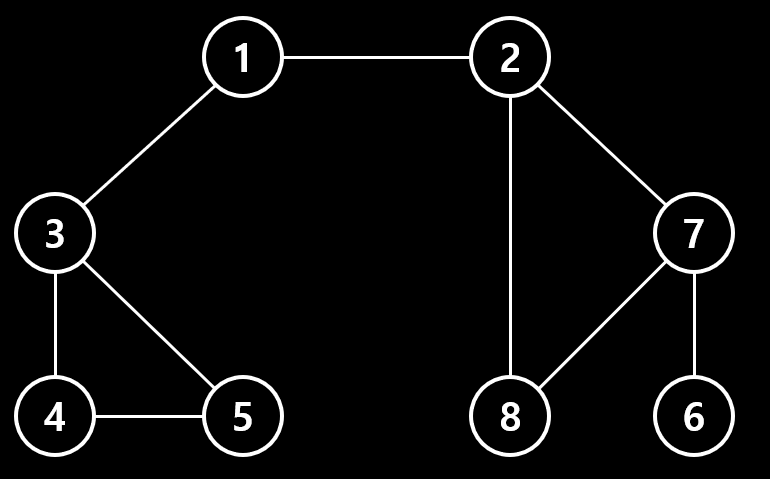
# 인접 리스트 - 노드는 인덱스가 1부터 시작하므로 첫 번쨰 요소는 빈 리스트를 넣음
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]Stack으로 구현
# stack으로 구현
def dfs_list_stack(graph, start_node) :
need_to_visit, visited = list(), list() # 확인해야 하는 노드를 담을 리스트와 결과 리트스
need_to_visit.append(start_node) # 시작 노드 추가
while need_to_visit : # 확인해야 하는 노드가 없을 때까지 반복
node = need_to_visit.pop() # 현재 방문 중인 노드
if node not in visited : # 이 노드에 방문한 적이 없다면
visited.append(node) # 방문기록 남기기
need_to_visit.extend(graph[node][::-1]) # 작은 숫자를 먼저 돌게 하기 위해 리스트 순서를 바꿔서 저장
return visited
dfs_list_stack(graph, 1)# 결과
[1, 2, 7, 6, 8, 3, 4, 5]인접 행렬과 그리 다르지 않다. 확이냏야 하는 노드와 현재 노드 간의 관계를 생각하며 코드를 보면 이해가 더 쉬울 것이다. 이 때도 작은 숫자를 먼저 확인할 수 있게 확인해야할 노드를 추가할 때 그 순서를 바꿔주었다.([ : : -1] 사용)
재귀함수로 구현
# 재귀함수로 구현
visited = list()
def dfs_list_recursive(graph, start_node, visited) :
visited.append(start_node)
for node in graph[start_node]: # for문은 원소를 앞에서 부터 돌기 때문에 [::-1] 필요 없음
if node not in visited :
dfs_list_recursive(graph, node, visited)
return visited
dfs_list_recursive(graph, 1, visited)# 결과
[1, 2, 7, 6, 8, 3, 4, 5]이 부분에서는 인접 행렬과 마찬가지로 확인할 원소는 오름차순 정려되어 있기 때문에 [ : : -1]을 하지 않아도 된다.
참고한 사이트