1. 통계량
1-1. 통계량 이란?
데이터의 분포를 시각적으로 표현하기만 해서는 데이터의 특성을 정확히 파악할 수 없다. 따라서 우리는 데이터의 특징을 수치로 변환하여 파악하는 방법이 필요하다. 데이터의 특징을 수치로 변환한 것을 기술통계량(=요약통계량)이라고 한다. 기술통계량은 주로 양적 변수(=수치형 변수)를 대상으로 계산한다.
1-2. 기술통계량 종류
중요한 점은 기술통계량은 모집단의 특성을 파악한 것이 아닌 표본에 대한 성질이다. 모집단은 앞서 말한대로 파악하기 어려워 표본들의 특성으로 추정하게 되는데, 통계량을 모집단의 추정에 사용되는 수치들로 생각해도 좋다.
1) 대표값
대표값은 데이터의 특성을 나타내는 수치들 중에서, 데이터 분포의 위치를 나타내며, 데이터를 대표할 수 있는 값을 정량화 하기 위해 사용한다.
-
평균(mean)
표본에서 얻었으므로 표본평균이라고도 한다. 아래와 같이 구한다.평균은 이상치의 영향을 크게 받는다. 다른 데이터보다 월등히 크거나 작은 데이터가 몇개 있으면 평균은 어느새 이상치가 있는 방향으로 이동하기 때문이다.
-
중앙값(median)
중앙값은 크기 순으로 나열했을 때 중간에 오는 값을 의미한다. 값의 크기보다 순서에 집중하기 때문에 이상치가 있어도 크게 영향을 받지 않는다. 아래 예시를 보자.[ 이상치에 대한 영향 - 평균과 중앙값 ]
집합 1 : {1, 2, 3, 100}
집합 2 : {1, 2, 3, 4, 5}집합 1과 2의 평균은 각각 26.5, 3이다. 반면 중앙값은 두 집합 모두 3이다. 이와 같이 중앙값은 평균보다 이상치의 영향이 작다.
-
최빈값(mode)
최빈값은 이름 그대로 가장 빈번하게 나온 수이다. 이산형 변수는 값이 나눠져있기 때문에 그 라벨 값을 구하면 되지만, 연속형 변수는 그렇지 않다. 따라서 연속형 변수의 최빈값을 구할 때에는 히스토그램처럼 일정 범위를 정한 후 그 범위 안의 데이터 개수를 샌다.
데이터 분포의 좌우 대칭성을 나타내는 왜도(=skewness)가 있다.(뒤에 나옴) 아래 사진은 왜도에 따라 평균, 중앙값, 최빈값이 달라지는 모습을 나타낸 것이다.
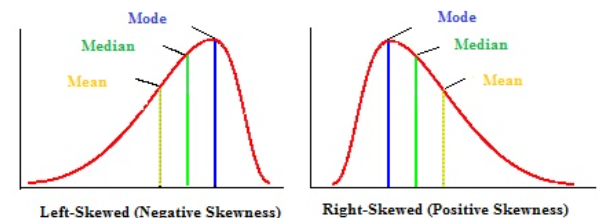 출처 : 왜도에 따른 통계량 변화
출처 : 왜도에 따른 통계량 변화
2) 분산과 표준편차
대표값을 사용하면 분포의 대략적인 위치는 알 수 있지만 데이터가 얼마나 흩어져있는지에 대한 정보는 알 수 없다. 따라서 데이터의 퍼짐을 나타내는 분산과 표준편차에 대해 알아보자.
- 분산(Variance)
분산은 표본에서 얻은 것임을 나타내기 위해 표본분산이라고도 한다. 분산은 '편차 제곱의 평균'으로 구한다.분산의 성질은 아래와 같다.[ 분산의 성질 ]
-
- 모든 값이 같다면,
- 데이터의 퍼짐 정도가 크다면 값이 큼 - 표준편차(standard deviation)
분산은 데이터의 퍼짐 정도를 측정할 수 있어 중요한 지표이다. 그런데 편차에 제곱을 하므로 그 값을 현실적으로 해석하기 어렵다. 예를 들어 단위의 데이터에 분산을 구한 경우 분산의 단위는 가 되기 때문이다. 따라서 단위를 맞춰주기 위하여 분산에 루트를 씌워주고, 그것을 우리는 표준편차라고 한다. 표준편차 역시 표본에서 얻은 것임을 나타내기 위해 표본표준편차라고도 한다.
3) 4분위수와 상자그림(box plot)
데이터를 오름차순으로 정렬한 후 25%되는 지점씩 끊는다. 각 점을 Q1, Q2, Q3로 설정한다. Q2는 50%지점이므로 중앙값과 같다. 사분위 범위(IQR)은 Q3-Q1으로 구하고, IQR은 이상치를 판단하는 기준이 된다.
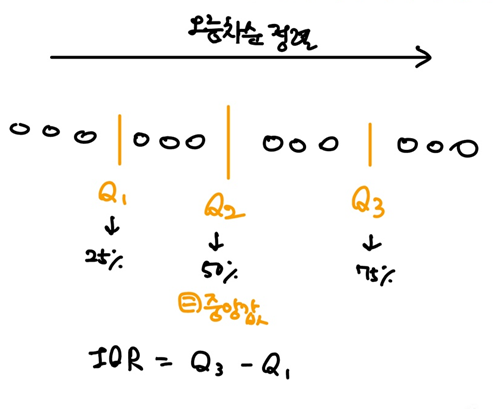
4분위수를 그래프로 나타내면 상자그림(box plot)이다.
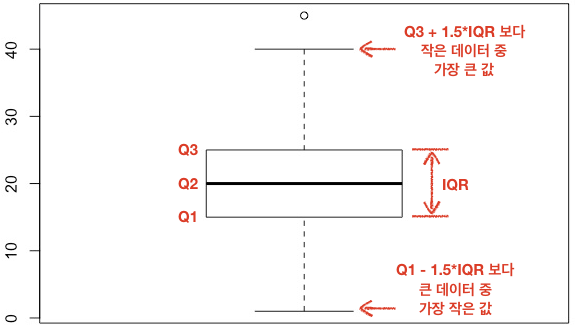
상자그림은 4분위수와 IQR을 사용하여 이상치를 판단하는 방법이다. 정상 데이터의 범위는 ~ 이다. 즉 이 범위를 벗어나는 데이터는 이상치로 판단한다.