1. 확률

1-1. 확률이란?

1) 확률과 확률변수

확률이란 발생 여부가 불확실한 사건에 대하여 발생 가능성을 숫자로 표현한 것이다. 확률을 표기할 때에는 'P(사건) = 확률' 형태로 표기한다. 확률은 실수로 표현한다.

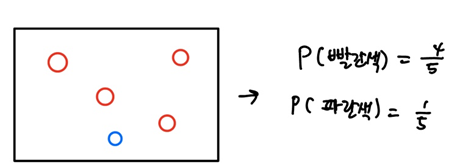
위 그림은 아래와 같이 표현할 수 있다.

위와 같이 $X$에 따라 확률이 달라지는 변수를 확률변수라고 한다. 그리고 확률변수가 실제로 갖는 값을 실현값이라고 한다.

2) 확률분포

확률분포는 x축에 확률변수, y축에 실현값을 표시한 분포이다. 위 예시를 확률분포로 그리면 아래와 같다.

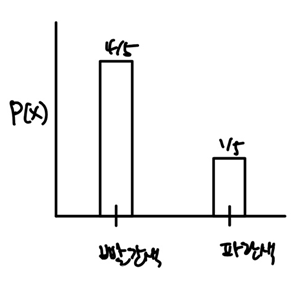
그런데 확률분포는 데이터 형태에 따라 조금 달라진다. 이산형 변수나 범주형 변수는 위와 같이 히스토그램으로 그려진다. 그런데 연속형 변수는 아래와 같이 그리며, 확률밀도함수라고 부른다.

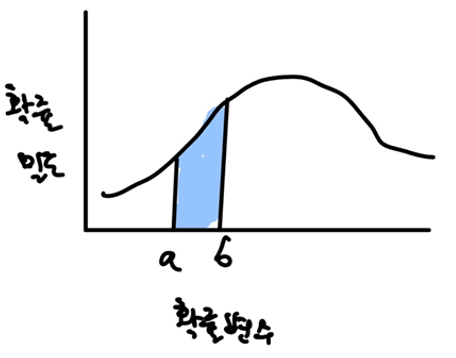
확률밀도함수는 특정 범위를 적분하여 나온 넓이를 확률로 사용한다.

1-2. 추론통계와 확률분포

1) 통계학에서 확률분포가 중요한 이유

통계학에서 관심이 있는 대상은 모집단이다. 그런데 현실세계에서 모집단은 구할 수 없으므로 일부 표본으로 모집단의 성질을 추정하는 방법을 사용한다.

이런 관계를 수학으로 끌고오면, 모집단을 특정한 확률분포로 가정하고, 표본은 그 확률분포에서 생성된 실현값으로 가정하여 분석한다.

현실 세계	→	수학세계
모집단	→	확률분포
표본집단	→	실현값

결국 수학적으로 계산을 하기 위해 현실을 확률로써 치환하는 것이다.

※ 주의! 3.3 통계량에 나온 수치들은 표본에 대한 값들이다. 지금부터 나오는 수치들은 확률분포에 대한 특성값들이기 때문에 모집단에 대한 값들이다! 헷갈리지 않게 주의하자

2) 기댓값(=E(X))

양적 확률변수(=수치형)이라면, 확률분포를 특징지을 수 있는 수치를 계산할 수 있다. 그 중 변수가 확률적으로 얼마나 발생하기 쉬운지를 나타내는 기댓값이 있다. 기댓값을 구하는 방법은 변수의 데이터 타입에 따라 달라지는데 중요한 점은 어떤 변수던 키 포인트는 $x \times P(x)$라는 점이다.

[ 이산형 변수 기댓값 ]

$E(X) = \Sigma_{i=1}^k \; x_i P(X=x_i)$

[ 연속형 변수 기댓값 ]

$E(X) = \int \; xf(x)\;dx$

3) 분산(V(X))과 표준편차($\sigma$)

확률분포가 기댓값 주변에 어느정도 퍼져있는지는 분산으로 표기한다. 기술통계량에서 나온 분산과 마찬가지로 편차 제곱의 평균으로 구한다.

[ 이산형 변수 분산 ]

$V(X) = \Sigma_{i=1}^k(x_i - E(X))^2 \; P(X=x)$

[ 연속형 변수 분산 ]

$V(X) = \int(x-E(X))^2f(x)\;dx$

분산에 제곱근을 씌우면 표준편차이다.

4) 왜도(skewness)와 첨도(kurtosis)

왜도는 확률분포가 좌우 대칭 여부를 나타내고, 첨도는 확률분포가 얼마나 뾰족한지를 나타낸다.

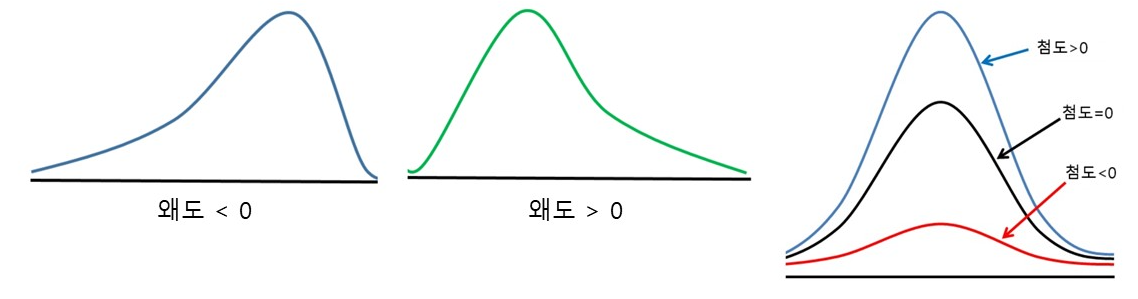
출처 : 왜도와 첨도

2. 동시확률분포

2-1. 두 개의 확률분포

1) 독립의 개념

지금까지 살펴본 확률분포는 확률변수 1개만 고려한 내용이다. 확률변수를 2개를 동시에 고려할 때 동시확률분포 $P(X, Y)$라고 표현한다.

2개의 확률 변수를 다룰 때에는 독립이 중요한 개념이다. 독립이란 사건 X의 발생이 Y에 영향을 미치지 않고, 사건 Y의 발생이 X에 영향을 미치지 않는 관계이다. 한 사건이 어떤 결과이던 다른 사건이 발생할 확률에 영향이 없는 관계를 말한다.

독립사건의 확률은 두 확률을 곱하여 구한다.

[ 독립 사건 ]
사건 X, 사건 Y가 독립일 때, $P(X, y) = P(X) \times P(Y)$이다.

2) 조건부 확률

두 사건이 독립이 아닌 경우 조건부 확률이라고 부른다. X의 발생이 Y의 확률에 영향을 미치거나 그 반대의 경우이다.

X에 따른 Y의 확률은 $P(Y|X)$로 표현한다.