1. 추론통계를 배우기 전에 알 것들

우리가 알기 원하는 데이터 집단은 모집단이다. 그런데 보통 모집단은 그 크기가 매우 크고 자주 변해서 모집단을 전수조사 하기란 쉽지 않다. 그래서 우리는 모집단에서 데이터 일부분을 뽑아(=표본) 성질을 파악하므로서 모집단을 추정하는 방법을 채택했다. 이를 추론통계라고 한다.

1-1. 모집단과 표본 = 확률분포와 실현값

앞 장에서 배운 확률분포와 실현값에 대해 생각해보자. 확률분포는 가로축에 확률변수 값을, 세로축에 확률을 나타낸 분포였고 실현값은 그 확률분포를 따르는 특정한 값이다. 확률분포와 실현값은 모집단과 표본의 관계와 비슷하다는 것을 알 수 있다. 우리는 수학적으로 계산하기 위해 보집단은 확률분포로, 표본은 실현값으로 생각할 수 있다.

따라서 통계학의 목표는 아래와 같이 바뀔 수 있다.

"표본으로 모집단을 추정한다" ⇒ "실현값으로 확률분포를 추정한다"

1-2. 모형화

현실적으로 데이터를 얻어보면 그 분포가 들쭉날쭉하고 수학적으로 다룰 수 없는 경우가 많다. 따라서 이를 수식으로 바꾸면 모집단의 추정이 용이해진다. 모집단을 수학적인 확률분포로 근사하는 것을 모형화라고 한다.

1-3. 편향과 표본 추출 방법

모집단에서 표본을 뽑을 때 중요한 점은 무작위 추출로 이루어져야 한다는 점이다. 또한 한 번의 표본 추출이 다음 번의 표본 추출에 영향을 미치지 않아야 한다.(=독립이어야 함)

표본을 추출하는 방법은 아래와 같다.

• 단순 임의 추출 : 난수를 설정해 완전 무작위로 표본을 선택하는 방법
• 계통 추출 : 모집단 데이터들을 일렬로 늘여놓고 K번째마다 추출해 표본 선택
• 층화 추출 : 모집단에서 클래스별로 나눈 후, 그 비율대로 표본 추출
• 군집 추출 : 모집단에서 인접한 데이터끼리 임의로 하나의 군집으로 나눈 후 군집을 임의로 선택

이 중 가장 많이 사용하는 방법은 층화 추출 방법이다.

2. 추론통계를 직감적으로 이해하기

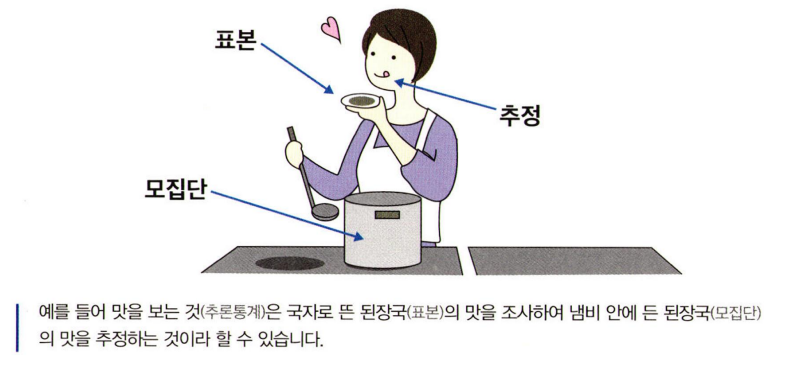
국을 요리할 때 간을 맞추기 위해 한 국자 떠서 맛을 본다. 이는 추론통계 과정과 일치한다.

1. 간이 맞는지 정말 알고자 하는 대상은 한 국자가 아니라 국 전체이다.
   ⇒ 통계학에서 정말 알고자 하는 것은 표본이 아니라 모집단이다.

2. 냄비 안의 국을 다 먹고 간이 맞는지 조사하는 것은 어렵다.
   ⇒ 모집단을 전수조사 하는 것은 거의 불가능하다.

3. 한 국자 떠서 먹어보는 것으로 간을 얼추 확인할 수 있다. 다만 국자가 아니라 한 숟가락인 경우에는 맛이 제대로 느껴지지 않아 간을 맞출 수 없다.
   ⇒ 작은 표본으로도 모집단을 추론할 수 있다. 다만 표본이 너무 적으면 모집단을 추론 할 수 없다.

4. 국자로 뜨기 전에 잘 섞어야 한다.
   ⇒ 표본은 편향되지 않아야 한다.