1. 이론적인 확률분포

1-1. 파라미터(=모수) 개요

이론적인 확률분포는 수식으로 표현되며, 그 형태를 정하는 파라미터(=모수)를 갖는다. 따라서 모수를 알면 확률분포의 형태를 알 수 있다.

통계의 목적은 모집단의 성질을 파악하는 것이었다. 모집단을 "어떤 특성을 가진 확률분포"라고 표현할 수 있다면, 모집단을 알게 되는 것이므로 통계에서 가장 중요한 부분이다.

1-2. 확률분포 종류

1) 정규분포(normal distribution)

정규분포는 가우시안 분포(Gaussian distribution)이라고도 한다. 정규분포의 모습은 아래와 같다.

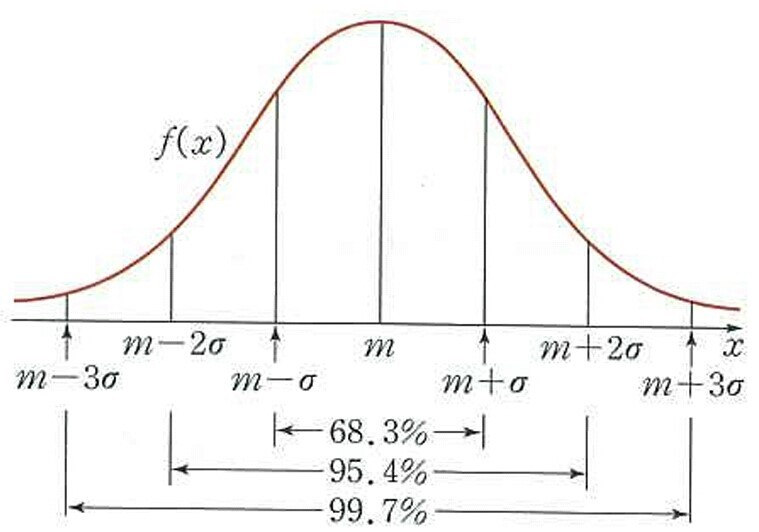
출처 : 정규분포

연속형 변수를 대상으로 정의되며 확률밀도함수는 아래와 같다.

정규분포의 형태를 결정하는 모수로는 $\mu$와 $\sigma$가 있으며 $N(\mu, \sigma)$로 표현한다.

특히 $\mu=0\;$, $\sigma=1$인 정규분포는 표준정규분포라고 한다. 일반 정규분포를 표준정규분포로 바꾸는 것을 표준화(standardizing)라고 하며 변환된 값을 $z$값이라고 부른다. 표준화 방법은 아래 식과 같다.

정규분포는 독특한 특징을 갖는다.

• 평균을 중심으로 종형이며 좌우 대칭이다.
• 평균 주변에 데이터 수가 가장 많고 평균에서 멀어질수록 데이터 수가 적어진다.
  • $\mu - \sigma$ ~ $\mu + \sigma$안에 데이터가 있을 확률은 68%
  • $\mu - 2\sigma$ ~ $\mu + 2\sigma$안에 데이터가 있을 확률은 95%
  • $\mu - 3\sigma$ ~ $\mu + 3\sigma$안에 데이터가 있을 확률은 99%
• 현실 세계에서 정규분포로 근사할 수 있는 현상이 많이있다.

2) 기타 확률분포

통계학에서 중요한 확률분포는 아래와 같다.

• 이산형 변수
  • 균등분포
  • 이항분포
  • 포아송분포
• 연속형 변수
  • 균등분포
  • 지수분포
  • 가우스 분포
• 검정통계량
  • t분포
  • F분포
  • $x^2$분포