2-3 트리

균형 이진 탐색 트리의 일종으로, 각 노드가 2개 또는 3개의 자식을 가질 수 있는 트리 구조이다. 이 트리는 항상 균형을 유지하여 탐색, 삽입, 삭제 등의 연산이 효율적으로 수행되도록 보장한다.

노드의 종류

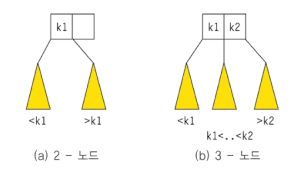
• 2-노드: 이진탐색트리처럼 하나의 데이터 K1와 두 개의 자식 노드를 가진다
• 3-노드: 2개의 데이터 k1, k2와 3개의 자식 노드를 가진다.
  

키 정렬

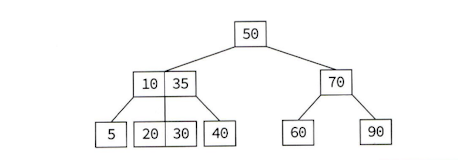
• 각 노드의 키들은 항상 정렬되어 있음
• 왼쪽 서브 트리에 있는 데이터들은 모두 k1보다 작은 값이다.
• 중간 서브 트리에 있는 값들은 모두 k1보다 크고 k2보다 작다
• 오른쪽에 있는 데이터들은 모두 k2보다 크다

삽입

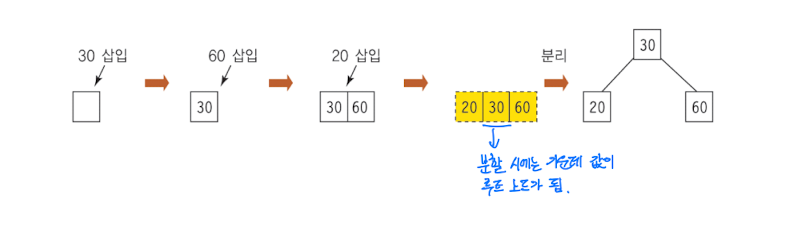
• 새 키를 삽입할 때, 노드가 꽉 차지 않은 경우에는 단순히 추가한다.
• 노드가 꽉 찬 경우(3-노드에 추가하려는 경우)

1. 노드를 분할하여 두 개의 2-노드로 만든다.
2. 중간 키를 부모 노드로 올린다.

• 이 과정에서 트리의 균형이 유지되며, 원래의 이진 트리 형태로 바뀐다.
• 노드가 분리되는 과정은 아래의 3가지로 나누어진다.

1. 단말 노드를 분리하는 경우
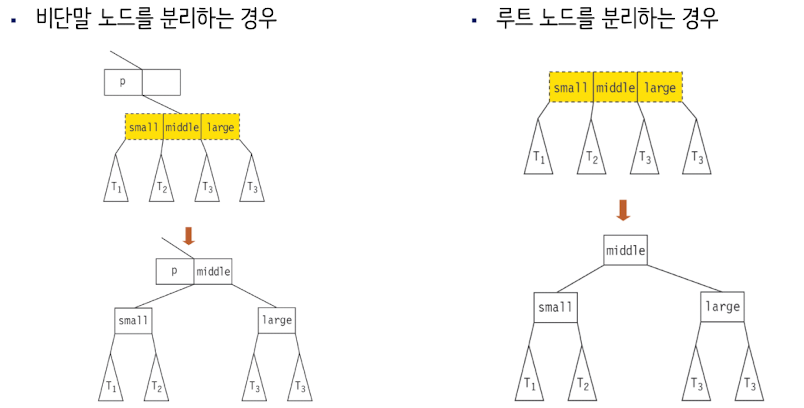
2. 비단말 노드를 분리하는 경우
3. 루트 노드를 분리하는 경우

단말 노드를 분리하는 경우

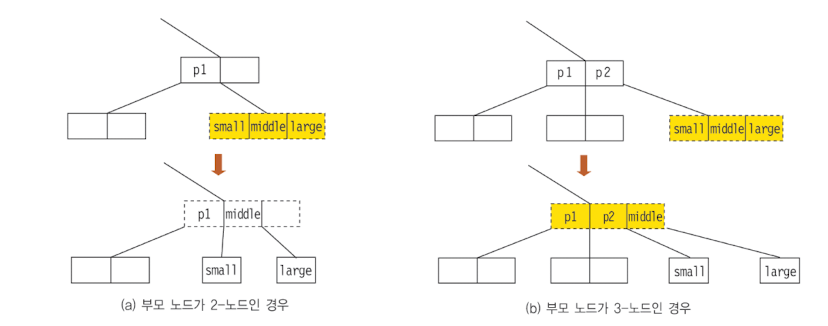
비단말 노드와 루트 노드를 분리하는 경우

장점과 단점

장점

1. 균형 유지: 항상 균형을 유지하므로 최악의 경우에도 성능이 $O(logn)$로 보장됨
2. 구현 단순성: 다른 균형 트리보다 구현이 비교적 단순

단점

1. 공간 낭비: 각 노드가 두 개 또는 세 개의 자식을 가질 수 있으므로, 비효율적인 메모리 사용 가능
2. 복잡한 삽입/삭제: 단순한 이진 탐색 트리보다 삽입 및 삭제 로직이 더 복잡하다.

출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구