알고리즘
1.LPT: Longest Processing Time first

머신 스케쥴링이란 모든 기계를 가동시켜 가장 최소의 시간 안에 작업들을 모두 끝내기 위한 것을 말한다. 이 문제는 알고리즘 분야에서 상당히 유서 깊은 문제로 많은 응용 분야를 가지고 있는데, 예를 들어 서버가 여러 개 있어 서버에 작업을 분배할 때도 사용할 수 있다.분
2.허프만 코딩(Huffman Coding)
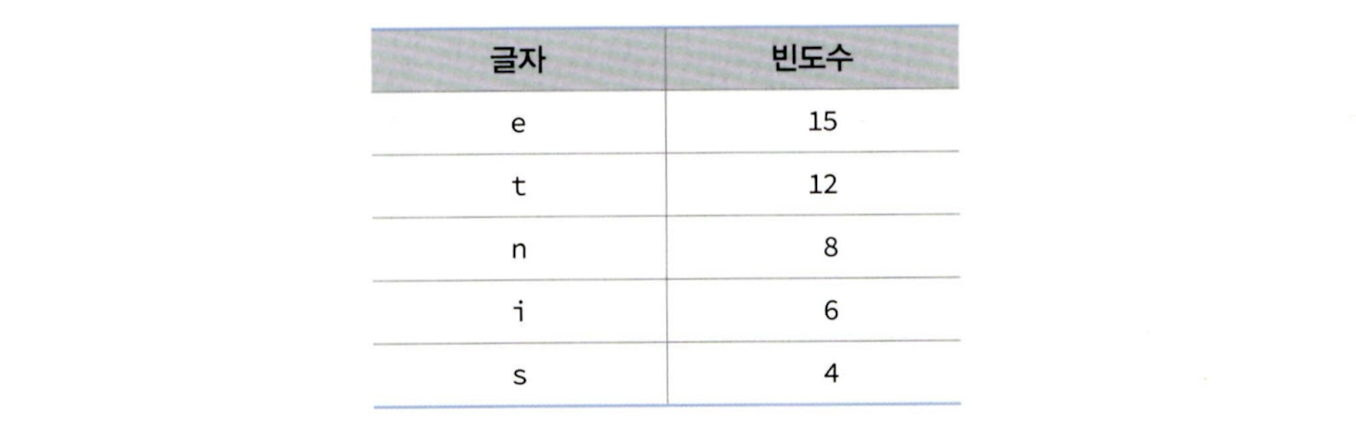
이진 트리는 각 글자의 빈도가 알려져 있는 메시지의 내용을 압축하는데 사용될 수 있다. 이런 특별한 종류의 이진트리를 허프만 코딩 트리라고 부른다.빈도수를 구하는 이유는 가변 길이의 비트열을 사용하기 위함이다. 빈도수가 가장 많은 글자에는 짧은 비트열을 사용하고, 잘
3.그래프의 탐색 - DFS(Depth first search)
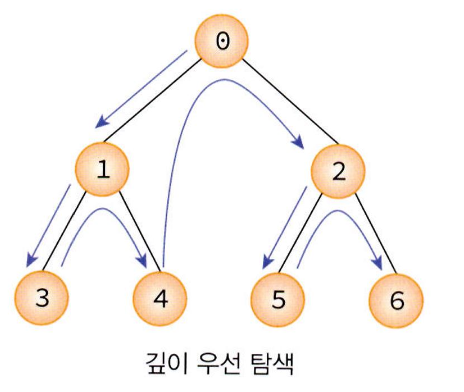
DFS는 트리에서 이해하면 쉽다.(트리도 그래프의 일종이기 때문) 트리를 탐색할 때 시작 정점에서 한 방향으로 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.위 그림에서 탐색 순서는 0→1
4.그래프의 탐색 - BFS(Breath first search)
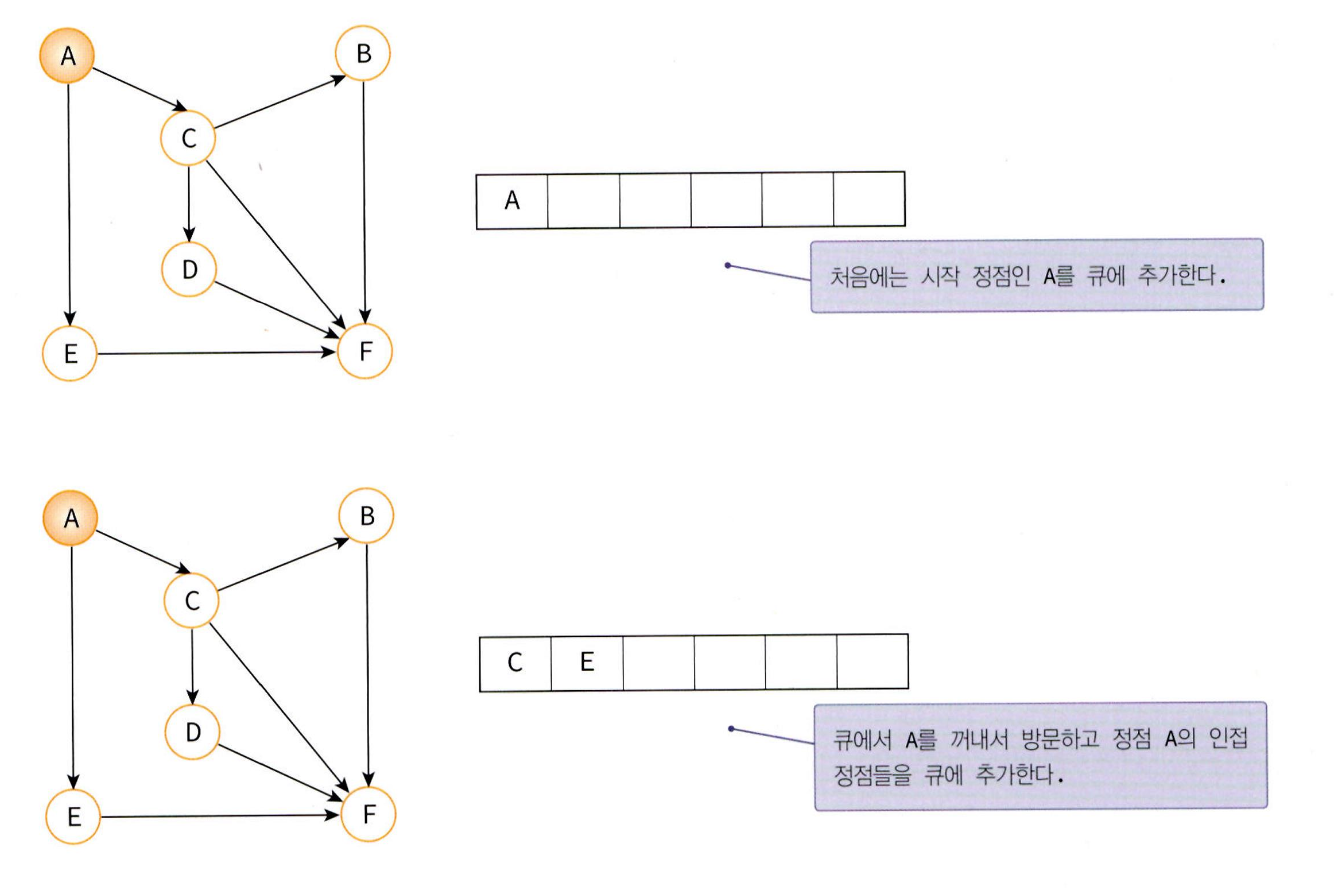
BFS는 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 탐색이다.BFS를 구현할 때는 큐(queue)를 사용하는데, 가까운 거리에 있는 정점들을 차례로 저장한 후 꺼낼 수 있는 자료구조로 큐가 적합하기 때문이다.알고리즘을 간략히
5.최소 비용 신장 트리(MST: Minimum Spanning Tree)
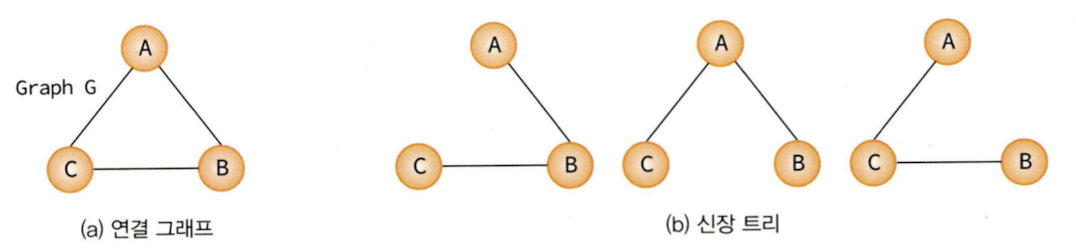
그래프 내의 모든 정점을 포함하는 트리로, 그래프의 최소 연결 부분 그래프가 된다. n개의 정점을 가지는 그래프의 신장트리는 n-1개의 간선을 가진다.DFS와 BFS로 구한 신장 트리는 오직 하나로 유일하다.최소 비용 신장 트리는 네트워크에 있는 모든 정점들을 가장 적
6.최단 경로(Shortest Path)
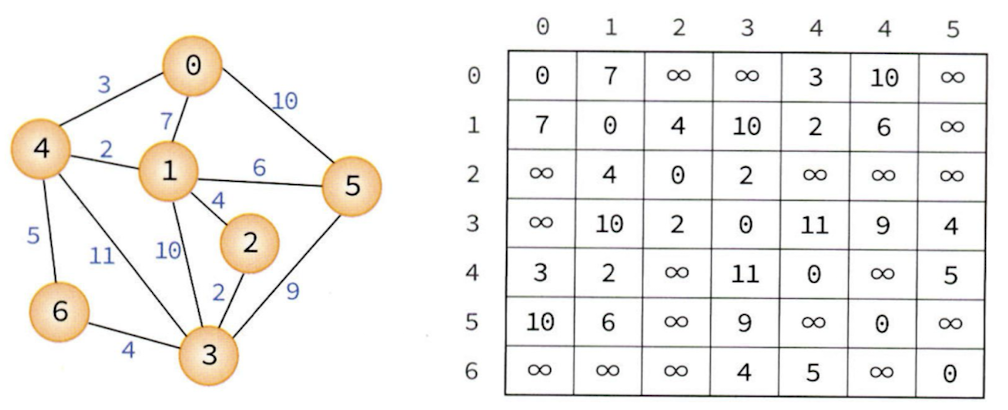
최단 경로 문제는 네트워크에서 정점 i와 정점 j를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제이다. 간선의 가중치는 비용, 거리, 시간 등을 나타낸다.예를 들어 위 그래프에서 정점 0에서 점점 3으로 가는 최단 경로는 0,4,1,2,3 이
7.최단 경로(Shortest Path)
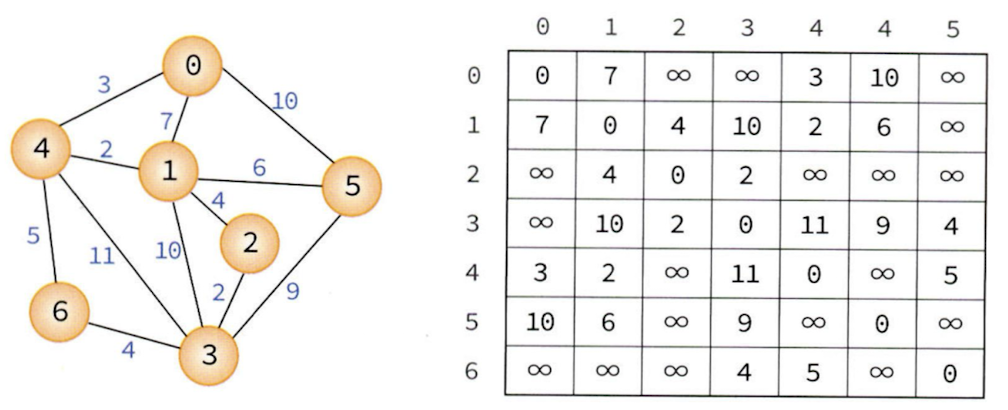
최단 경로 문제는 네트워크에서 정점 i와 정점 j를 연결하는 경로 중에서 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제이다. 간선의 가중치는 비용, 거리, 시간 등을 나타낸다.예를 들어 위 그래프에서 정점 0에서 점점 3으로 가는 최단 경로는 0,4,1,2,3 이
8.위상 정렬(Topological Sorting)
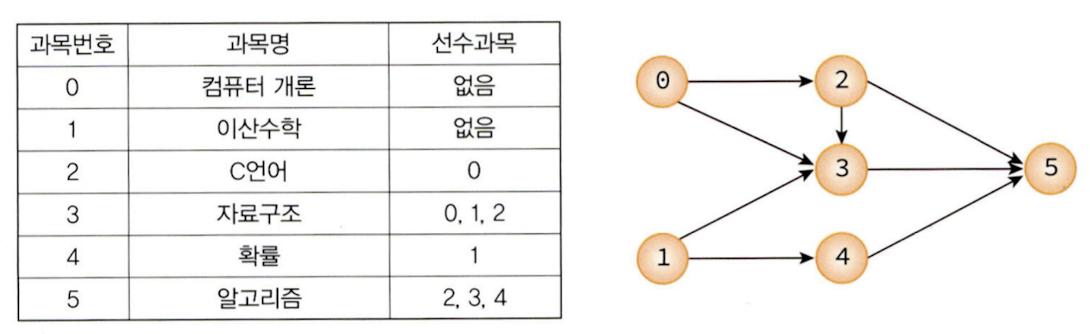
위상 정렬은 방향성이 있는 비순환 그래프(DAG)의 정점들을 선형적으로 나열하는 정렬 방법이다.이 정렬은 그래프의 간선 방향에 따라 특정 순서를 유지해야 할 때 유용하다. 예를 들어, 작업 우선순의, 수업 과목의 선수 과목 체계, 컴파일러의 의존성 분석 등을 다룰 때
9.선택 정렬(Selection Sort)
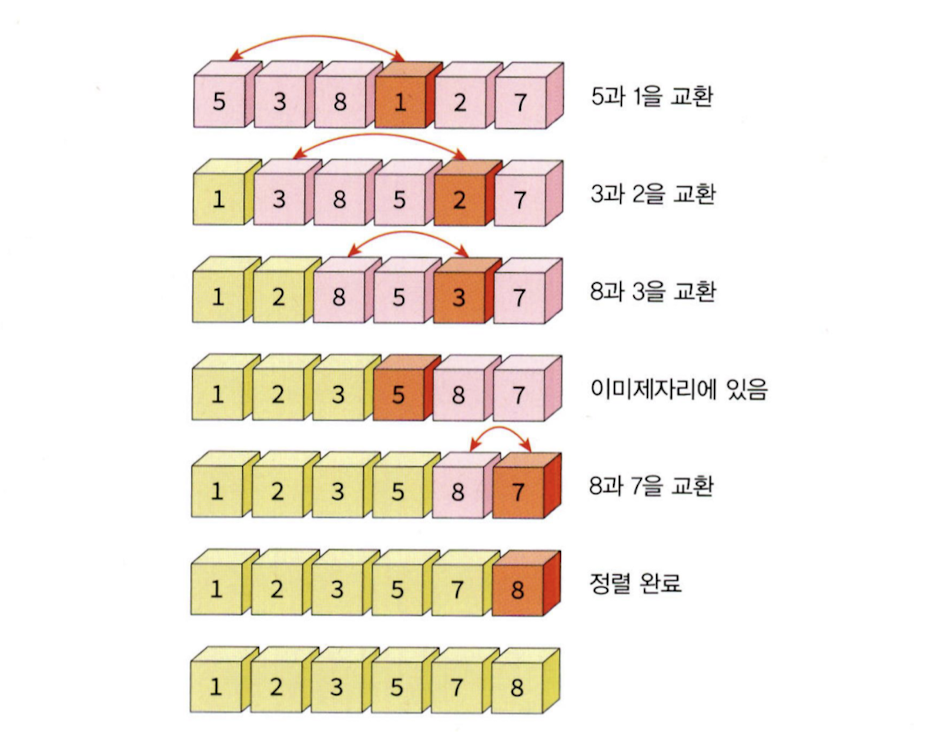
선택 정렬은 간단한 정렬 알고리즘 중 하나로, 배열이나 리스트를 정렬하는 데 사용된다. 동작 과정은 다음과 같다.주어진 리스트에서 최소값(또는 최대값)을 찾는다.찾은 값을 현재 정렬되지 않은 부분의 첫 번째 요소와 교환한다.정렬된 부분을 확장하고, 정렬되지 않은 부분
10.삽입 정렬(Insertion Sort)
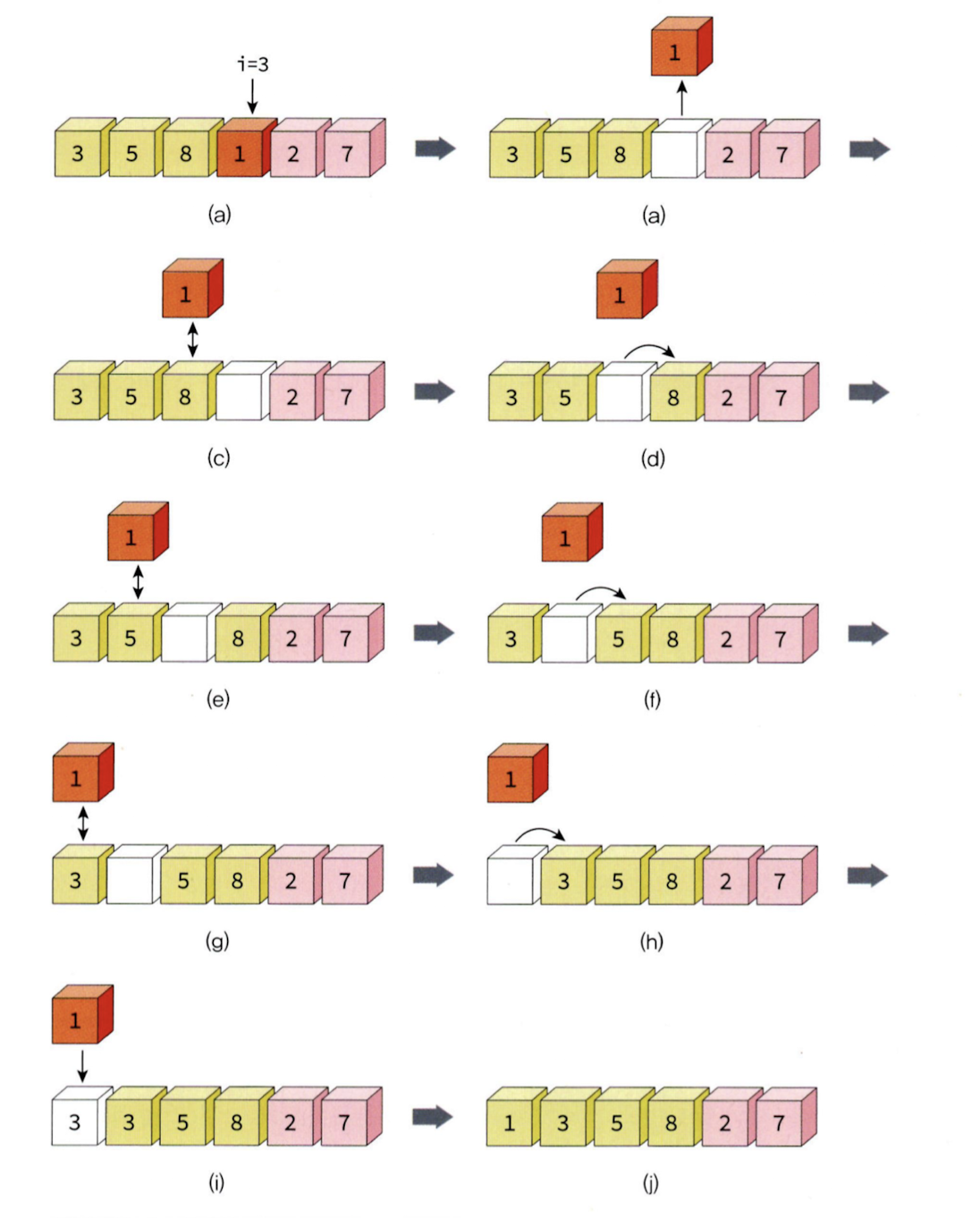
삽입 정렬은 간단하면서도 효율적인 정렬 알고리즘 중 하나로, 주로 데이터 양이 적거나 거의 정렬된 경우에 적합하다. 삽입 정렬은 배열의 요소를 하나씩 순회하며, 현재 요소를 정렬된 부분에 적절한 위치에 삽입하는 방식으로 동작한다.초기 설정: 첫 번째 요소는 이미 정렬된
11.알고리즘 - 쉘 정렬(Shell Sort)

쉘 정렬은 삽입 정렬의 일반화된 형태로, 데이터의 정렬 속도를 높이기 위해 고안된 정렬 알고리즘이다. 삽입 정렬은 데이터가 거의 정렬된 상태에서 빠르게 동작하지만, 데이터가 무작위로 배치된 경우에는 성능이 떨어진다. 쉘 정렬은 이를 개선하기 위해 데이터를 부분적으로 정
12.버블 정렬(Bubble Sort)
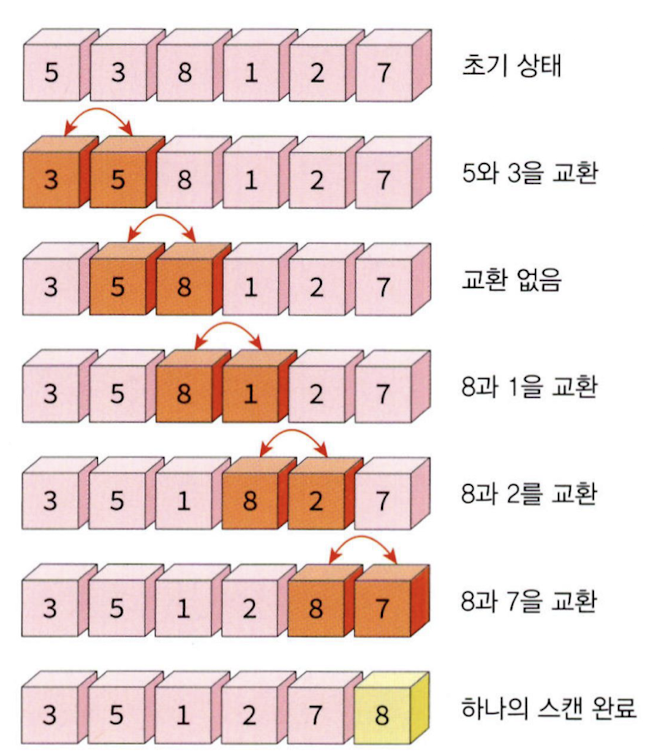
버블 정렬은 정렬 알고리즘 중 가장 기본적인 형태로, 서로 인접한 두 요소를 비교하여 정렬하는 방식이다. 간단하지만, 효율성 측면에서는 다른 정렬 알고리즘에 비해 떨어진다.배열의 처음부터 시작하여 인접한 두 요소를 비교한다.두 요소의 순서가 잘못된 경우, 서로 교환한다
13.합병 정렬(Merge Sort)
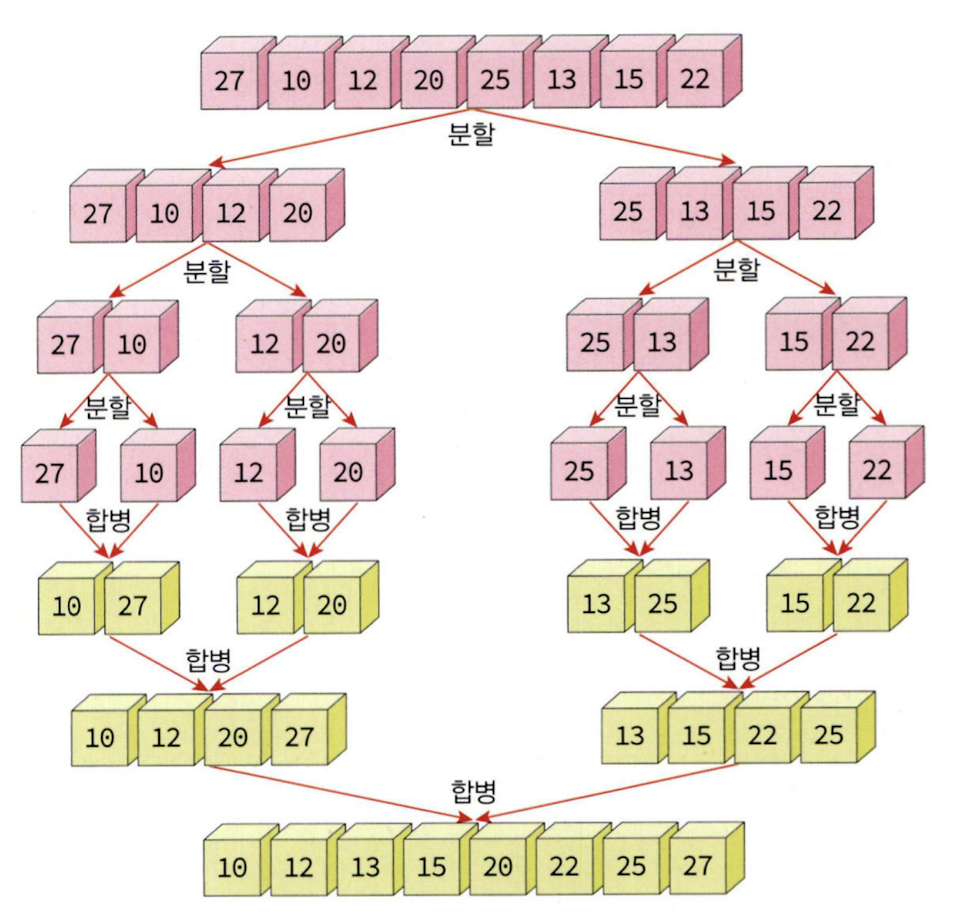
합병 정렬은 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트를 얻고자 하는 것이다. 합병 정렬은 분할 정복 기법에 바탕을 두고 있다. 분할 정복 기법은 문제를 작은 2개의 문
14.퀵 정렬(Quick Sort)
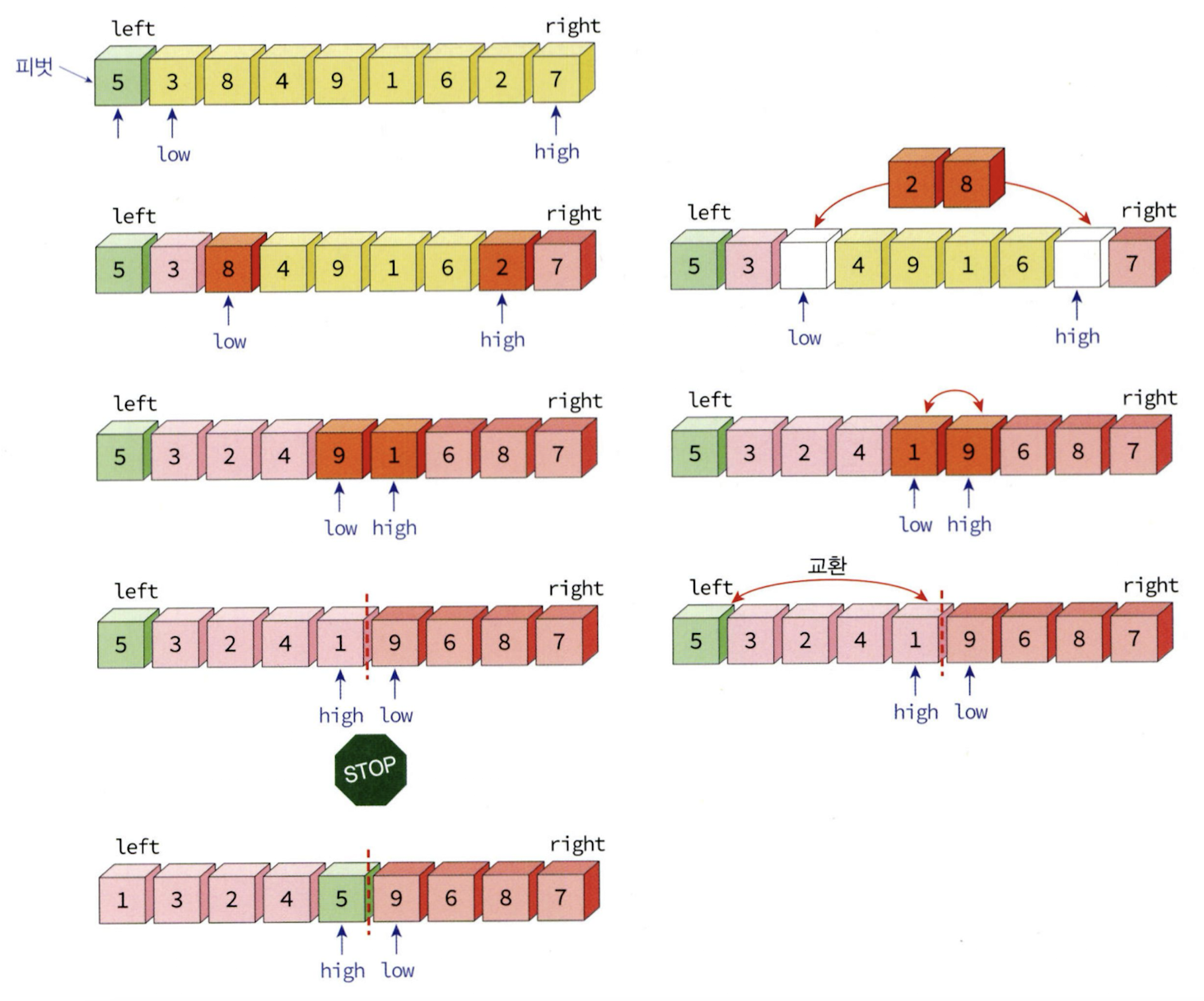
퀵 정렬은 분할 정복 알고리즘의 일종으로, 리스트를 정렬하는 효율적인 방법 중 하나이다. 작동 원리는 다음과 같다.정렬한 리스트에서 하나의 기준 값(피벗)을 선택한다. 피벗은 리스트의 임의의 값일 수 있으며, 일반적으로 처음, 중간, 마지막 값 중 하나로 설정한다.피벗
15.기수 정렬(Radix Sort)
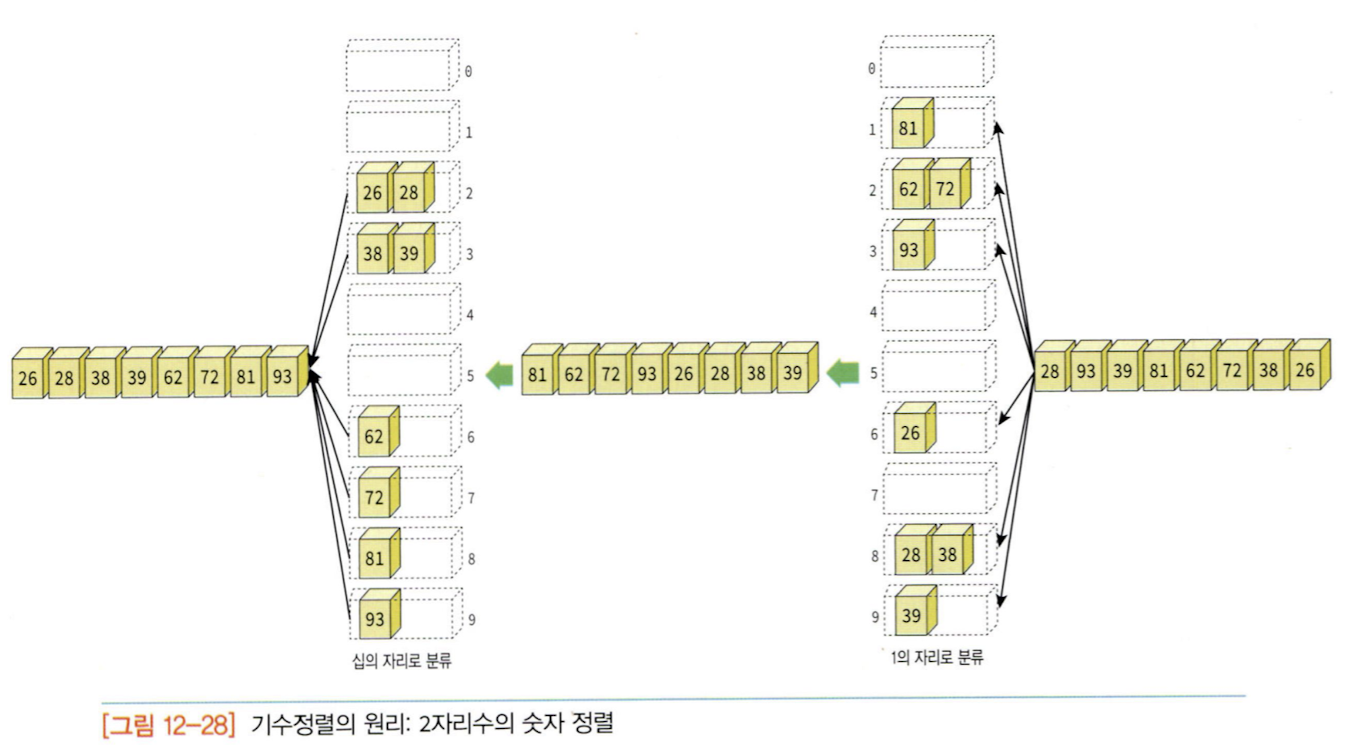
비교 기반 정렬 알고리즘이 아닌 정렬 방식으로, 데이터를 자리수에 따라 처리하여 정렬한다. 주로 정수나 문자열과 같은 데이터를 정렬하는데 사용되며, 안정 정렬(stable sort)에 속한다. 기수 정렬은 데이터를 가장 낮은 자리수(LSD: Least Significa
16.순차 탐색(Sequential Search)
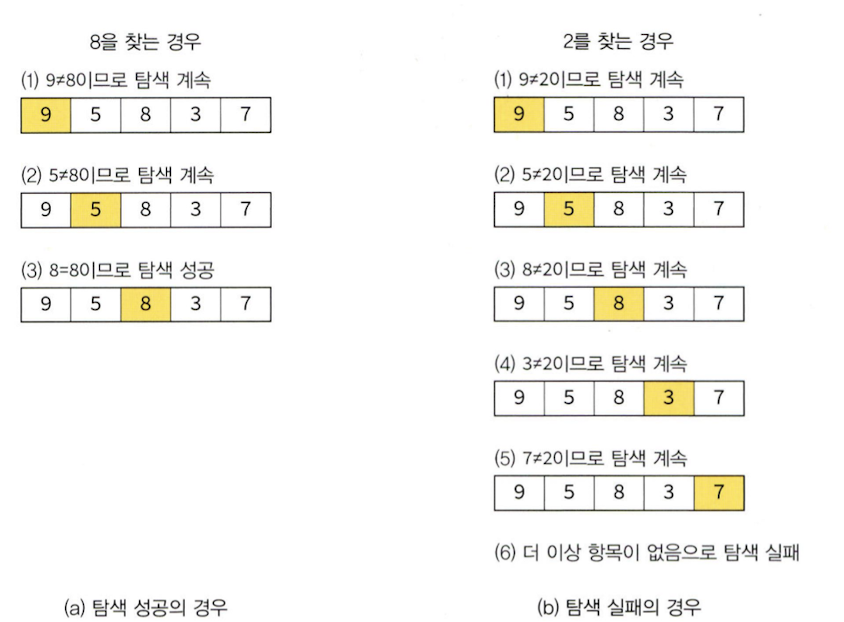
순차 탐색은 탐색 방법 중에서 가장 간단하고 직접적인 탐색 방법이다. 이름에서도 알 수 있다시피 처음부터 끝까지 모두 확인하여 원하는 항목을 찾아가는 방법이다. 코드는 다음과 같다.순차 탐색에서 비교 횟수를 줄이는 방법을 생각해 보자. 위에서 작성된 코드는 리스트 전체
17.이진 탐색(Binary Search)
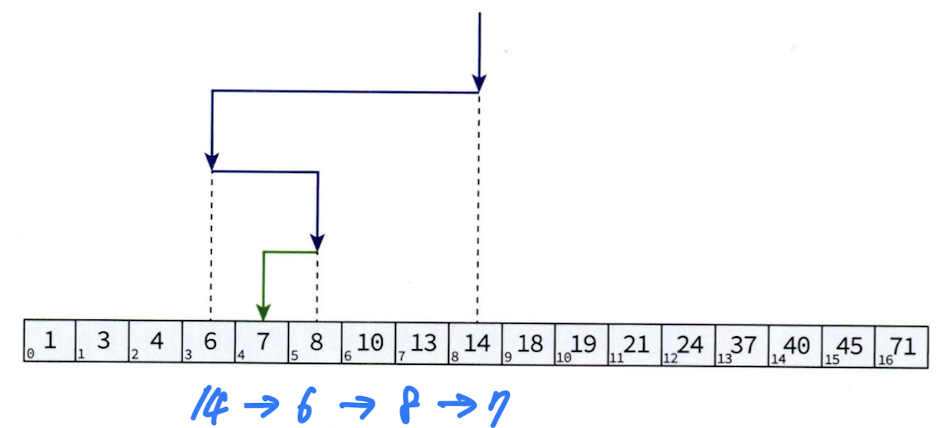
이진 탐색은 정렬된 배열에서 원하는 값을 빠르게 찾는 탐색 알고리즘이다. 이 알고리즘은 탐색 범위를 매 단계마다 절반으로 줄여 효율적으로 값을 얻는다.데이터가 반드시 정렬되어 있어야 한다.데이터의 크기가 클수록 성능 이점이 두드러진다.삽입/삭제가 빈번히 이루어지는 데이
18.색인 순차 탐색(Indexed Sequential Search)
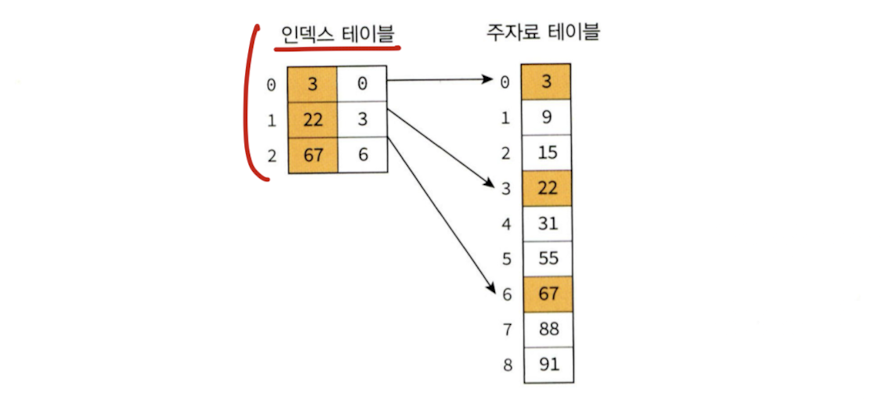
색인 순차 탐색 방법은 순차 탐색과 이진 탐색의 장점을 결합한 탐색으로, 인덱스라 불리는 테이블을 사용하여 탐색의 효율을 높이는 방법이다. 인덱스 테이블은 주 자료 리스트에서 일정 간격으로 발췌한 자료를 가지고 있다. 인덱스 테이블에 m개의 항목이 있고, 주 자료 리스
19.보간 탐색(Interpolation Search)
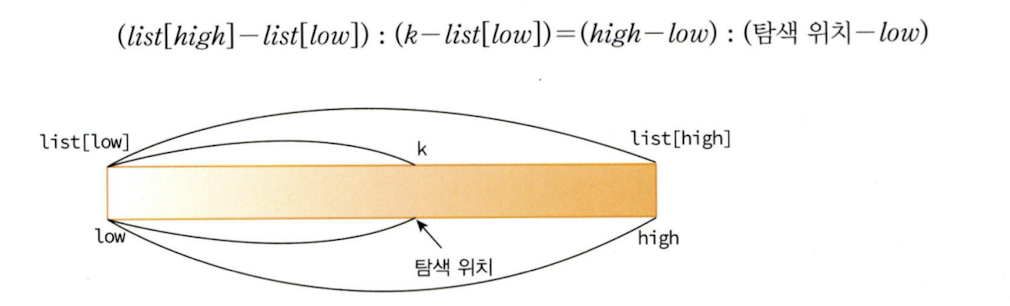
보간 탐색은 정렬된 배열에서 특정 값을 찾기 위한 탐색 알고리즘으로, 탐색키가 존재할 위치를 예측하여 탐색하는 방법이다.보간 탐색은 이진 탐색과 유사하나 리스트를 반으로 분할하지 않고 불균등하게 분할하여 탐색한다. 배열은 항상 정렬되어 있어야 한다.이진 탐색에서 탐색
20.이진 탐색 트리(BST: Binary Search Tree)
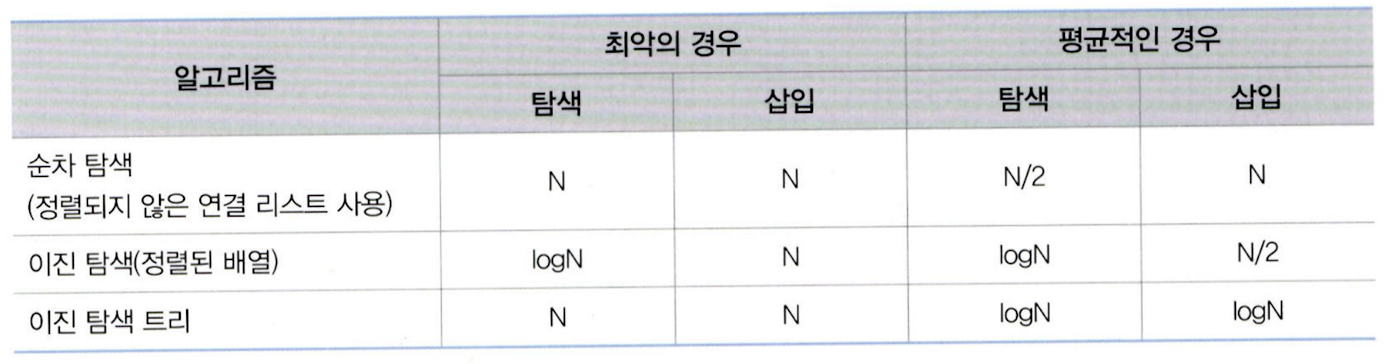
이진 탐색 트리는 근본적으로 이진 탐색과 같은 원리이다. 하지만 이진 탐색은 자료들이 배열에 저장되어 있으므로 삽입과 삭제할 때마다 앞뒤의 원소들을 이동시켜야 하기 때문에 비효율적이다. 반면에 이진 탐색 트리는 비교적 빠른 시간 안에 삽입과 삭제를 끝마칠 수 있는 구조
21.2-3트리
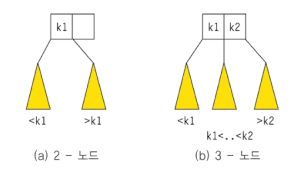
균형 이진 탐색 트리의 일종으로, 각 노드가 2개 또는 3개의 자식을 가질 수 있는 트리 구조이다. 이 트리는 항상 균형을 유지하여 탐색, 삽입, 삭제 등의 연산이 효율적으로 수행되도록 보장한다.2-노드: 이진탐색트리처럼 하나의 데이터 K1와 두 개의 자식 노드를 가진
22.순환과 재귀(Recursion)

재귀적 알고리즘에서 순환은 재귀 호출의 반복적 구조를 의미하며, 이는 문제가 작은 부분 문제로 계속 나뉘고, 그 결과를 결합하여 최종 결과를 도출하는 과정이다.순환은 본질적으로 순환적인 문제가 그러한 자료구조를 다루는 프로그램에 적합하다. 예를 들어 정수의 팩토리얼은
23.알고리즘 - 해싱(Hashing)
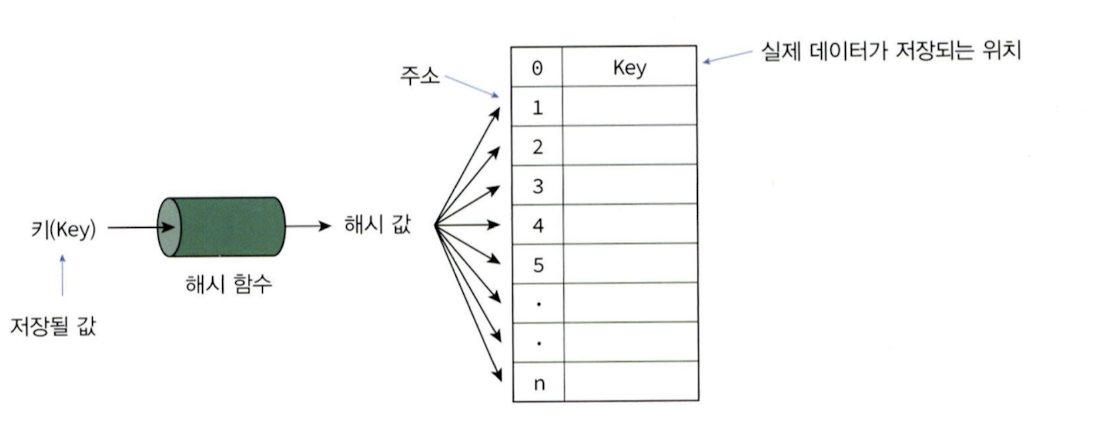
대부분의 탐색 방법들은 키 값 비교로써 탐색하고자 하는 항목에 접근해싱(hashing): 키 값에 대한 산술적 연산에 의해 테이블의 주소를 계산하여 항목에 접근해시 테이블(hash table): 키 값의 연산에 의해 직접 접근이 가능한 구조맵(map) 또는 테이블(ta