색인 순차 탐색(Indexed Sequential Search)

이재원·2024년 12월 31일

알고리즘

목록 보기

18/23

색인 순차 탐색

색인 순차 탐색 방법은 순차 탐색과 이진 탐색의 장점을 결합한 탐색으로, 인덱스라 불리는 테이블을 사용하여 탐색의 효율을 높이는 방법이다. 인덱스 테이블은 주 자료 리스트에서 일정 간격으로 발췌한 자료를 가지고 있다. 인덱스 테이블에 m개의 항목이 있고, 주 자료 리스트의 데이터 수가 n이면 각 인덱스 항목은 주 자료 리스트의 각 n/m번째 데이터를 가지고 있다. 이 때 주 자료 리스트와 인덱스 테이블은 모두 정렬되어 있다.

즉, 색인 순차 탐색은 인덱스 테이블이 주 자료 테이블의 데이터를 바로 접근하여 순차 탐색을 수행하기 때문에, 직접 탐색(Direct Search)과 순차 탐색(Seauential Search)를 합한 것이다.

탐색 과정

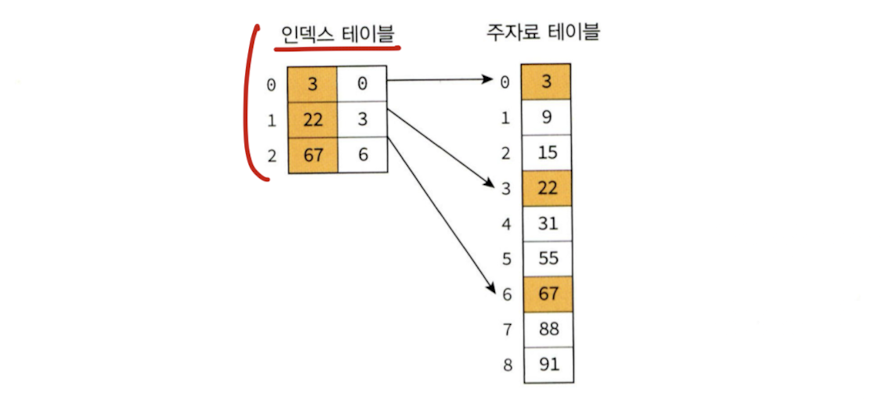
1. 색인(index) 테이블 생성

데이터의 주요 위치(예; 특정 구간의 첫 번째 항목)를 인덱스 테이블로 만들어 저장한다.
인덱스 테이블에는 각 구간의 첫 번째 데이터 값과 해당 데이터의 실제 위치(주소 또는 인덱스)가 포함된다.

2. 인덱스 테이블에서 이진 탐색 수행

탐색하려는 키(Key)가 속할 구간을 찾기 위해 인덱스 테이블에 대해 이진 탐색을 수행한다.
이 과정에서 탐색 키가 속한 데이터 블록의 시작 위치를 확인한다.

3. 해당 구간에서 순차 탐색 수행

색인 테이블에서 찾은 데이터 블록 안에서 순차 탐색을 진행한다.
이로 인해 탐색 범위를 크게 줄일 수 있다.

장점과 단점

장점

탐색 속도 향상: 인덱스 테이블로 탐색 범위를 축소하므로 순차 탐색만 사용하는 경우보다 빠르다.
메모리 절약: 전체 데이터가 아닌 인덱스 테이블만 메모리에 저장하므로 효율적이다.
데이터 추가 및 삭제가 비교적 쉬움: 인덱스 테이블만 업데이트하면 되기 때문에 데이터 조작이 간편하다.

단점

인덱스 테이블 생성 비용: 인덱스 테이블을 생성하고 유지관리해야 하므로 추가적인 메모리가 더 필요하다.
불균형 데이터 문제: 데이터가 고르게 분포하지 않으면 일부 구간에서 순차 탐색의 성능이 저하될 수 있다.
동적 데이터의 효율성 저하: 데이터가 자주 변경되는 경우 색인 테이블의 재구성이 필요하다.

시간 복잡도

색인 순차 탐색의 성능은 인덱스 테이블의 크기에 좌우된다. 인덱스 테이블의 크기를 줄이면 주 자료 리스트에서의 탐색 시간을 증가시키고, 인덱스 테이블의 크기를 크게 하면 인덱스 테이블의 탐색 시간을 증가시킨다.

따라서 인덱스 크기만큼 줄어들기 때문에, 인덱스 테이블의 크기를 m이라 하고 주 자료 리스트의 크기를 n이라 하면 색인 순차 탐색의 복잡도는 $O(m+n/m)$ 와 같다.

적용 사례

데이터베이스 관리 시스템(DBMS): 색인을 사용해 효율적인 데이터 검색을 한다.
파일 시스템: 대량의 파일 검색에서 색인을 활용하여 성능을 개선한다.
검색 엔진: 검색어에 대한 색인을 미리 생성하여 탐색 속도를 높인다.

전체 코드

#include <stdio.h>

#define MAX_SIZE 1000
#define INDEX_SIZE 10

int list[MAX_SIZE] = {3, 9,15, 22, 31, 55, 67, 88, 91};
int n=9;
typedef struct { 
		int key;
		int index; 
} itable;
itable index_list[INDEX_SIZE]={ {3,0}, {15,3}, {67,6} };

int seq_search(int key, int low, int high)
{  
	int i;
    for(i=low; i<=high; i++)
       if(list[i]==key)
	   return i;  /* 탐색에 성공하면 키 값의 인덱스 반환 */
    return -1;    /* 탐색에 실패하면 -1 반환 */
}

/* INDEX_SIZE는 인덱스 테이블의 크기,n은 전체 데이터의 수 */
int index_search(int key)
{  
   int i, low, high;
	/* 키 값이 리스트 범위 내의 값이 아니면 탐색 종료 */
   if(key<list[0] || key>list[n-1])
      return -1;

   /* 인덱스 테이블을 조사하여 해당키의 구간 결정 */
   for(i=0; i<INDEX_SIZE; i++) 
      if(index_list[i].key<=key &&
			 index_list[i+1].key>key)
	 	break;
   if(i==INDEX_SIZE){  /* 인덱스테이블의 끝이면 */
      low = index_list[i-1].index;   
      high = n;
   }
   else{
      low = index_list[i].index;  
      high = index_list[i+1].index;
   }
   /* 예상되는 범위만 순차 탐색 */
   return seq_search(key, low, high);
}

//
void main()
{
		int i;
		i = index_search(67);
		if( i >= 0 ) {
			printf("탐색 성공 i=%d\n", i);
		}
		else {
			printf("탐색 실패\n");
		}
}