합병 정렬

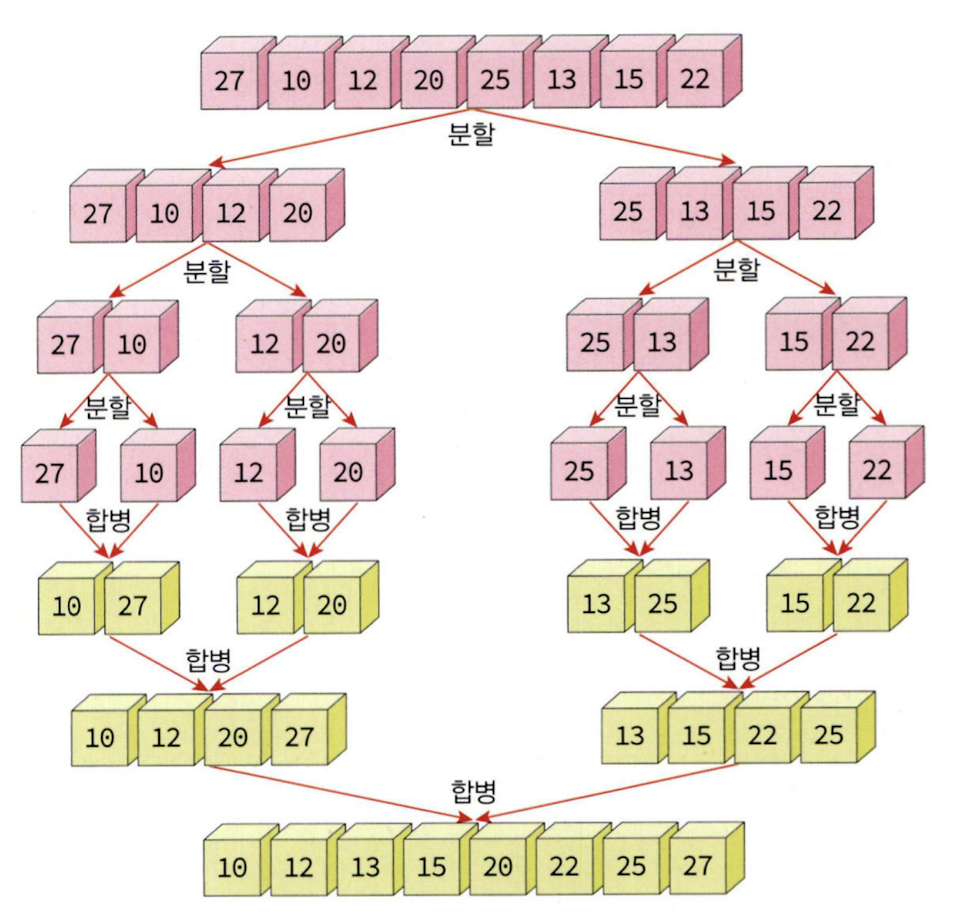
합병 정렬은 하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트를 얻고자 하는 것이다. 합병 정렬은 분할 정복 기법에 바탕을 두고 있다. 분할 정복 기법은 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다. 합병 정렬은 다음의 단계들로 이루어진다.

1. 분할(Divided): 입력 배열을 같은 크기의 2개의 부분 배열로 분할한다.
2. 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 이용하여 다시 분할 정복 기법을 적용한다.
3. 결합(Combine): 정렬을 하면서 결합을 하고, 정렬된 부분 배열들을 하나의 배열에 통합한다.

전체 코드

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define MAX_SIZE 10

int list[MAX_SIZE];
int n;

int sorted[MAX_SIZE];

void merge(int list[], int left, int mid, int right) {
	int i, j, k, l;;
	i = left; j = mid + 1; k = left;

	while (i <= mid && j <= right) {
		if (list[i] <= list[j])
			sorted[k++] = list[i++];
		else
			sorted[k++] = list[j++];
	}
	// i의 인덱스가 mid보다 클 경우 첫 번째 배열은 모두 정렬되었음을 보장함
	if (i > mid)
		for (l = j; l <= right; l++)
			sorted[k++] = list[l];
	else
		for (l = i; l <= mid; l++)
			sorted[k++] = list[l];
	for (l = left; l <= right; l++)
		list[l] = sorted[l];
}

void merge_sort(int list[], int left, int right) {
	int mid;
	if (left < right) {
		mid = (left + right) / 2;
		merge_sort(list, left, mid);
		merge_sort(list, mid + 1, right);
		merge(list, left, mid, right);
	}
}

int main(void) {
	int i;
	n = MAX_SIZE;
	srand(time(NULL));
	for (i = 0; i < n; i++) 
		list[i] = rand() % 100;

	merge_sort(list, 0, n - 1);
	for (i = 0; i < n; i++)
		printf("%d ", list[i]);
	printf("\n");
	return 0;
}

주목할 점은 merge 함수 호출하면 sorted라는 새로운 배열에 데이터를 정렬하며 복사한다는 점이다.

또한 합병 과정에서 i가 mid보다 크면 i는 이미 정렬을 다 했다는 뜻이므로 왼쪽 배열을 모두 채워주는 것 역시 주목할 부분이다.

합병 정렬의 시간 복잡도

합병 정렬은 순환 호출 구조로 되어 있다. 따라서 레코드의 개수 n이 2의 거듭제곱이라고 가정ㅇ하고 순환 호출의 깊이가 얼마나 되는지를 분석해 보자. 만약 $n=2^3$인 경우에는 부분 배열의 크기가 $2^3$ → $2^2$ → 2 → $2^0$ 으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 따라서 일반적으로 $n=2^k$라고 하면 순환 호출의 깊이가 k가 될 것이다. 여기서 $k = log_2n$ 임을 알 수 있다.

그리고 합병 단계에서 최대 n번의 비교 연산이 필요하므로 총 비교 연산은 최대 $nlog_2n$이다. 합병 정렬의 장점 중 하나는 안정적인 정렬 밥법이며 데이터의 분포에 영향을 덜 받는다. 즉, 최악, 평균, 최선의 경우의 시간 복잡도가 모두 $O(nlog_2n)$이다.

출처
C언어로 쉽게 풀어쓴 자료구조 - 천인구