[DX] 직교화 (Orthogonalization)

정의

직교화(Orthogonalization)는 여러 벡터 집합에서 서로 수직(직교)인 벡터 집합을 만드는 과정이다.

두 벡터 u,v가 있다면, 이들 사이의 내적이 0이면 u⊥v라 하며, 이럴 때 두 벡터는 서로 직교한다고 한다.

직교화의 대표적인 목적은 주어진 벡터들로부터 직교기저(orthogonal basis) 혹은 정규직교집합(orthonormal set)을 만드는 것이다.

그람 - 슈미트 과정을 이용한 직교화

• 일차독립 벡터들로부터 직교기저를 만드는 대표적인 방법이다.

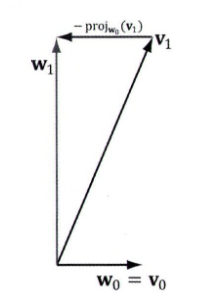
벡터 집합 $\vec{v}_0, \vec{v}_1$에 대해 데카르트 좌표계 (2D 평면) 상에서
1. ${w}_0 = {v}_0$
2. ${w}_1 = {v}_1 - \text{proj}_{u_0}({v}_1)$

으로 표현이 가능하다.

외적을 이용한 직교화

• 벡터 $\vec{v}_1, \vec{v}_2$에서 시작해서 직교 벡터 3개를 만들 수 있다.
  
  

$\vec{v}_1 = (1, 0, 0) , \vec{v}_2 = (1, 1, 0)$으로 두 벡터가 주어져 있다고 가정한다.

1. 첫 번째 벡터는 그대로 사용:

   $u_1 = v_1 = (1, 0, 0)$

2. $v_2$에서 $u_1$ 방향 성분을 제거:

   $\text{proj}_{u_1}(v_2) = \frac{v_2 \cdot u_1}{u_1 \cdot u_1} u_1 = \frac{1}{1}(1, 0, 0) = (1, 0, 0)$
   
   
   $u_2 = v_2 - \text{proj}_{u_1}(v_2) = (1,1,0) - (1,0,0) = (0,1,0)$

   이제 $u_1$과 $u_2$는 서로 직교한다.

3. $u_3$는 $u_1, u_2$의 외적을 이용해 구한다.

   $u_3 = u_1 \times u_2 = (1,0,0) \times (0,1,0) = (0,0,1)$
   
   

이렇게 해서 구해진 직교 벡터 집합은 다음과 같다.