[알고리즘] 브루트포스 (완전 탐색)

leeeha·2022년 7월 1일

알고리즘

목록 보기

11/20

출처: https://github.com/klmyoungyun/Tools-Algorithm

브루트포스

우리말로 완전 탐색이다. 즉, 모든 경우의 수를 탐색해보는 것이다.

반복문을 이용한 완전 탐색
재귀를 이용한 완전 탐색

코테에서는 구현력과 적절한 자료구조를 사용할 수 있는지 테스트용으로 자주 출제된다. 따라서 스스로 문제를 많이 풀어보면서 구현력을 기르는 게 답이다.

이번 포스트에서는 반복문으로 완전 탐색할 때 사용되는 몇가지 테크닉을 소개하려고 한다.

누적 합

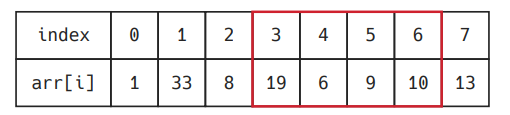
위의 배열에서 인덱스 3부터 6까지에 있는 원소들의 합을 구하려면 어떻게 해야 할까?

일반적으로, 반복문을 이용해서 구할 수 있다.

int answer = 0;
for(int i = 3; i <= 6; i++) answer += arr[i];

이 방법은 구간의 크기에 비례하여 연산 시간이 늘어나므로, 시간복잡도가 O(n)이다. 이것을 O(1)로 줄일 수 있는 방법을 알아보자!

먼저 간단하게 설명하자면, 인덱스 3~6까지의 원소들의 합을 구하려면 0~6까지의 원소들의 합에서 0~2까지의 합을 빼면 된다! 즉, 누적 합에서 누적 합을 빼면 되는 것이다!

이 방법은 0에서 i번째까지의 누적 합을 저장하는 배열이 있다면, 특정 구간의 원소의 합을 구간 크기와 관계없이 항상 일정한 시간 내에 구할 수 있게 해준다. 즉, 시간복잡도가 O(1)로 줄어든 것이다!

아래 예시를 한번 살펴보자! psum[i]은 인덱스 0부터 i번째까지의 합을 저장하는 배열이다.

여기서 인덱스 3부터 6까지의 합은 psum[6] - psum[2]로 구할 수 있다! 누적 합에서 누적 합을 빼는 원리! 이를 코드로 작성하면 어떻게 될까?

// 인덱스 i부터 j까지의 구간 합 구하기 (i <= j) 
int partial_sum(int* psum, int i, int j){
	if(i == 0) return psum[j]; // 예외 처리 
    return psum[j] - psum[i - 1]; // j까지의 누적 합에서 (i-1)까지의 누적 합 빼기 
}

투 포인터

투 포인터란, 두 개의 포인터(커서)를 움직이면서 O(n)에 배열을 탐색하는 방법이다. 여기서 포인터는 단순히 배열의 인덱스를 가리키는 변수라고 보면 된다.

위처럼 오름차순으로 정렬된 배열에서 $a_i + a_j= 13$ (0 <= i <= j <= 8)을 만족하는 ( $a_i, a_j$ ) 쌍의 개수를 구해보자.

이 문제를 일반적인 완전 탐색으로 풀면 다음과 같고, 시간복잡도가 O( $n^2$ )이다. 하지만, 여기서 투 포인터 방법으로 불필요한 연산을 생략한다면, 시간복잡도를 O(n)으로 줄일 수 있다!

int answer = 0;
for(int i = 0; i < 9; i++) {
	for(int j = i + 1; j < 9; j++) {
    	if(a[i] + a[j] == 13) answer++; 
    }
}

그렇다면, 불필요한 연산이 뭘까? 일단, 완전 탐색을 진행해보자!

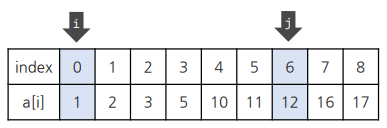
i = 0, j = 6일 때 두 원소의 합이 13이므로 answer 값을 증가시킨다.

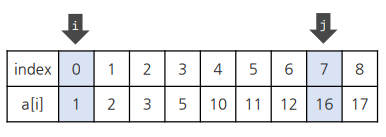
이후 j 값이 증가하면 a[0] + a[7] > 13이 되는데, 여기서 불필요한 연산을 찾을 수 있다! 현재 배열은 오름차순으로 정렬되어 있으므로, a[0] + a[7] > 13이라면 a[0] + a[8]은 계산을 해보지 않아도 13보다 크다는 걸 예상할 수 있다. 따라서 a[i] + a[j] > 13이면 j를 증가시킬 필요가 없다!

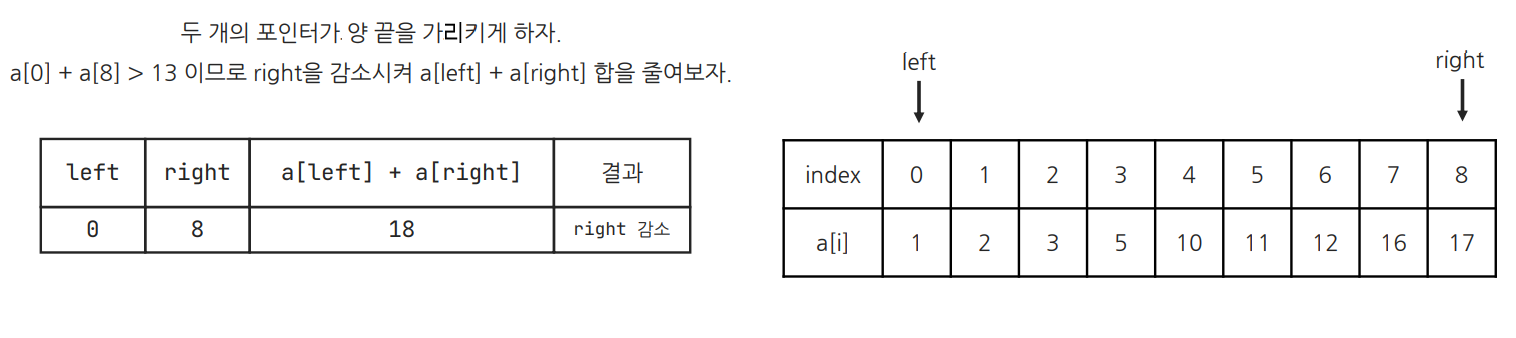
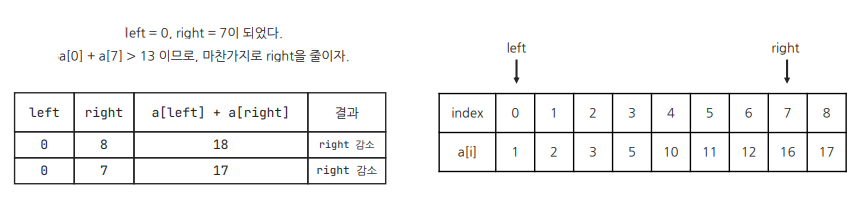
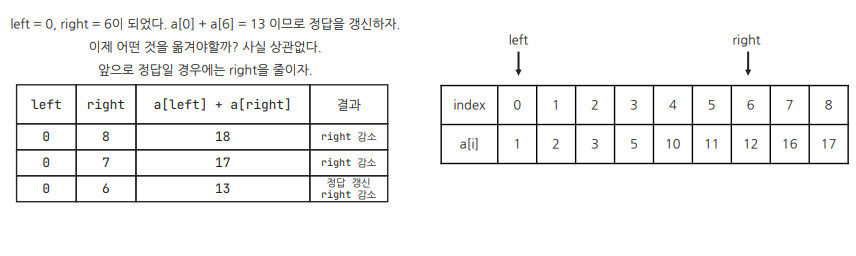
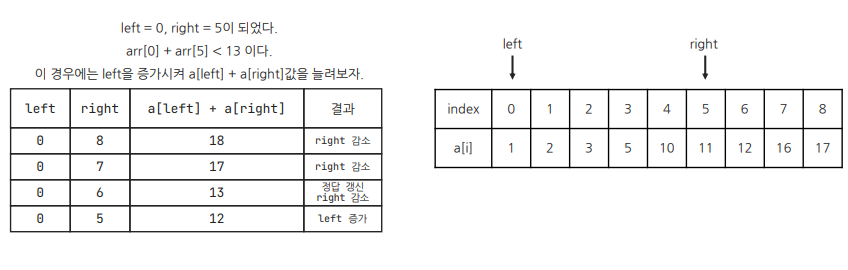
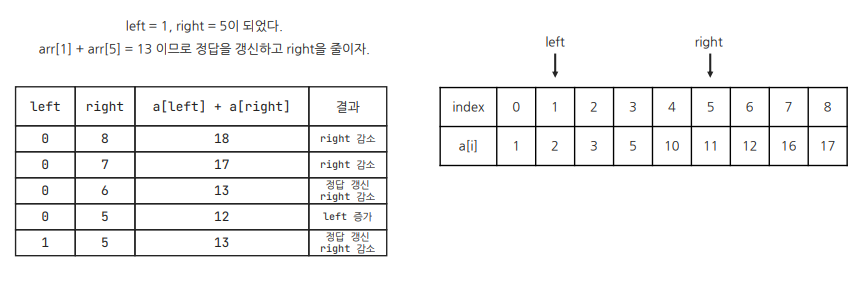
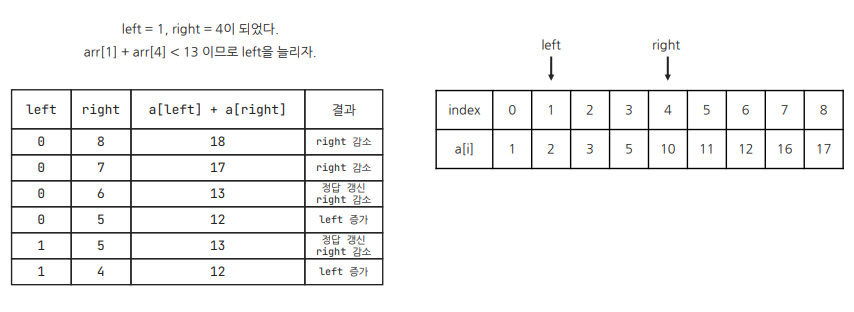
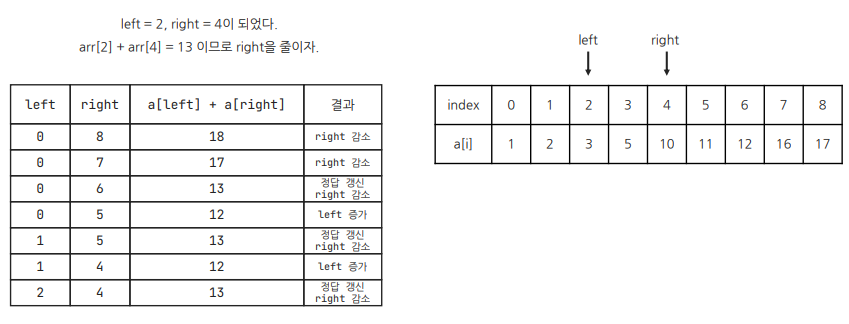
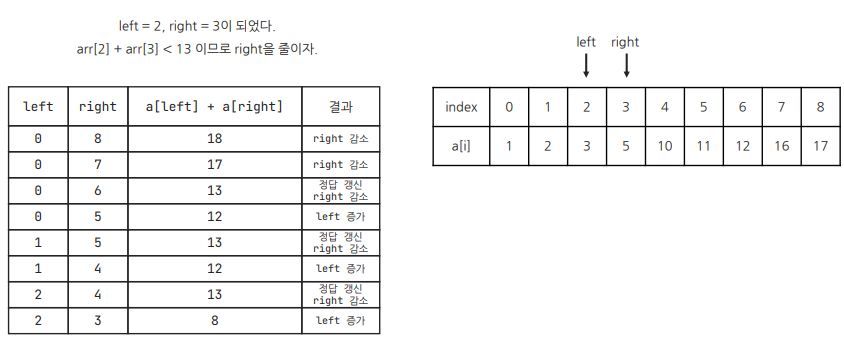
cf) 오타 정정: arr[2] + arr[3] < 13이므로 left를 늘린다.

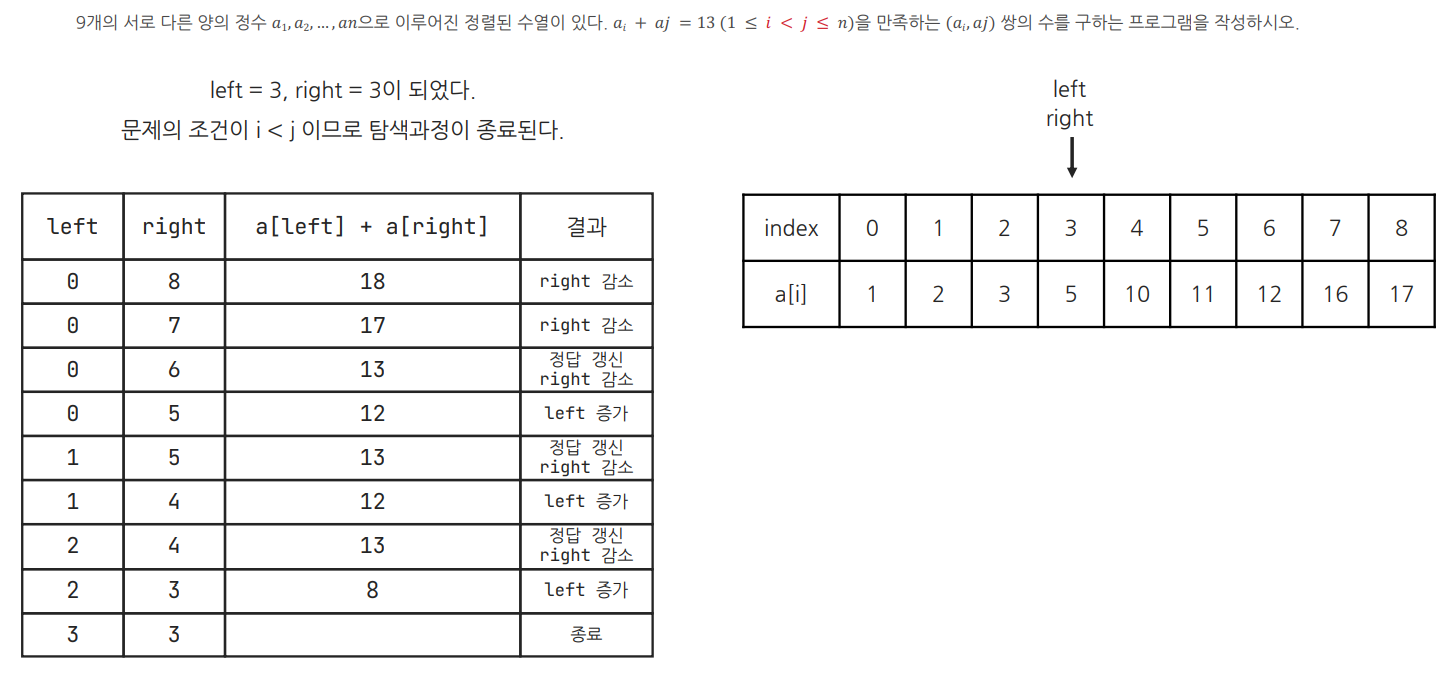
left와 right가 양쪽에서 다가오는데 중간에 만나면 탐색이 멈추므로, left와 right가 움직인 거리는 총 배열의 길이와 같다. 따라서 시간복잡도는 O(n)이다!

// a는 오름차순으로 정렬된 배열이어야 함. 
int left = 0, right = n - 1, answer = 0;
while(left < right){
	if(a[left] + a[right] > 13) right--;
    else if(a[left] + a[right] < 13) left++;
    else { answer++; right--; }
}

위처럼 left, right가 서로 다른 쪽에서 다가오는 경우뿐만 아니라 left, right가 같은 쪽에서 시작하는 경우도 있다고 한다.

슬라이딩 윈도우

위와 같은 배열에서 연속된 3개의 원소의 합 중에서 최댓값을 구하려면 어떻게 해야 할까? 완전 탐색으로 풀면 다음과 같고, 시간복잡도는 O(nm)이다.

int answer = 0;
for(int i = 0; i <= n - m; i++){
	int sum = 0; 
    for(int j = 0; j < m; j++) sum += a[i + j];
    answer = max(answer, sum); 
}

이 문제를 슬라이딩 윈도우 방법으로 풀면 시간복잡도를 O(n)으로 줄일 수 있다!

윈도우 크기를 정한다.

첫번째 윈도우에서 값을 계산한다.

첫번째 계산 값을 기반으로 윈도우를 옮겨가며, 값을 갱신한다.

간단히 말하면, 윈도우의 가장 왼쪽 원소는 슬라이스 하듯이 자르고, 오른쪽에는 새로운 원소를 추가하는 식으로 배열 전체를 순회하기 때문에 시간복잡도가 O(n)으로 줄어든다.

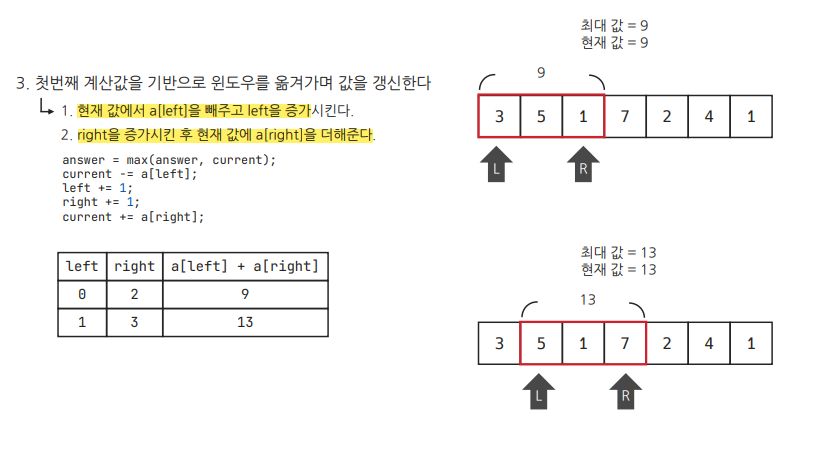
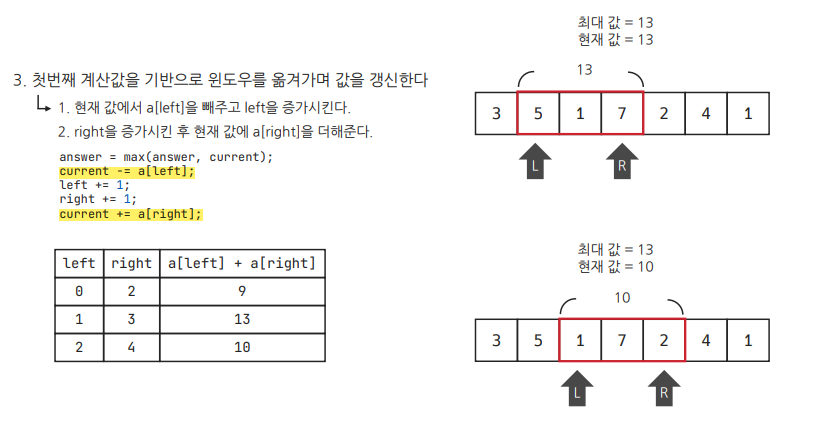
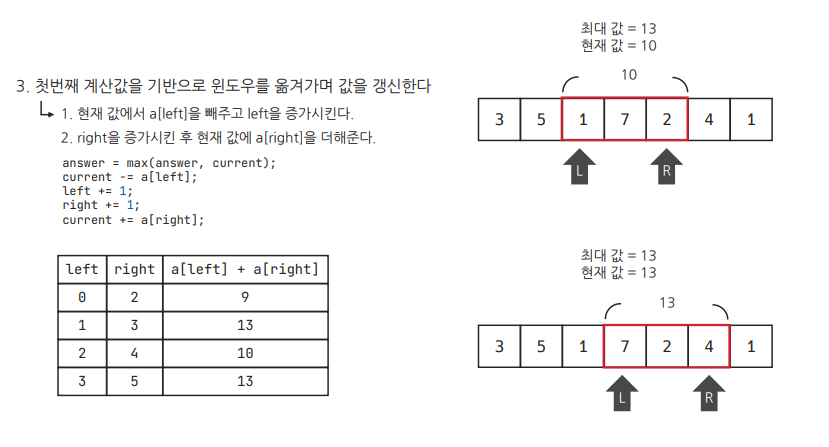
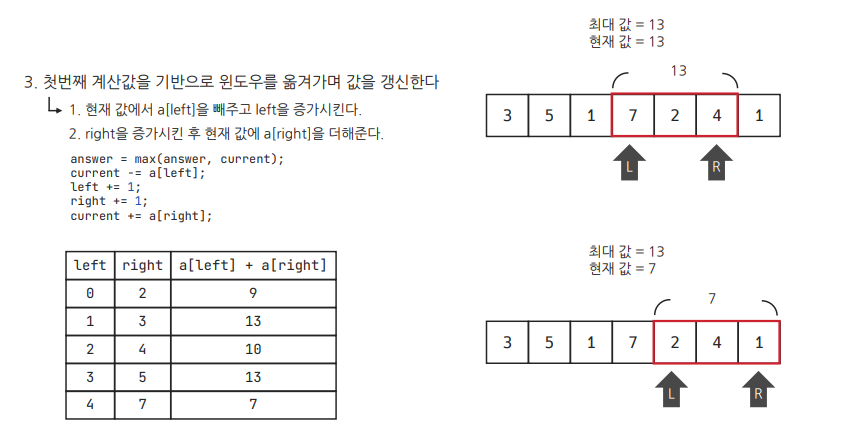
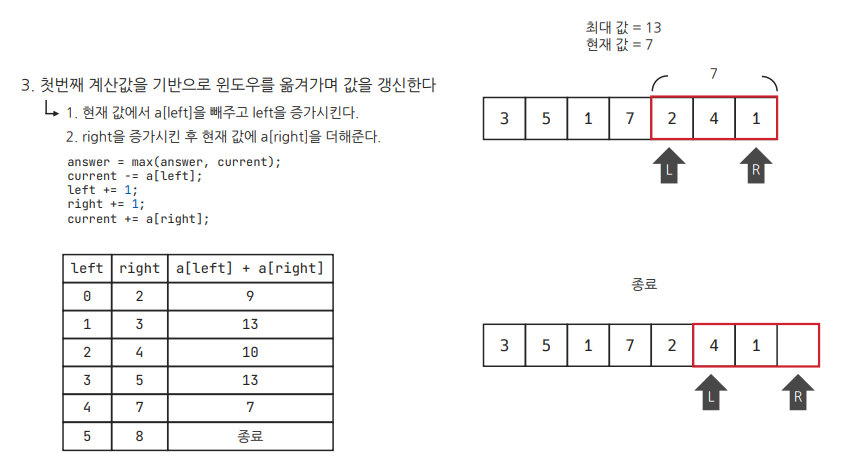
원소의 개수가 n개인 배열에서 윈도우 크기가 m일 때, right가 m-1번째 인덱스부터 n번째 인덱스까지 움직인다. 따라서 시간복잡도는 O(n-m)인데, 보통 n > m이므로 O(n)이라고 부르기도 한다.

int left = 0, sum = 0;
int ans = -1e9; // 더해서 음수가 되는 경우도 있으니까, 초기값 유의하기 

for(int right = 0; right < n; right++){ 
	sum += v[right]; // 오른쪽에 추가 
    
	if(right >= m - 1){ 
		ans = max(ans, sum); 
		sum -= v[left++]; // 왼쪽 슬라이딩  
	} 
}

[알고리즘] 브루트포스 (완전 탐색)

알고리즘

브루트포스

누적 합

관련 문제

투 포인터

관련 문제

슬라이딩 윈도우

관련 문제

[알고리즘] DFS/BFS

[알고리즘] 백트래킹 (Back-tracking)

0개의 댓글