참고 자료
https://youtu.be/1vLqC1rItM8
https://gyoogle.dev/blog/algorithm/DFS%20&%20BFS.html

---

그래프 탐색 알고리즘

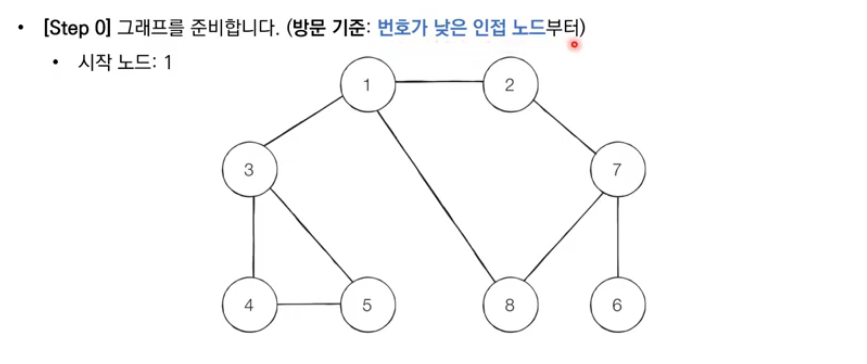
탐색(Search)이란, 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정이다. 대표적인 그래프 탐색 알고리즘으로는 DFS와 BFS가 있다. DFS와 BFS는 코딩 테스트에서 매우 자주 등장하는 유형이므로 반드시 숙지해야 한다. (DFS와 BFS 알고리즘을 공부하기 전에 알아야 하는 기본적인 개념들은 아래 링크를 참고하길 바란다.)

https://velog.io/@jxlhe46/자료구조-스택-Stack
https://velog.io/@jxlhe46/자료구조-큐-Queue
https://velog.io/@jxlhe46/알고리즘-재귀-함수

---

DFS (Depth-First Search)

• DFS는 깊이 우선 탐색이라고도 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
• 루트 노드 혹은 임의 노드에서 다음 브랜치로 넘어가기 전에 해당 브랜치를 모두 탐색하는 방법이다. 따라서 모든 노드를 방문해야 하는 경우에 적합하다.
• DFS는 스택 자료구조 (혹은 재귀함수)를 이용하며, 구체적인 동작 과정은 다음과 같다.

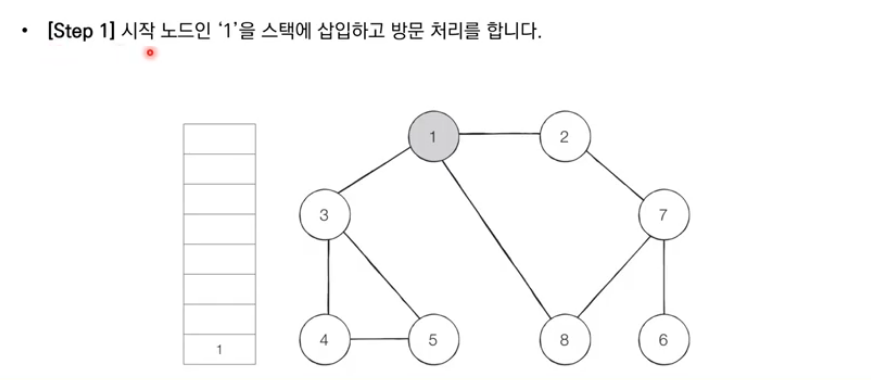
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리한다.
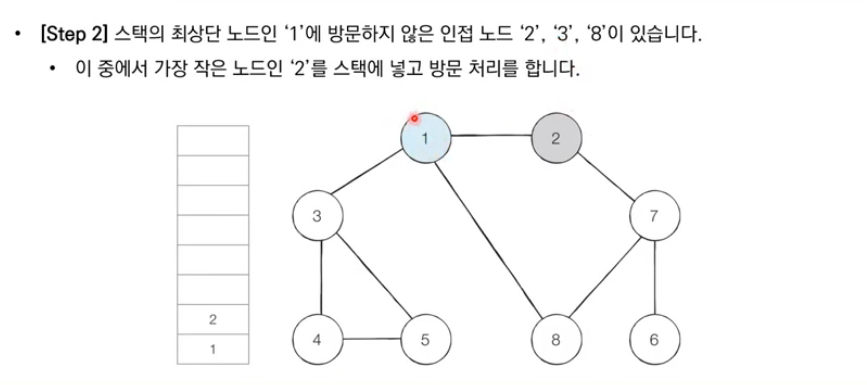
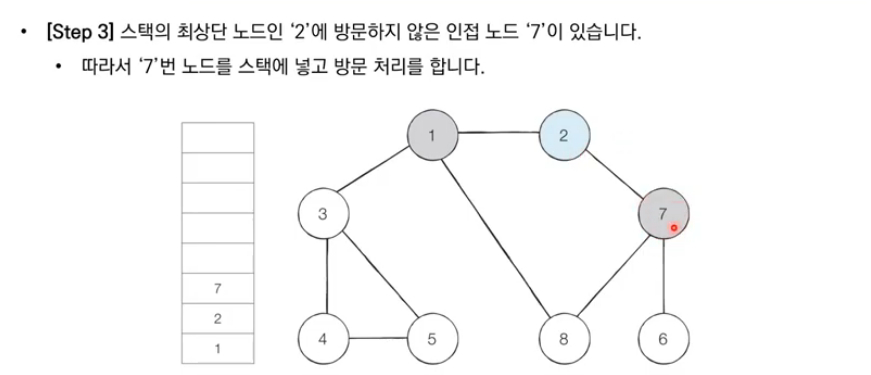
2. 스택의 최상단 노드에 방문하지 않은 인접 노드가 하나라도 있으면, 그 노드를 스택에 넣고 방문 처리한다. 방문하지 않은 인접 노드가 없으면, 스택에서 최상단 노드를 꺼낸다.
3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.

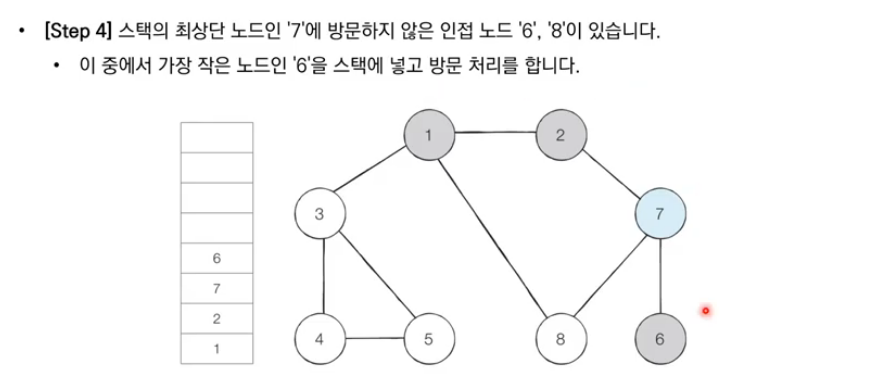
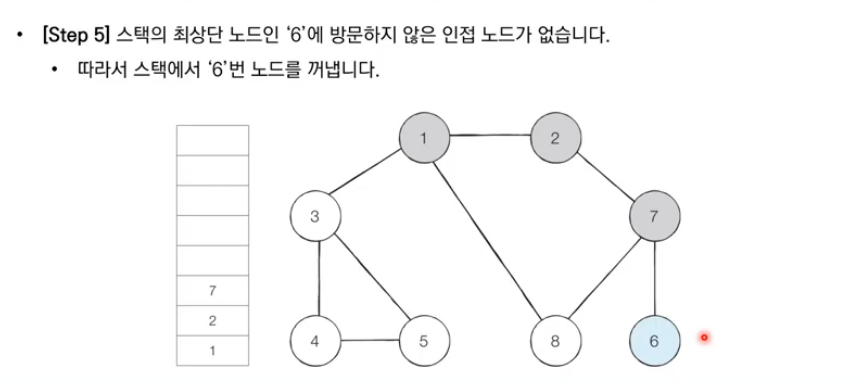
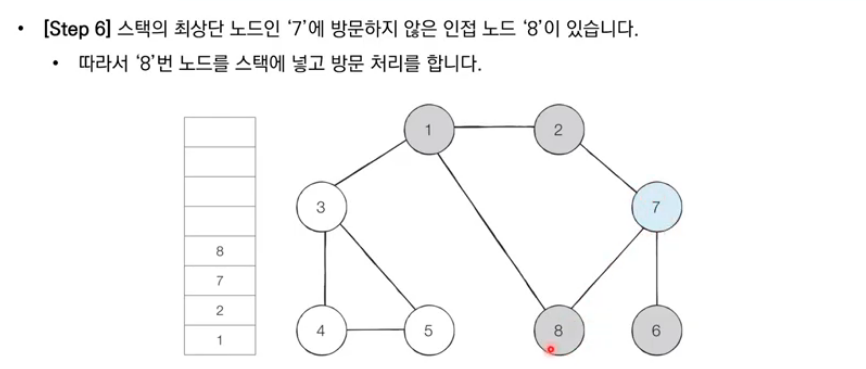
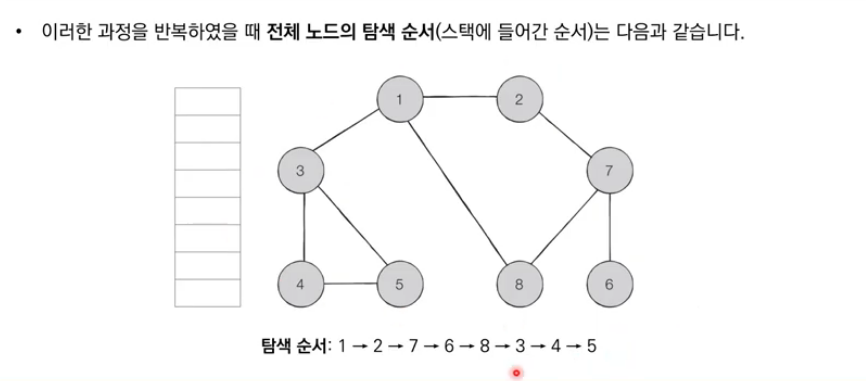
이처럼 재귀적으로 방문하지 않은 노드들을 계속해서 방문하면, 깊이 우선으로 최대한 깊게 그래프를 탐색할 수 있다.

C++ 코드

#include <iostream>
#include <vector>
using namespace std;

bool visited[9]; // 전역으로 선언하면 모두 false로 초기화 됨. 
vector<int> graph[9]; // 벡터 자체가 9개 

void dfs(int x) {
	// 현재 노드 방문 처리
	visited[x] = true;
	cout << x << ' ';

	// 그와 연결된 방문하지 않은 노드를 발견할 때마다 재귀호출 
	for (int i = 0; i < graph[x].size(); i++) {
		int y = graph[x][i]; 
		if (!visited[y]) dfs(y);
	}
}

int main(void) {
	// 노드 1에 연결된 노드 정보 저장 
	graph[1].push_back(2);
	graph[1].push_back(3);
	graph[1].push_back(8);

	// 노드 2에 연결된 노드 정보 저장 
	graph[2].push_back(1);
	graph[2].push_back(7);

	// 노드 3에 연결된 노드 정보 저장 
	graph[3].push_back(1);
	graph[3].push_back(4);
	graph[3].push_back(5);

	// 노드 4에 연결된 노드 정보 저장 
	graph[4].push_back(3);
	graph[4].push_back(5);

	// 노드 5에 연결된 노드 정보 저장 
	graph[5].push_back(3);
	graph[5].push_back(4);

	// 노드 6에 연결된 노드 정보 저장 
	graph[6].push_back(7);

	// 노드 7에 연결된 노드 정보 저장 
	graph[7].push_back(2);
	graph[7].push_back(6);
	graph[7].push_back(8);

	// 노드 8에 연결된 노드 정보 저장 
	graph[8].push_back(1);
	graph[8].push_back(7);

	dfs(1);
}

실행 결과: 1 2 7 6 8 3 4 5

---

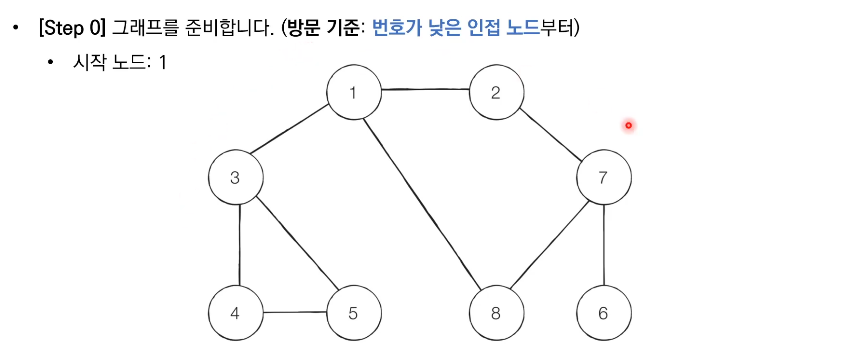
BFS (Breadth-First Search)

• BFS는 너비 우선 탐색이라고도 부르며, 그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘이다.
• 모든 노드를 탐색하는 것보다 최소 비용이 우선일 때 적합하다.
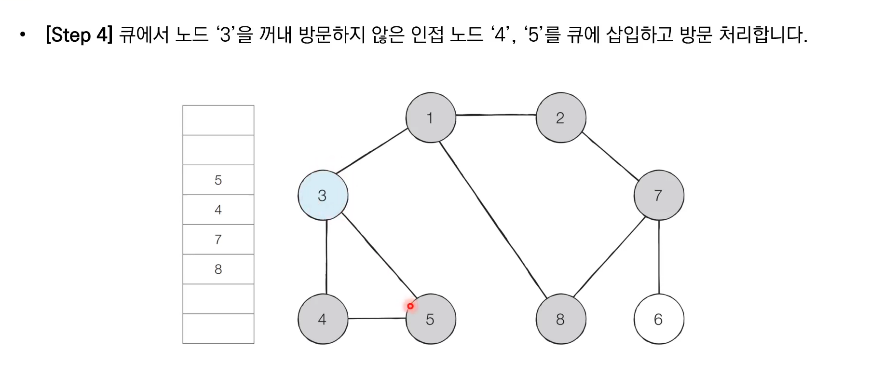
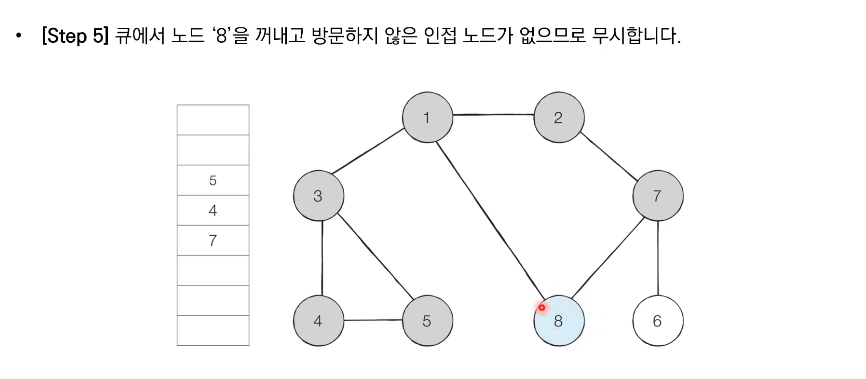
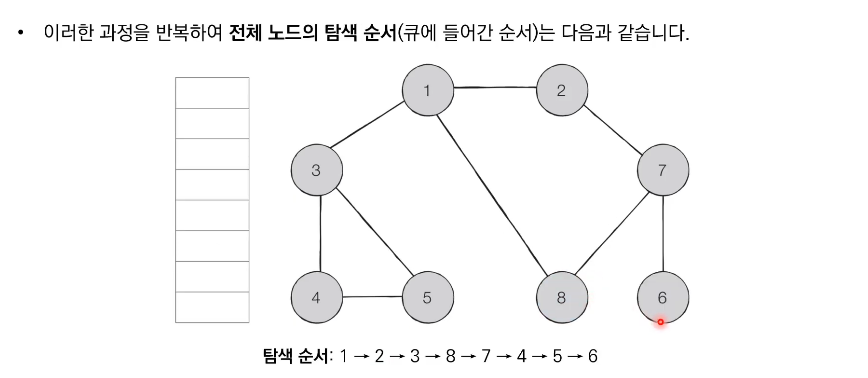
• BFS는 큐 자료구조를 이용하며, 구체적인 동작 과정은 다음과 같다.

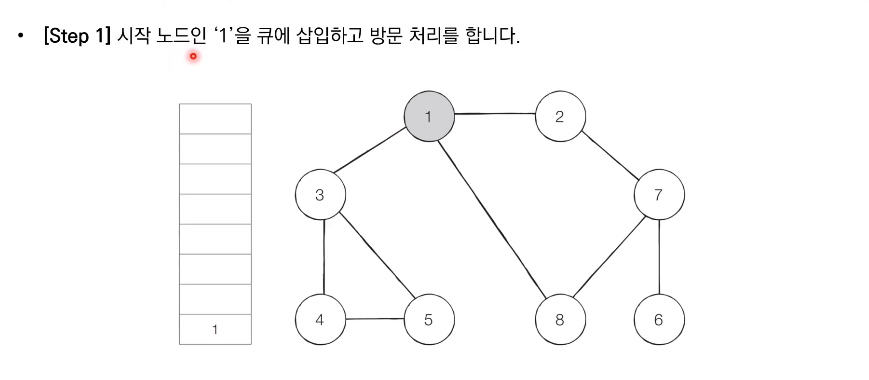
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리한다.
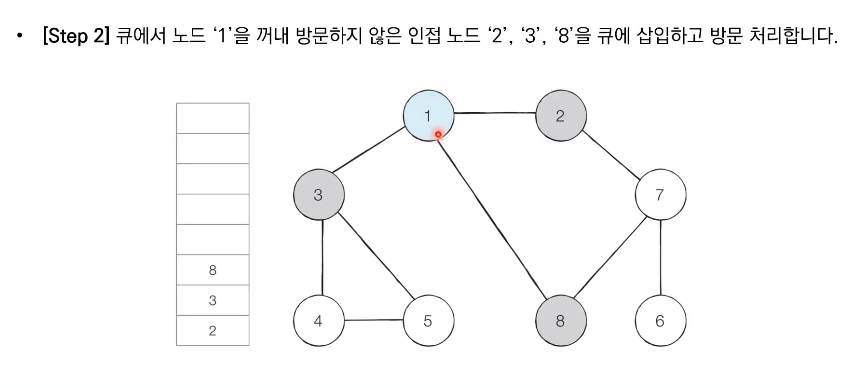
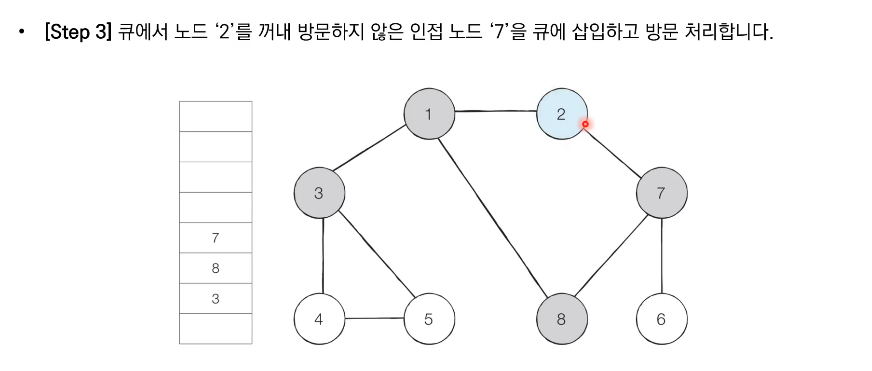
2. 큐에서 노드를 꺼낸 뒤에 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 '모두' 큐에 삽입하고 방문 처리한다.
3. 더 이상 2번의 과정을 수행할 수 없을 때까지 반복한다.

C++ 코드

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

bool visited[9];
vector<int> graph[9];

void bfs(int start) {
	queue<int> q;

	// 현재 노드 방문 처리
	q.push(start);
	visited[start] = true;

	while(!q.empty()) {
		// 큐의 앞에서부터 원소를 하나씩 뽑아서 
		int x = q.front();
		q.pop();
		cout << x << ' ';

		// 그와 연결된 아직 방문하지 않은 노드들 모두 큐에 삽입 
		for(int i = 0; i < graph[x].size(); i++) {
			int y = graph[x][i];
			if(!visited[y]) {
				q.push(y);
				visited[y] = true;
			}
		}
	}
}

int main(void) {
	// 노드 1에 연결된 노드 정보 저장 
	graph[1].push_back(2);
	graph[1].push_back(3);
	graph[1].push_back(8);

	// 노드 2에 연결된 노드 정보 저장 
	graph[2].push_back(1);
	graph[2].push_back(7);

	// 노드 3에 연결된 노드 정보 저장 
	graph[3].push_back(1);
	graph[3].push_back(4);
	graph[3].push_back(5);

	// 노드 4에 연결된 노드 정보 저장 
	graph[4].push_back(3);
	graph[4].push_back(5);

	// 노드 5에 연결된 노드 정보 저장 
	graph[5].push_back(3);
	graph[5].push_back(4);

	// 노드 6에 연결된 노드 정보 저장 
	graph[6].push_back(7);

	// 노드 7에 연결된 노드 정보 저장 
	graph[7].push_back(2);
	graph[7].push_back(6);
	graph[7].push_back(8);

	// 노드 8에 연결된 노드 정보 저장 
	graph[8].push_back(1);
	graph[8].push_back(7);

	bfs(1);
}

실행 결과: 1 2 3 8 7 4 5 6

---

백준 1260번

https://www.acmicpc.net/problem/1260

문제

그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.

입력

첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.

출력

첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.

C++ 코드

#include <iostream> 
#include <vector> 
#include <string>
#include <algorithm> 
#include <queue> 
#include <cstring> 
using namespace std;

const int MAX = 1001; 
vector<int> graph[MAX]; // 0으로 초기화
bool visited[MAX]; // false로 초기화 

void dfs(int x){
	// 방문한 노드 출력 
	visited[x] = true; 
	cout << x << " "; 

	// 인접한 노드 중에 방문하지 않은 노드가 있으면 재귀 호출 
	for(int i = 0; i < graph[x].size(); i++){
		int y = graph[x][i]; 
		if(!visited[y]) dfs(y); 
	}
}

void bfs(int start){
	queue<int> q;  
	q.push(start); 
	visited[start] = true; 

	while(!q.empty()){ 
    	// 방문한 노드 출력 
		int x = q.front(); 
		q.pop(); 
		cout << x << " "; 

		// 인접한 노드 중에 방문하지 않은 노드 모두 큐에 삽입 
		for(int i = 0; i < graph[x].size(); i++){
			int y = graph[x][i]; 
			if(!visited[y]){ 
				q.push(y); 
				visited[y] = true; 
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	int n, m, v;
	cin >> n >> m >> v; 

	for(int i = 0; i < m; i++){
		int x, y; 
		cin >> x >> y; 
        
        // 양방향 연결 
		graph[x].push_back(y); 
		graph[y].push_back(x); 
	}

	// 각 정점에 연결된 정점 번호들을 오름차순 정렬한다. 
	for(int i = 1; i <= n; i++){ 
		sort(graph[i].begin(), graph[i].end()); 
	}

	dfs(v); 
	
	cout << endl; 
	memset(visited, 0, n + 1); // 1부터 시작하므로 n+1개 초기화 

	bfs(v); 

	return 0;
}