정의와 성질
우선순위가 가장 높은 원소부터 pop 하는 자료구조
- 원소의 추가: O(logN)
- 우선순위가 가장 높은 원소 확인: O(1)
- 우선순위가 가장 높은 원소 제거: O(logN)
위의 연산을 배열로 구현하면, 각각 O(1), O(N), O(N)의 시간복잡도가 걸릴 것이다. 그런데 힙 자료구조를 이용하면 세 연산을 O(logN), O(1), O(logN)에 처리할 수 있다.
기능과 구현
힙은 이진 트리 모양을 갖고 있다. 이진 트리는 각 정점의 자식이 최대 2개인 트리를 의미하고, 힙은 이진 검색 트리와는 다르다. 둘은 이진 트리라는 공통점만 있을 뿐이고 다른 자료구조라는 걸 기억하자.
힙은 최댓값 또는 최솟값을 찾는 목적으로 사용할 수 있고, 최댓값을 찾기 위해 사용하는 힙을 최대 힙, 최솟값을 찾기 위해 사용하는 힙을 최소 힙이라고 한다.
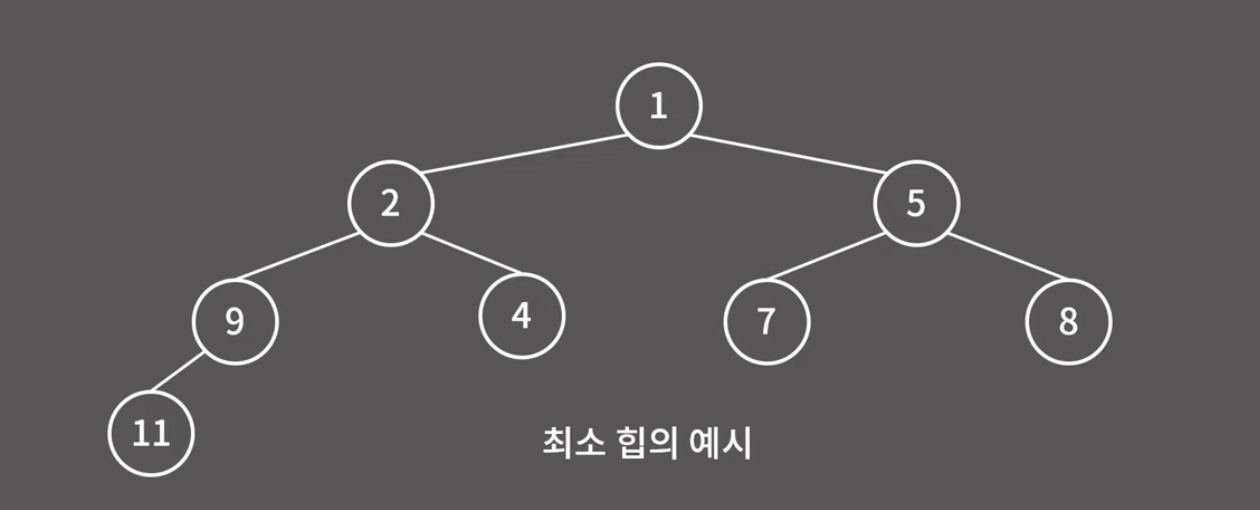
최소 힙에서는 부모가 자식보다 작아야 하고, 최대 힙에서는 부모가 자식보다 커야 한다. 그러면 자연스럽게 최소 힙에서는 루트 노드가 최솟값, 최대 힙에서는 루트 노드가 최댓값이 된다. 이진 검색 트리와 다르게 힙은 불균형이 발생하지 않고 늘 균형이 잘 맞는 이진 트리가 된다.
insert
최소 힙에서 원소를 삽입하는 과정을 살펴보자.

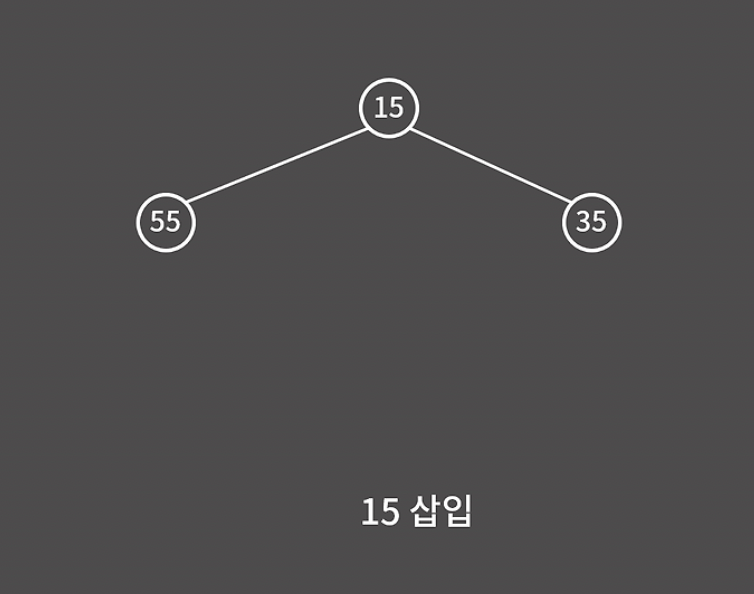
15를 이진 트리에 그냥 삽입하면 최소 힙의 조건에 위배된다. 따라서, 루트 노드와 자리를 바꿔줘야 한다.
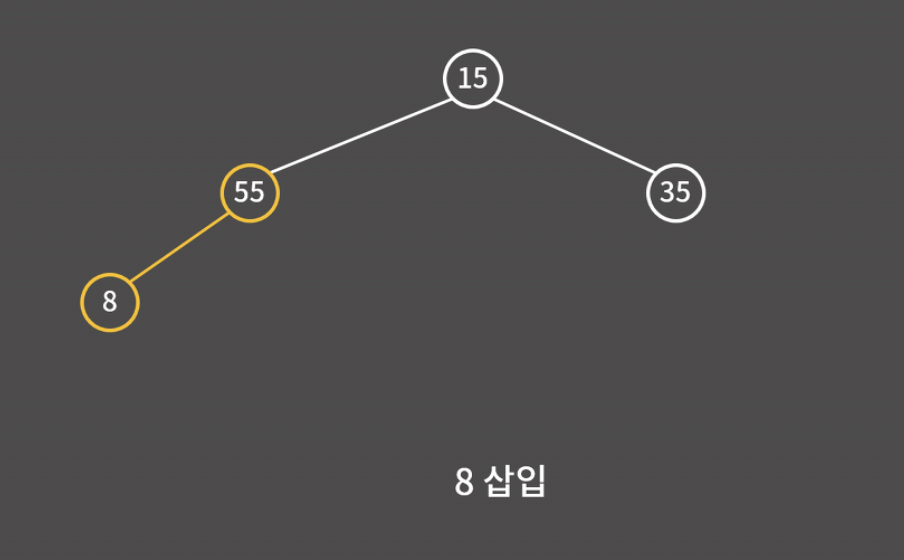
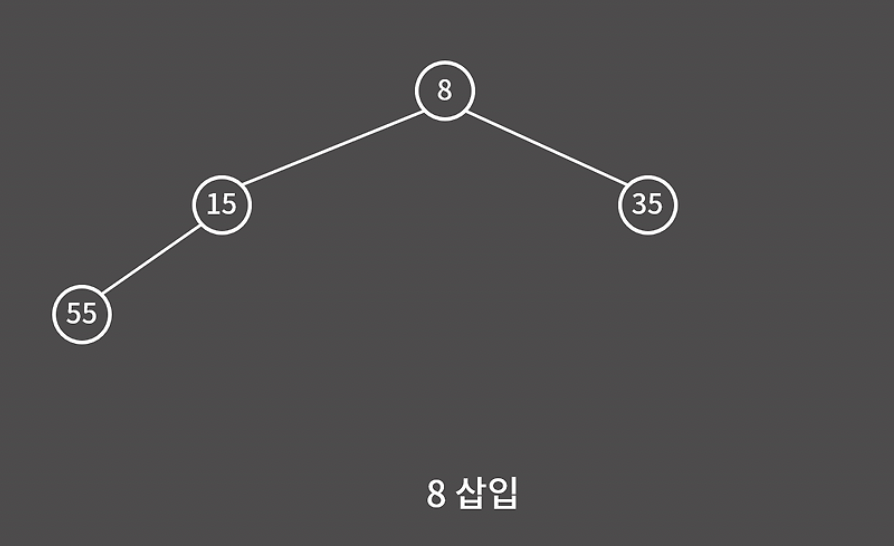
8을 삽입할 때도 마찬가지로 부모가 자식보다 작을 때까지 계속해서 자리를 바꿔주면 된다.
원소를 삽입할 때마다 아무리 대소 비교를 많이 해도 트리의 최대 높이까지만 올라가서 자리를 바꿔주면 되기 때문에 삽입의 시간복잡도는 O(logN)이 된다.
fetch
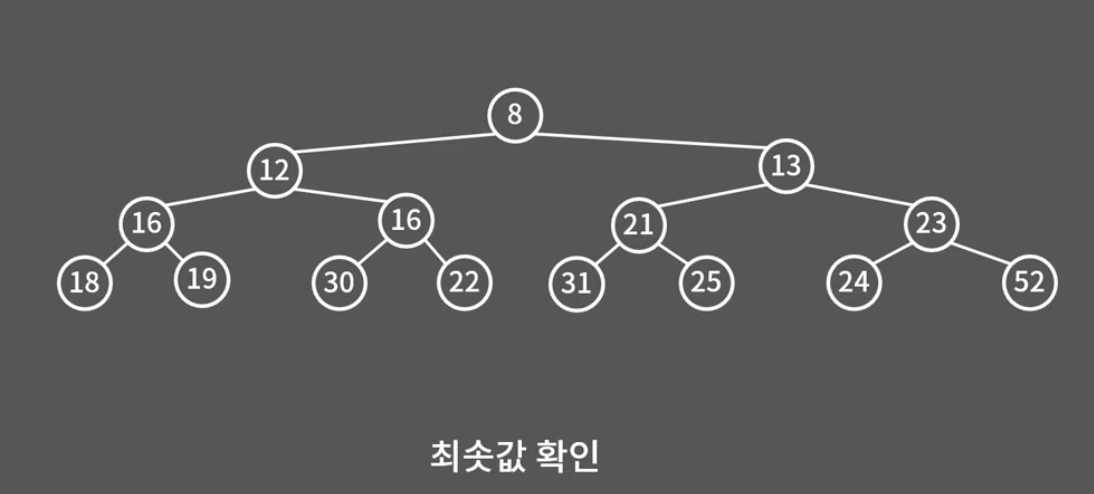
최솟값의 확인은 매우 간단하다. 그냥 루트 노드를 확인하면 된다. 단, 주의할 점은 최소 힙에서는 최솟값을 효율적으로 확인할 수 있지만, 열번째로 작은 값 또는 최댓값의 확인은 모든 원소를 다 확인하지 않는 한 불가능하다는 것이다. 최대 힙도 마찬가지이다. 이러한 점 또한 이진 검색 트리와의 차이라고 볼 수 있다.
erase
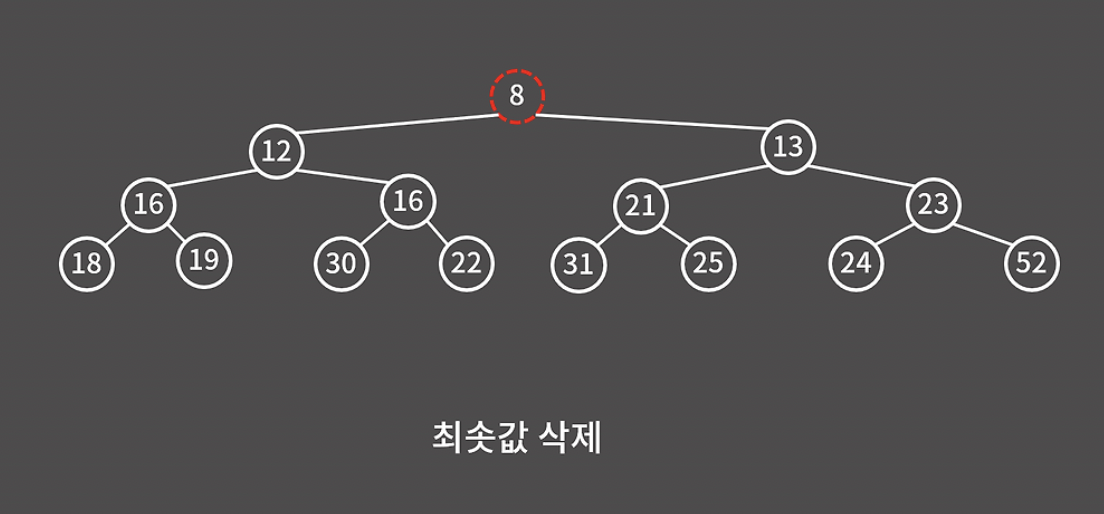
그냥 무턱대고 원소를 지웠다가는 트리 구조가 깨지기 때문에 뭔가 방법을 생각해야 한다.
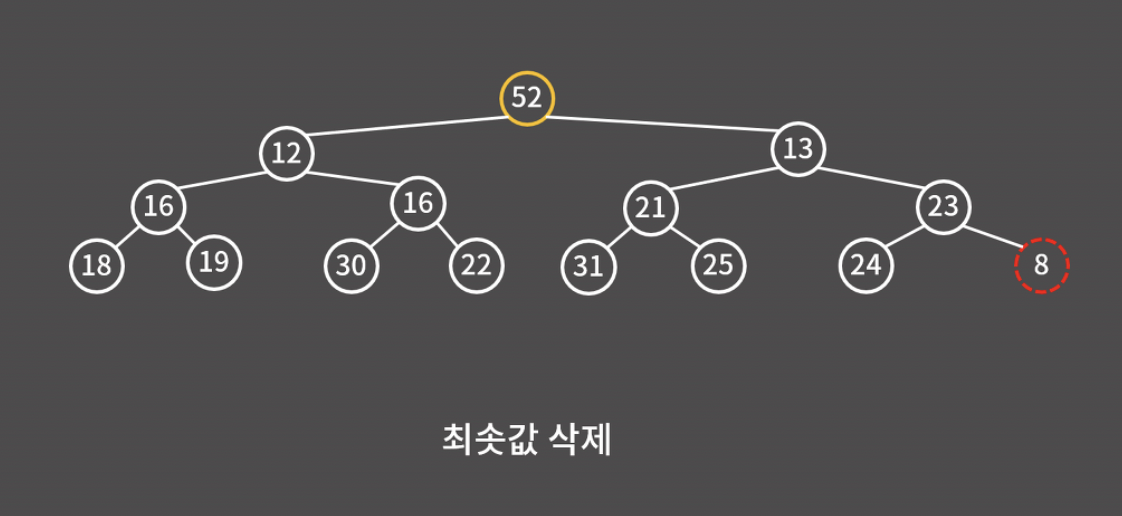
트리 구조 상에서 가장 마지막 위치인 52와 8의 자리를 바꾸고 8을 제거하면 된다. 그러면 8의 자식이 없기 때문에 트리 구조가 잘 유지된다.
그런데 52가 루트 노드가 되면 최소 힙의 조건에 위배되므로 조치가 필요하다.
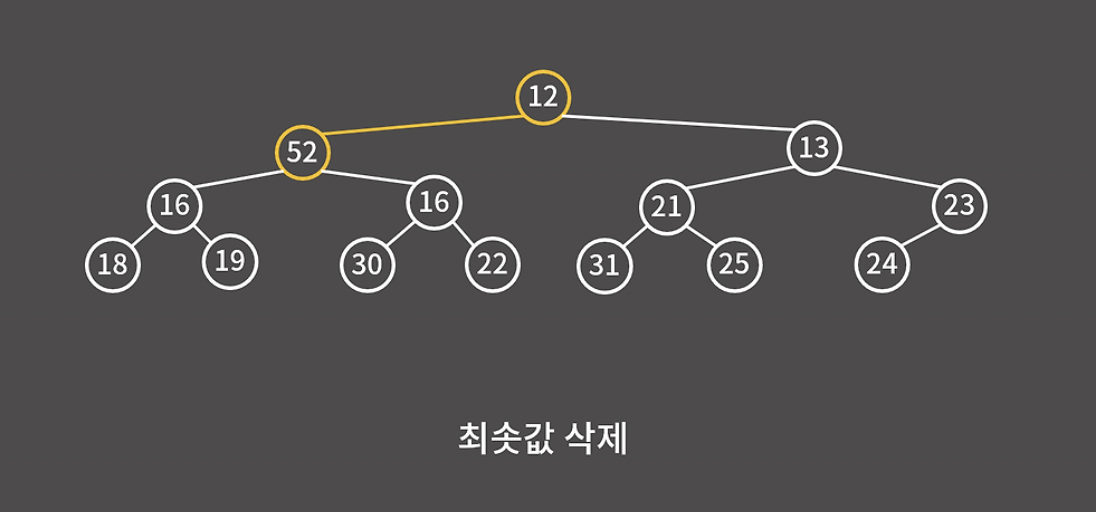
52와 그 자식 노드 중에 가장 작은 값을 루트 노드로 올린다.
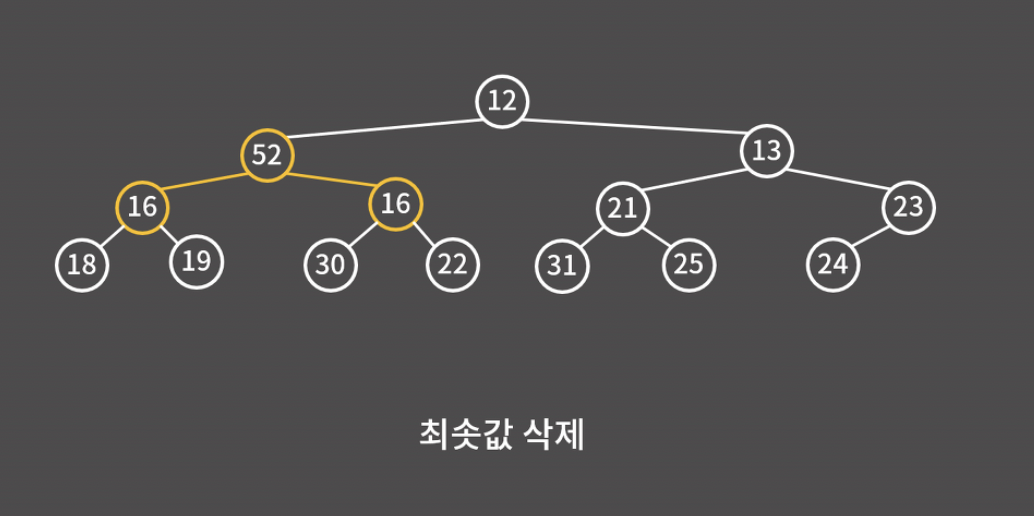
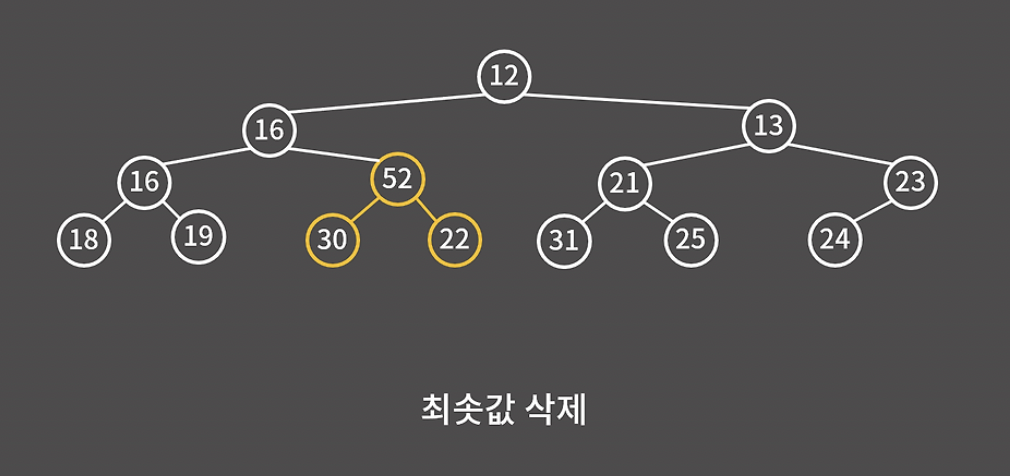
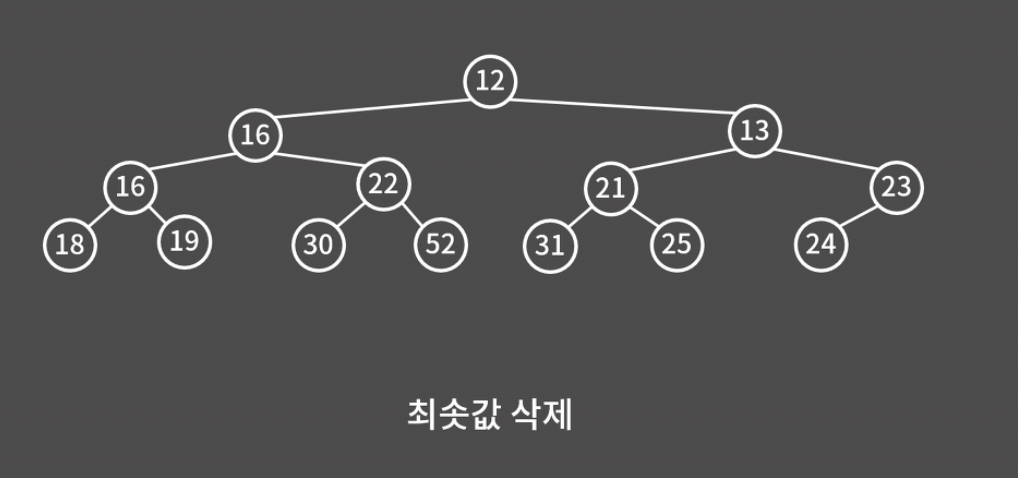
그 아래 노드들에 대해서도 부모가 자식보다 작을 때까지 계속해서 자리를 바꿔주면 된다.
최소 힙 구현
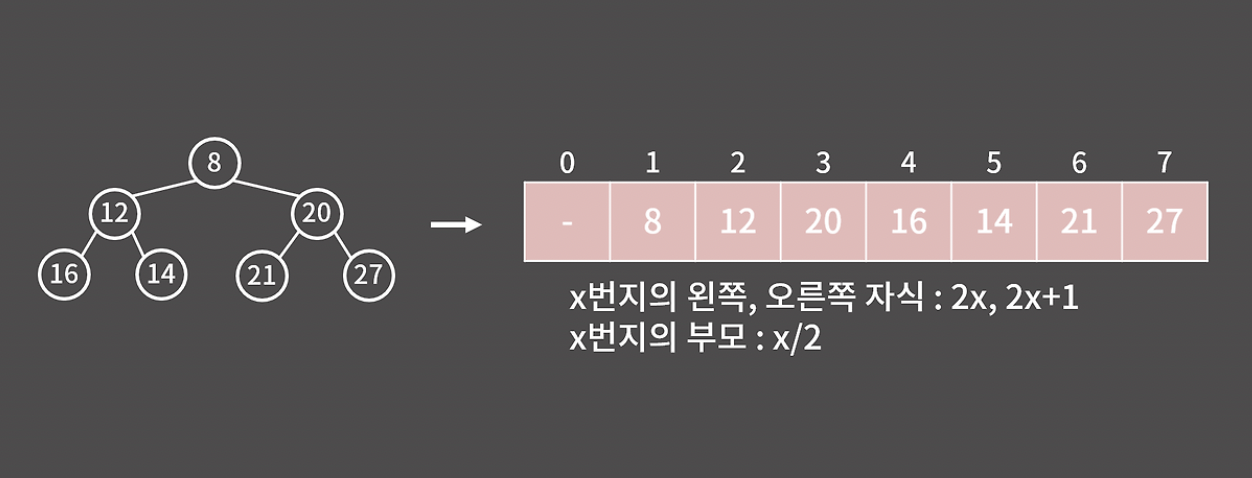
각 원소를 배열로 대응시켜 위와 같이 간단히 표현할 수 있다. x번지의 왼쪽, 오른쪽 자식은 각각 2x, 2x + 1 번지이고, 부모는 x/2 번지가 된다.
#include <bits/stdc++.h>
using namespace std;
int heap[100005];
int size = 0; // heap에 들어있는 원소 수
// 삽입 O(logN)
void push(int x) {
heap[++size] = x; // 트리에 노드 추가
int idx = size;
while(idx != 1) { // 루트 노드 자리에 도달할 때까지 반복
int parent = idx / 2;
if(heap[parent] <= heap[idx]) break;
swap(heap[parent], heap[idx]); // 부모가 자식보다 작도록 스왑
idx = parent;
}
}
// 최솟값 확인 O(1)
int top() {
return heap[1];
}
// 삭제 O(logN)
void pop() {
heap[1] = heap[size--]; // 루트 노드와 자리 바꾸고, 마지막 원소 삭제
int idx = 1;
// 왼쪽 자식의 인덱스가 size보다 크면 idx는 잎 노드
while(2 * idx <= size) {
int lc = 2 * idx, rc = 2 * idx + 1;
int minChild = lc; // 두 자식 중에 작은 값의 인덱스 저장
if(rc <= size && heap[rc] < heap[lc])
minChild = rc;
if(heap[idx] <= heap[minChild]) break;
swap(heap[idx], heap[minChild]);
idx = minChild;
}
}STL priority_queue
#include <bits/stdc++.h>
using namespace std;
int main() {
priority_queue<int> pq; // 최대 힙
// priority_queue<int, vector<int> greater<int>>로 선언 시 최소 힙
pq.push(10);
pq.push(2);
pq.push(5);
pq.push(9); // {10, 2, 5, 9}
cout << pq.top() << '\n'; // 10
pq.pop(); // {2, 5, 9}
cout << pq.size() << '\n'; // 3
if(pq.empty()) cout << "pq is empty\n";
else cout << "pq is not empty\n";
pq.pop(); // {2, 5}
cout << pq.top() << '\n'; // 5
}Q. priority_queue에서 할 수 있는 건 어차피 set에서도 할 수 있고, 시간복잡도도 동일하지 않나요? 그러면 set이 제공하는 기능이 더 많은데 priority_queue를 사용할 이유가 있나요?
A. 맞는 말이지만 priority_queue는 set보다 수행 속도가 더 빠르고 공간도 더 적게 차지합니다.
set은 이전 글에서 설명한 것처럼 새 정점을 동적으로 할당하거나 정점을 제거하고 불균형이 발생했을 때 이에 대한 처리가 필요해서 O(logN)이어도 시간이 꽤 걸리는 작업이다. 반면, priority_queue는 트리 자체가 불균형이 없고 무조건 logN번 비교하면서 자리를 바꾸는 것이기 때문에 훨씬 속도가 빠르다. 같은 연산 수행 시 set, priority_queue는 속도가 한 2~4배 정도 차이가 날 수 있다. 그리고 공간을 차지하는 정도도 차이가 많이 난다. 따라서 priority_queue에서 제공하는 연산만 필요한 경우에는 set을 쓰는 것보다 priority_queue를 사용하는 게 더 좋다.
연습문제
11286번. 절댓값 힙
https://www.acmicpc.net/problem/11286
#include <iostream>
#include <queue>
using namespace std;
// 절댓값을 기준으로 하는 최소 힙 (절댓값이 같으면 원래 값을 기준으로)
class cmp {
public:
bool operator() (int a, int b) {
// 작은 노드가 부모가 되도록 스왑
if(abs(a) != abs(b)) return abs(a) > abs(b);
return a > 0 && b < 0;
}
};
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
priority_queue<int, vector<int>, cmp> pq;
int n;
cin >> n;
while(n--){
int x;
cin >> x;
if(x == 0){
if(pq.empty()) cout << "0\n";
else {
cout << pq.top() << "\n";
pq.pop();
}
}else{
pq.push(x);
}
}
}참고로 힙을 이용하면 N개의 원소를 삽입했다가 크기 순으로 빼는 방식으로 O(NlogN)에 N개의 원소를 정렬할 수 있으며, 이를 힙 정렬이라고 한다. 그리고 다익스트라 알고리즘에서 최단 거리가 가장 작은 노드를 탐색하고 제거할 때도 우선순위 큐를 이용하면 시간복잡도를 줄일 수 있다.

