문제

https://www.acmicpc.net/problem/11051

---

이항 계수

이항계수 (Binomial Coefficient)는 조합론에서 등장하는 개념으로, 주어진 크기 집합에서 원하는 개수만큼 뽑는 조합의 경우의 수를 의미한다. 2를 상징하는 ‘이항’이라는 말이 붙은 이유는 하나의 아이템에 대해서는 ‘뽑거나, 안 뽑거나’ 두 가지의 선택만이 있기 때문이다.

집합의 전체 원소의 개수 n에 대해 k개의 아이템을 뽑는 이항계수(조합의 수)는 다음과 같이 정의한다.

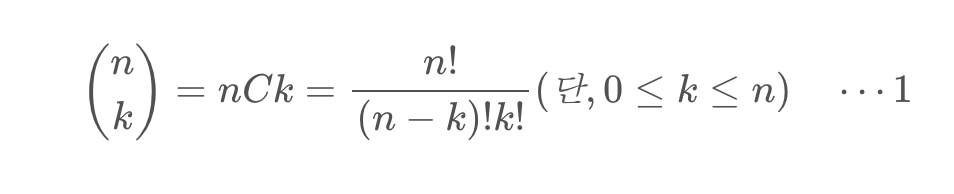
추가적으로 중요한 이항계수의 성질은 다음과 같다.

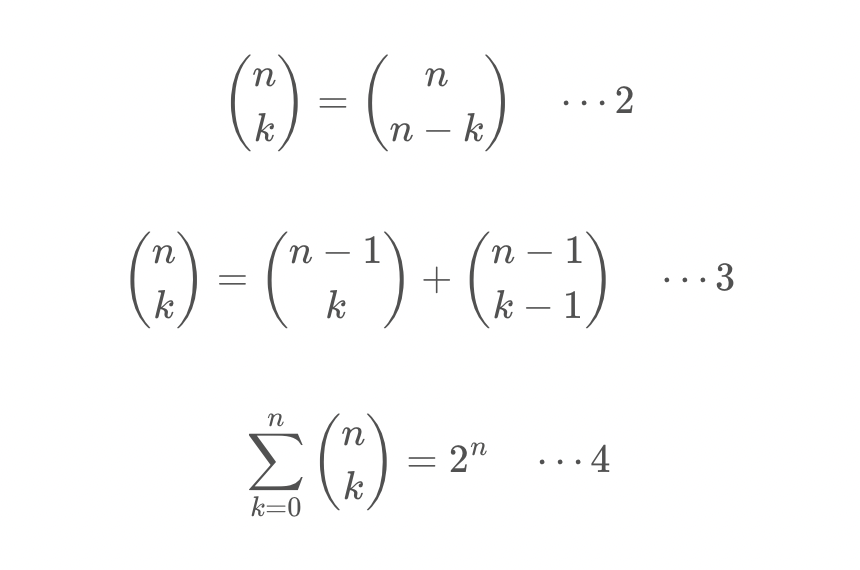
이번 문제는 위의 성질 중에서 2, 3번을 이용하여 풀이할 것이다.

풀이

void bino_coef(int n, int k) {
    if (k == 0 || n == k) return 1;
    return bino_coef(n-1, k) + bino_coef(n-1, k-1);
}

위의 코드와 같이 재귀함수를 이용하여 이항계수를 구하면, 동일한 부분 문제를 반복적으로 호출하며 매우 비효율적인 연산을 하게 된다.

따라서, 크기가 (N + 1) * (K + 1) 인 2차원 테이블에 부분문제의 해를 저장해두는 '메모이제이션 기법'을 사용할 것이다.

이항계수의 2번 성질에 의하면, nC0 = nCn = 1 이다. 즉, 2차원 테이블에서 열이 0인 경우, 그리고 행과 열의 인덱스가 동일한 경우에 해당한다.

3번 성질에 의하면, 다음과 같이 부분문제의 해를 모아서 큰 문제의 해를 구할 수 있다.

dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]

이 문제에서는 덧셈 연산의 결과가 너무 커지는 것을 방지하기 위해 10007로 나눈 나머지를 테이블에 저장한다.

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cmath>
#include <map> 
using namespace std;
typedef pair<int, int> pii; 
typedef long long ll;

const int MAX = 1001; 
int N, K;
ll dp[MAX][MAX];

void input() {
	cin >> N >> K;
}

void solution() {
	for(int i = 1; i <= N; i++){
		for(int j = 0; j <= K; j++){ 
			if(j == 0 || i == j) dp[i][j] = 1; 
			else dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j]) % 10007; 
		}
	}

	cout << dp[N][K]; 
}

int main() {
	ios_base::sync_with_stdio(0);
	cin.tie(0);

	input(); 
	solution(); 
	
	return 0;
}

참고자료

https://shoark7.github.io/programming/algorithm/3-ways-to-get-binomial-coefficients