문제

https://www.acmicpc.net/problem/5557

---

풀이

문제에 주어진 예시를 통해 풀이 방법을 고안해보자.

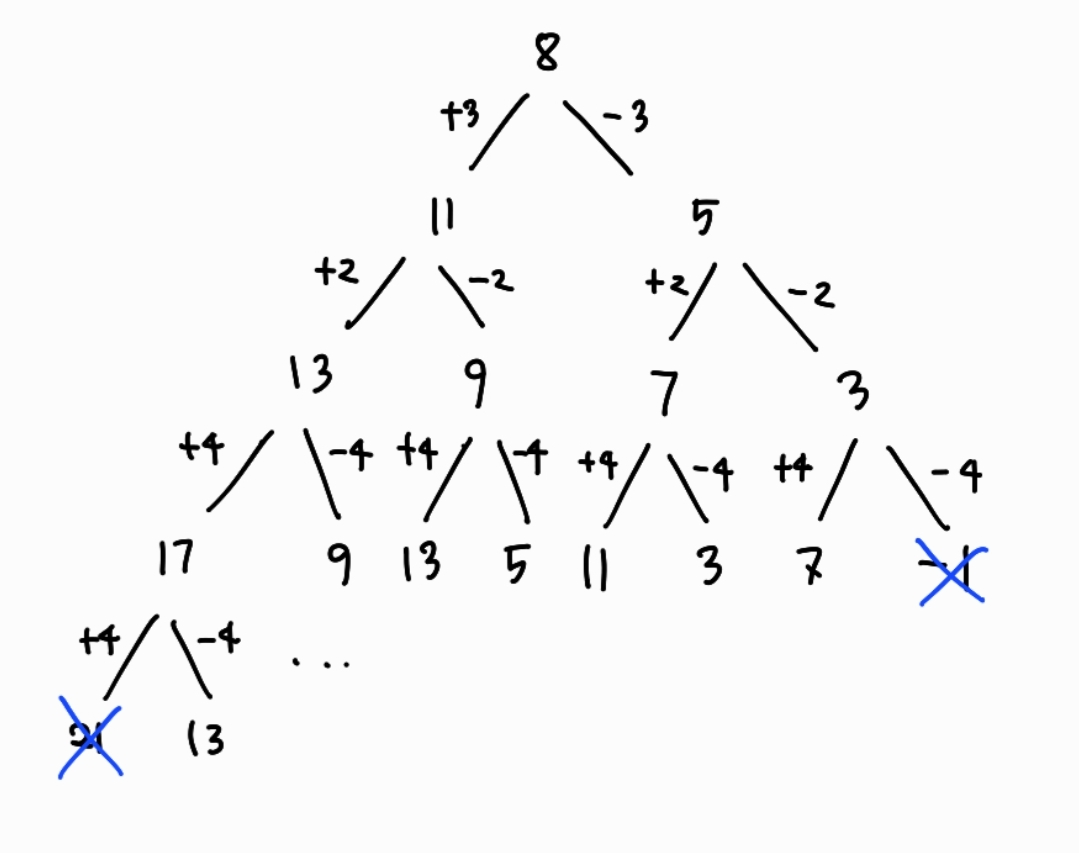
위의 그림처럼 N개의 원소에 대해 덧셈/뺄셈 연산을 반복적으로 수행하면, 시간복잡도는 O(2^N)이 될 것이다. N이 30까지만 커져도 약 10억 가량의 연산을 수행해야 하는 매우 비효율적인 방법이다.

따라서 덧셈/뺄셈 연산 결과를 별도의 테이블에 저장해두고 (메모이제이션), 다른 경우의 수에 대한 연산을 수행할 때 이미 계산된 결과가 있으면 테이블에 저장된 값을 그대로 사용하여 시간복잡도를 줄일 수 있다!

이처럼 dp 문제는 주어진 문제가 아래와 같은 조건을 만족시키는지 파악하는 것이 매우 중요하다!

1. 최적 부분 구조 (Optimal substructure)
   큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아서 큰 문제를 해결할 수 있다.
2. 중복되는 부분 문제 (Overlapping subproblem)
   동일한 작은 문제를 반복적으로 해결한다.

top-down 방식

• 입력 크기의 최댓값: 100, 중간 연산 결과의 최댓값: 20 -> dp[101][21] 테이블 생성
• 등호를 붙여야 하는 위치 (idx - 2)에 도달할 때까지 덧셈 또는 뺄셈 연산을 수행하는 DFS 함수 재귀 호출
  • sum이 0보다 작거나 20보다 크면 return 0
  • dp 테이블에 저장된 값이 있는 경우 그대로 리턴
  • idx - 2 위치에 도달했을 때, 배열의 마지막 원소와 sum이 같은 값이면 return 1

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <unordered_set>
#include <set>
using namespace std;
typedef pair<int, int> pii; 
typedef long long ll;

const int N_MAX = 101; 
const int V_MAX = 21; 
ll dp[N_MAX][V_MAX];
ll arr[N_MAX];
int N; 

void input() {
	cin >> N; 

	for(int i = 0; i < N; i++){
		cin >> arr[i];
	}
}

ll dfs(int idx, int sum){
	if(sum < 0 || sum > 20) return 0; 

    // 복사 연산 수행하지 않도록 reference 사용
	ll& result = dp[idx][sum]; 
	if(result != 0) return result;

	if(idx == N - 2){
		if(arr[N - 1] == sum){
			return 1; 
		}
		return 0; 
	}

	result += dfs(idx + 1, sum + arr[idx + 1]);
	result += dfs(idx + 1, sum - arr[idx + 1]);

	return result; 
}

void solution() {
	cout << dfs(0, arr[0]);
}

int main() {
	ios_base::sync_with_stdio(0);
	cin.tie(0);

	input(); 
	solution(); 
}