문제
국민대학교 홍보대사 국희는 여름방학을 맞아 고등학생들을 대상으로 학교 내부에 있는 건물을 소개해주는 일을 하게 되어 학교 건물을 차례로 소개할 수 있는 이동 경로를 짜보기로 하였다. 국민대학교는 북한산의 정기를 받는 위치에 있어 건물 간 연결된 길이 험난한 오르막길일 수도 있고, 내리막길일 수도 있다. 국희는 먼저 입구를 기준으로 건물 간 연결된 도로가 오르막길인지, 내리막길인지를 파악하여 오르막길인 경우 점선, 내리막길인 경우 실선으로 표시하였다.
그림 1
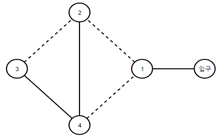
건물을 구분하기 쉽도록 번호를 붙였고, 입구에는 숫자 0을 붙이기로 하였다. 그 다음 모든 건물을 방문하는 데 필요한 최소한의 길을 선택하여, 해당 길을 통해서만 건물들을 소개하기로 하였다. 이 과정은 굉장히 신중해야 하는데, 오르막길이 많이 포함되게 되면 굉장히 피곤해지기 때문이다.
얼마나 피곤해지는지 알아보기 위해 피로도를 계산하기로 하였다. 오르막길을 k번 오를 때, 피로도는 k^2이 된다. 피로도의 계산은 최초 조사된 길을 기준으로만 한다. 즉, 내리막길로 내려갔다 다시 올라올 때 오르막길이 되는 경우는 고려하지 않는다. 입구는 항상 1번 건물과 연결된 도로를 가지며, 출발은 항상 입구에서 한다.
그림 2
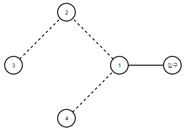
그림 3
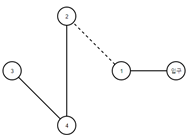
그림 1에서 모든 건물을 소개하기 위해 거쳐야 할 최소한의 도로는 4개임을 알 수 있다.
다음 2개의 그림은 그 4개의 도로를 뽑은 각각의 경우이다.
- 그림 2는 학교를 소개하는 데 총 3개의 오르막길을 오르게 되며 피로도가 9가 되는 최악의 코스가 된다.
- 그림 3은 오르막길을 1번만 오르게 되므로 학생들의 피로도는 1이 되는 최적의 코스가 된다.
- 이 경우 최악의 코스와 최적의 코스간 최종 피로도의 차이는 8이 된다.
국희는 최고의 프로그래머인 당신에게 위와 같은 방식으로 최악, 최선의 경로 간 피로도의 차이를 계산하는 프로그램의 제작을 부탁하였다. 프로그램을 작성하여 국희를 도와주자.
입력
입력 데이터는 표준 입력을 사용한다. 입력은 1개의 테스트 데이터로 구성된다.
입력의 첫 번째 줄에는 건물의 개수 N(1 ≤ N ≤ 1,000)과 도로의 개수 M(1 ≤ M ≤ N(N-1)/2) 이 주어진다.
입력의 두 번째 줄부터 M+1개의 줄에는 A, B(1 ≤ A, B ≤ N), C 가 주어진다. 이는 A와 B 건물에 연결된 도로가 있다는 뜻이며, C는 0(오르막길) 또는 1(내리막길)의 값을 가진다.
같은 경로 상에 2개 이상의 도로가 주어지는 경우는 없으며, 입구는 항상 1번 건물과 연결되어 있다. 입구와 1번 도로 간의 연결 관계는 항상 2번째 줄에 주어진다. 입구에서 모든 건물로 갈 수 있음이 보장된다.
출력
출력은 표준 출력을 사용한다. 입력받은 데이터에 대해, 주어진 조건을 만족하는 최악의 경로에서의 피로도와 최적의 경로 간 피로도의 차이를 출력한다.
예제
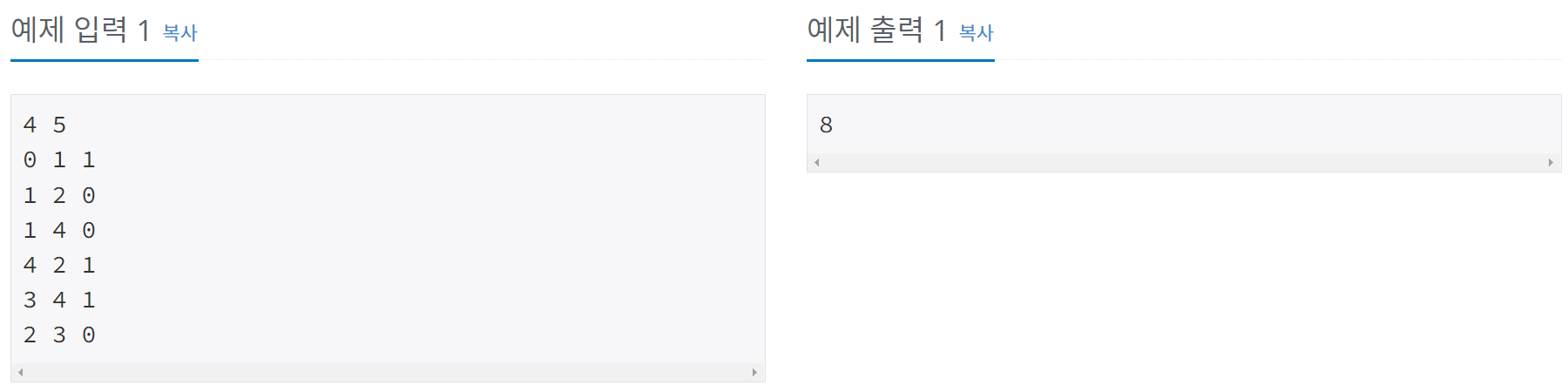
풀이
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
typedef pair<int, int> pii;
const int MAX = 1001;
int N, M;
vector<pair<int, pii>> edges;
int parent[MAX];
void input() {
cin >> N >> M;
// 부모 노드 배열 초기화
for(int i = 0; i <= N; i++){
parent[i] = i;
}
// (M + 1)개의 간선 정보 저장 -> 간선 개수 유의하기!!
for(int i = 0; i < M + 1; i++){
int a, b, c;
cin >> a >> b >> c;
edges.push_back({c, {a, b}});
}
}
// 루트 노드를 찾을 때까지 재귀 호출하고
// 배열에 루트 노드 번호를 저장한다.
int findRootNode(int x){
if(x == parent[x]) return x;
return parent[x] = findRootNode(parent[x]);
}
// 사이클을 만들지 않는 두 집합을 합친다.
void unionSet(int a, int b) {
if(a < b) parent[b] = a;
else parent[a] = b;
}
int kruskalForUphill() {
int cnt = 0;
// 오르막길부터 먼저 MST에 추가하기
for(int i = 0; i < edges.size(); i++){
int flag = edges[i].first;
int a = edges[i].second.first;
int b = edges[i].second.second;
int ra = findRootNode(a);
int rb = findRootNode(b);
if(ra != rb){
unionSet(ra, rb);
if(flag == 0) cnt++;
}
}
return cnt * cnt;
}
int kruskalForDownhill() {
int cnt = 0;
// 내리막길부터 먼저 MST에 추가하기
for(int i = edges.size() - 1; i >= 0; i--){
int flag = edges[i].first;
int a = edges[i].second.first;
int b = edges[i].second.second;
int ra = findRootNode(a);
int rb = findRootNode(b);
if(ra != rb){
unionSet(ra, rb);
if(flag == 0) cnt++;
}
}
return cnt * cnt;
}
void initParentArray() {
for(int i = 0; i <= N; i++){
parent[i] = i;
}
}
void solution() {
sort(edges.begin(), edges.end());
int maxFatigue = kruskalForUphill();
initParentArray();
int minFatigue = kruskalForDownhill();
cout << maxFatigue - minFatigue;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
input();
solution();
return 0;
}

