7576번 (2D 버전)

https://www.acmicpc.net/problem/7576

• 입력을 받으면서, 1의 위치를 모두 큐에 넣는다. (FIFO)
• 큐에서 1의 위치를 꺼내어 상하좌우에 0이 있는지 탐색한다.
• 0을 발견하면, 2차원 배열의 해당 위치에 0을 발견할 때까지 걸린 시간을 저장한다.
• 발견한 0은 1로 물들었으므로 큐에 1의 위치를 push 한다.
• 큐가 빌 때까지 모든 1에 대해 탐색을 진행했는데
  • 0이 남아있으면, -1 출력
  • 0이 모두 없어졌으면, 2차원 배열에 저장된 값 중에 최댓값 출력 (모든 0을 1로 물들이는 데 걸린 시간)
  • 이때 한 가지 주의할 점이 처음으로 0을 발견했을 때 그 위치에 저장되는 시간이 2이기 때문에, 최댓값에서 1을 빼줘야 정답이 된다.
  • 처음부터 모든 토마토가 익어서 1인 경우에는 배열의 값이 바뀌지 않은 상태에서 마지막에 -1을 하므로 정답인 0이 출력된다.

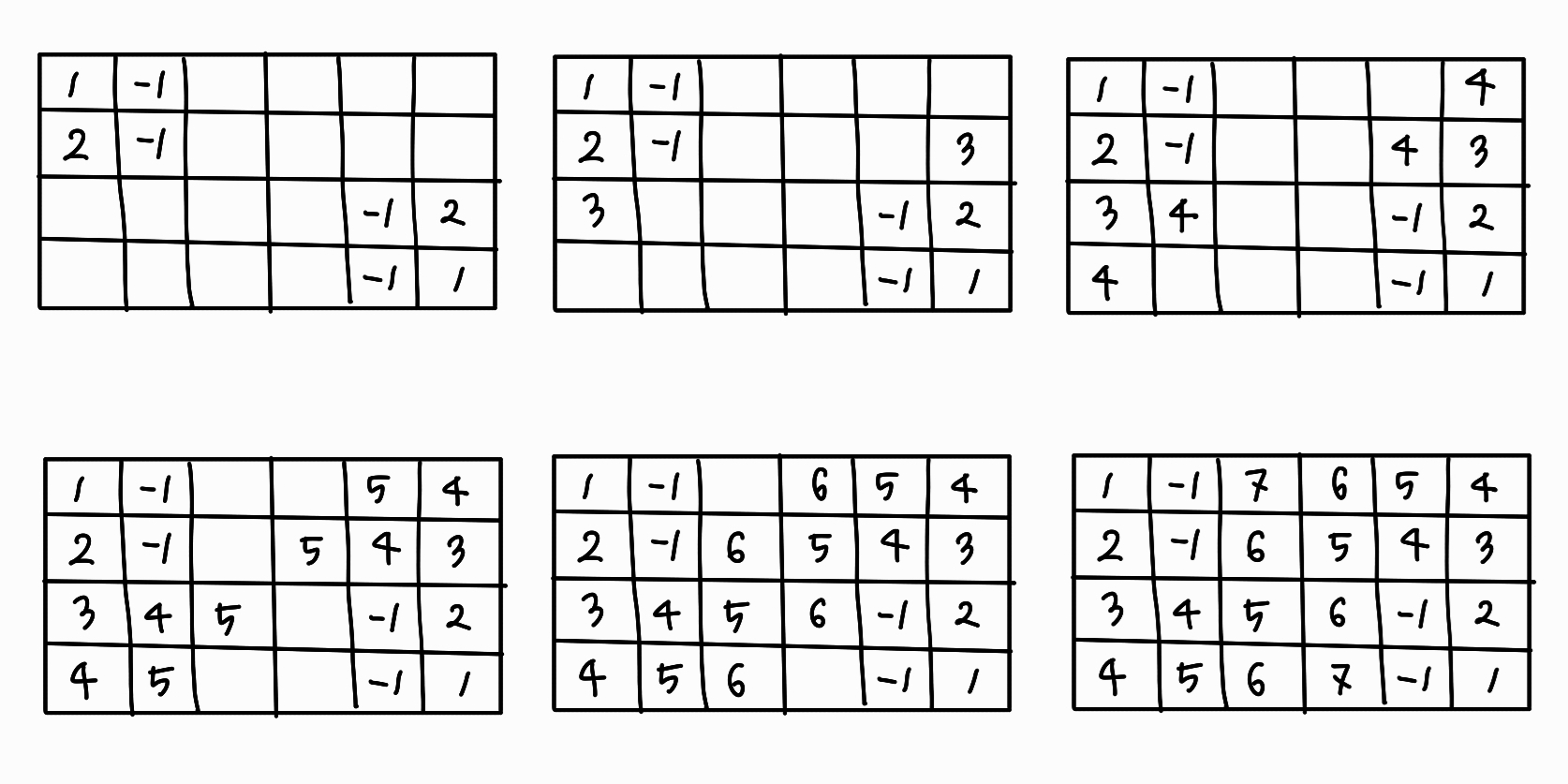
1의 위치를 큐에 저장하고 그 주변에 0이 있는지 탐색하는 것까지는 구현했는데, 큐에 time을 pair로 같이 묶어서 저장하거나 따로 time 변수를 만들어서 증가시키는 식으로 구현하니까 문제가 발생했다. 위의 그림처럼 1이 여러 개 있으면 그 주변의 0은 동시에 물들어야 한다. 그런데 큐에 1의 위치와 시간을 묶어서 같이 저장하고, 그 시간에 +1을 하는 식으로 구현하면 어떤 1의 위치에서 이미 time + 1을 했는데 다른 1의 위치에서 또 time + 1을 하게 된다. 따라서, 2차원 배열 자체에 graph[nx][ny] = graph[x][y] + 1 이런 식으로 걸린 시간을 업데이트 해나가야 한다. 마지막에 1을 빼주는 것도 잊지 말기!

#include <iostream> 
#include <vector> 
#include <string>
#include <algorithm>
#include <cstring> 
#include <queue> 
using namespace std;

const int MAX = 1001; 
int m, n; 
int graph[MAX][MAX];
queue<pair<int, int>> q; // 1의 좌표  

int dx[] = {-1, 1, 0, 0};
int dy[] = {0, 0, -1, 1};

void bfs() {
	while(!q.empty()){
		// 1의 위치를 하나씩 꺼내서 
		int x = q.front().first;
		int y = q.front().second;
		q.pop(); 

		// 상하좌우에 0이 있는지 탐색한다. 
		for(int i = 0; i < 4; i++){
			int nx = x + dx[i];
			int ny = y + dy[i];
			
			if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue; 

			// 0을 발견할 때까지 걸린 시간을 해당 위치에 저장 
			if(graph[nx][ny] == 0){ 
				graph[nx][ny] = graph[x][y] + 1; 

				// 0에서 1로 물든 토마토의 위치를 큐에 저장 
				q.push({nx, ny}); 
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	cin >> m >> n; // n x m 

	for(int i = 0; i < n; i++){
		for(int j = 0; j < m; j++){ 
			cin >> graph[i][j]; 

			// 1의 위치 저장 
			if(graph[i][j] == 1){
				q.push({i, j}); 
			}
		}
	}

	bfs(); 

	int ans = 0; 
	for(int i = 0; i < n; i++){
		for(int j = 0; j < m; j++){
			if(graph[i][j] == 0){
				cout << "-1\n";
				return 0; 
			}

			if(ans < graph[i][j]){
				ans = graph[i][j]; 
			}
		}
	}

	// 최댓값에서 1을 빼면 정답 
	cout << ans - 1; 
	
	return 0;
}

---

7569번 (3D 버전)

https://www.acmicpc.net/problem/7569

2차원 버전의 문제와 푸는 원리는 동일하며, 위아래 방향까지 탐색해야 한다는 것만 다르다!

#include <iostream> 
#include <vector> 
#include <string>
#include <algorithm>
#include <cstring> 
#include <queue> 
using namespace std;
typedef pair<int, int> pii; 

const int MAX = 101; 
int m, n, h; // 열, 행, 높이 
int graph[MAX][MAX][MAX]; // 높이(z), 행(x), 열(y)
queue<pair<int, pii>> q; // 1의 좌표 {z, {x, y}}

int dx[] = {-1, 1, 0, 0, 0, 0}; 
int dy[] = {0, 0, -1, 1, 0, 0};  
int dz[] = {0, 0, 0, 0, -1, 1};

void bfs() {
	while(!q.empty()){
		// 1을 하나씩 꺼내서 
		int z = q.front().first; 
		int x = q.front().second.first; 
		int y = q.front().second.second; 
		q.pop(); 

		// 상하좌우, 위아래에 0이 있는지 탐색한다.  
		for(int i = 0; i < 6; i++){
			int nx = x + dx[i];
			int ny = y + dy[i];
			int nz = z + dz[i];
			
			if(nx < 0 || nx >= n || ny < 0 || ny >= m || nz < 0 || nz >= h) continue; 

			// 0을 발견할 때까지 걸린 시간을 해당 위치에 저장 
			if(graph[nz][nx][ny] == 0){ 
				graph[nz][nx][ny] = graph[z][x][y] + 1; 

				// 0에서 1로 물든 토마토의 위치를 큐에 저장 
				q.push({nz, {nx, ny}}); 
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	cin >> m >> n >> h;

	for(int i = 0; i < h; i++){
		for(int j = 0; j < n; j++){
			for(int k = 0; k < m; k++){
				cin >> graph[i][j][k];
				
				if(graph[i][j][k] == 1){
					q.push({i, {j, k}});
				}
			}
		}
	}

	bfs(); 

	int ans = 0; 

	for(int i = 0; i < h; i++){
		for(int j = 0; j < n; j++){
			for(int k = 0; k < m; k++){
				if(graph[i][j][k] == 0){
					cout << "-1\n"; 
					return 0; 
				}

				if(ans < graph[i][j][k]){
					ans = graph[i][j][k]; 
				}
			}
		}
	}
			
	cout << ans - 1; 
	
	return 0;
}

2차원 버전에서는 MAX가 1000이어서 O(n^2) → 약 10^6

3차원 버전에서는 MAX가 100이어서 O(n^3) → 약 10^6

두 문제 모두 시간제한이 1초 (약 1억번의 연산) 인데, 입력 크기가 제한되어 있어서 각각 이중 for문, 삼중 for문으로 풀어도 시간초과가 발생하지 않는다.