문제
https://www.acmicpc.net/problem/14889
오늘은 스타트링크에 다니는 사람들이 모여서 축구를 해보려고 한다. 축구는 평일 오후에 하고 의무 참석도 아니다. 축구를 하기 위해 모인 사람은 총 N명이고 신기하게도 N은 짝수이다. 이제 N/2명으로 이루어진 스타트 팀과 링크 팀으로 사람들을 나눠야 한다.
BOJ를 운영하는 회사 답게 사람에게 번호를 1부터 N까지로 배정했고, 아래와 같은 능력치를 조사했다. 능력치 Sij는 i번 사람과 j번 사람이 같은 팀에 속했을 때, 팀에 더해지는 능력치이다. 팀의 능력치는 팀에 속한 모든 쌍의 능력치 Sij의 합이다. Sij는 Sji와 다를 수도 있으며, i번 사람과 j번 사람이 같은 팀에 속했을 때, 팀에 더해지는 능력치는 Sij와 Sji이다.
N=4이고, S가 아래와 같은 경우를 살펴보자.
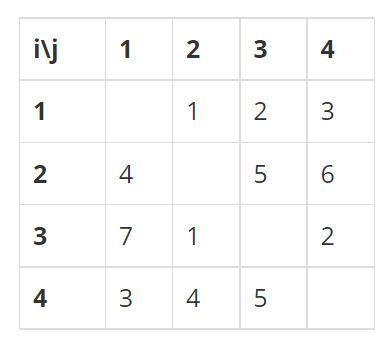
예를 들어, 1, 2번이 스타트 팀, 3, 4번이 링크 팀에 속한 경우에 두 팀의 능력치는 아래와 같다.
- 스타트 팀: S12 + S21 = 1 + 4 = 5
- 링크 팀: S34 + S43 = 2 + 5 = 7
1, 3번이 스타트 팀, 2, 4번이 링크 팀에 속하면, 두 팀의 능력치는 아래와 같다.
- 스타트 팀: S13 + S31 = 2 + 7 = 9
- 링크 팀: S24 + S42 = 6 + 4 = 10
축구를 재미있게 하기 위해서 스타트 팀의 능력치와 링크 팀의 능력치의 차이를 최소로 하려고 한다. 위의 예제와 같은 경우에는 1, 4번이 스타트 팀, 2, 3번 팀이 링크 팀에 속하면 스타트 팀의 능력치는 6, 링크 팀의 능력치는 6이 되어서 차이가 0이 되고 이 값이 최소이다.
입력
첫째 줄에 N(4 ≤ N ≤ 20, N은 짝수)이 주어진다.
둘째 줄부터 N개의 줄에 S가 주어진다. 각 줄은 N개의 수로 이루어져 있고, i번 줄의 j번째 수는 Sij 이다. Sii는 항상 0이고, 나머지 Sij는 1보다 크거나 같고, 100보다 작거나 같은 정수이다.
출력
첫째 줄에 스타트 팀과 링크 팀의 능력치의 차이의 최솟값을 출력한다.
예제
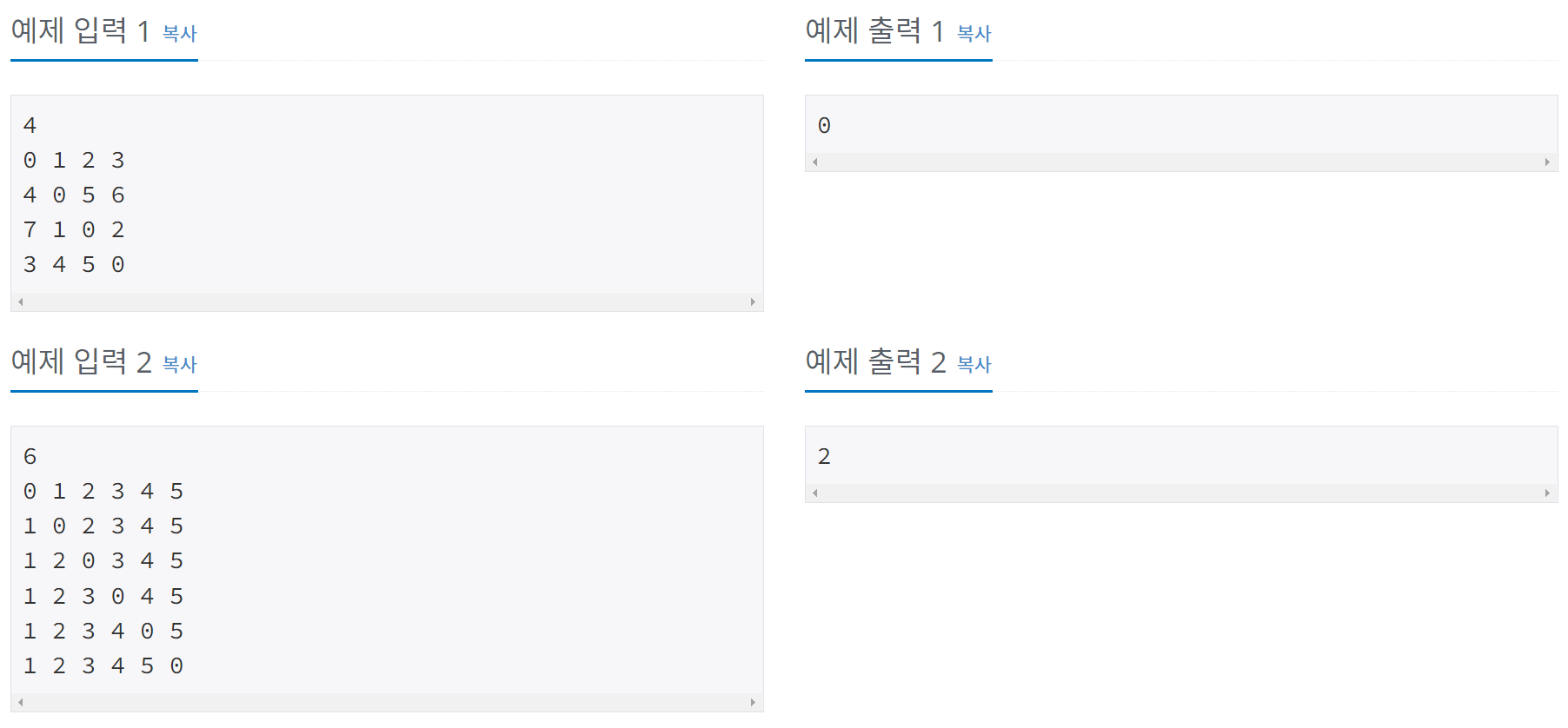
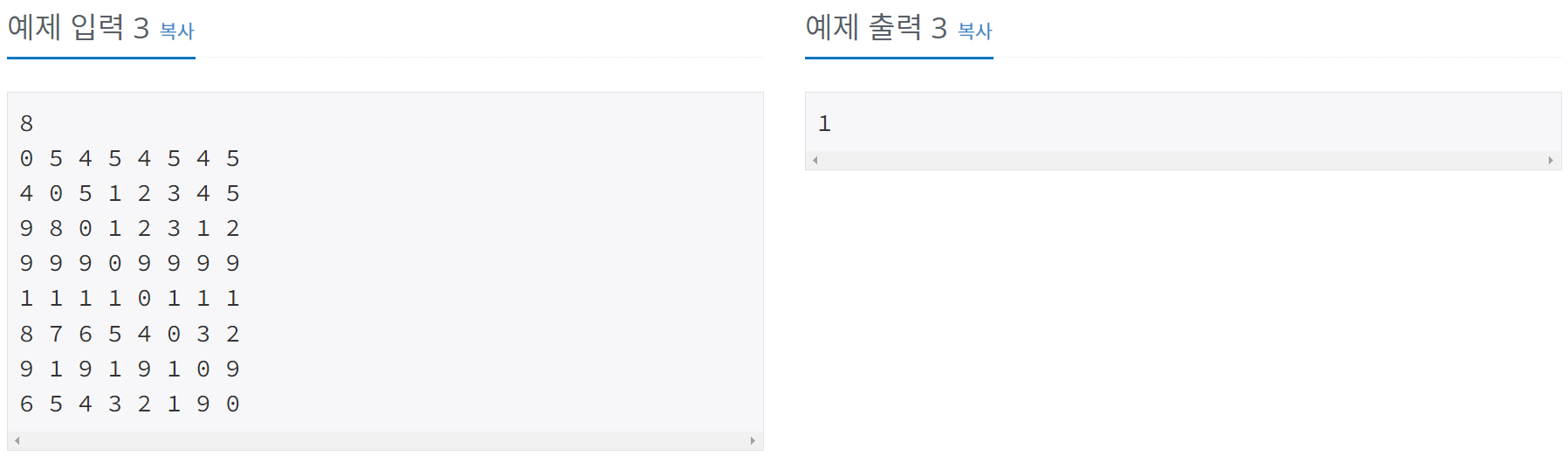
풀이
백트래킹
n개 중에 r개를 순서를 고려하지 않고 선택하는 조합을 백트래킹으로 어떻게 구현했는지 리마인드 해보자. 이와 비슷한 패턴으로 이 문제를 풀 수 있다. 이때 dfs 함수의 매개변수를 무엇으로 설정하느냐가 중요하다.
void dfs(int cnt, int idx) { // 현재까지의 결과, 탐색을 진행할 인덱스
// r개를 선택한 경우
if(cnt == r) {
// 결과 처리 후 현재 가지에 대한 탐색 종료
return;
}
// r개를 선택하지 않은 경우 재귀 호출 반복
for(int i = idx; i < n; i++){
if(!selected[i]){
selected[i] = true; // 상태 변화
dfs(cnt + 1, i); // 재귀 호출
selected[i] = false; // 다음 경우의 수를 위해 상태 복구
}
}
}답안
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int MAX = 20;
bool selected[MAX];
int arr[MAX][MAX];
int n;
int minVal = 1e9;
void input(){
cin >> n;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
cin >> arr[i][j];
}
}
}
void updateMinVal() {
vector<int> start, link;
int g1 = 0, g2 = 0;
for(int i = 0; i < n; i++){
if(selected[i]){
start.push_back(i);
}else{
link.push_back(i);
}
}
// 각 팀의 능력치 계산
// 각 팀원들의 번호에 맞는 행과 열을 뽑아서
// 그 2차원 배열의 모든 원소들의 합을 구하면 된다.
for(int i = 0; i < n/2; i++){
for(int j = 0; j < n/2; j++){
g1 += arr[start[i]][start[j]]; // 0~2: 00 01 02 10 11 12 20 21 22
g2 += arr[link[i]][link[j]]; // 3~5: 33 34 35 43 44 45 53 54 55
}
}
// 최소 차이 구하기
int gap = abs(g1 - g2);
if(gap < minVal){
minVal = gap;
}
}
void dfs(int cnt, int idx){ // 뽑은 개수, 탐색을 진행할 인덱스
if(cnt == n/2){
updateMinVal(); // 최솟값 갱신
return;
}
// n명 중에 n/2명을 선택하는 조합 구하기 (i는 idx부터 시작)
for(int i = idx; i < n; i++){
if(!selected[i]){
selected[i] = true;
dfs(cnt + 1, i);
selected[i] = false;
}
}
}
int main()
{
input();
dfs(0, 0);
cout << minVal;
return 0;
}

