문제

https://www.acmicpc.net/problem/1654

집에서 시간을 보내던 오영식은 박성원의 부름을 받고 급히 달려왔다. 박성원이 캠프 때 쓸 N개의 랜선을 만들어야 하는데 너무 바빠서 영식이에게 도움을 청했다.

이미 오영식은 자체적으로 K개의 랜선을 가지고 있다. 그러나 K개의 랜선은 길이가 제각각이다. 박성원은 랜선을 모두 N개의 같은 길이의 랜선으로 만들고 싶었기 때문에 K개의 랜선을 잘라서 만들어야 한다. 예를 들어 300cm 짜리 랜선에서 140cm 짜리 랜선을 두 개 잘라내면 20cm는 버려야 한다. (이미 자른 랜선은 붙일 수 없다.)

편의를 위해 랜선을 자르거나 만들 때 손실되는 길이는 없다고 가정하며, 기존의 K개의 랜선으로 N개의 랜선을 만들 수 없는 경우는 없다고 가정하자. 그리고 자를 때는 항상 센티미터 단위로 정수길이만큼 자른다고 가정하자. N개보다 많이 만드는 것도 N개를 만드는 것에 포함된다.

이때 만들 수 있는 최대 랜선의 길이를 구하는 프로그램을 작성하시오.

입력

첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 1만 이하의 정수이고, N은 1이상 100만 이하의 정수이다. 그리고 항상 K ≦ N 이다.

그 후 K줄에 걸쳐 이미 가지고 있는 각 랜선의 길이가 센티미터 단위의 정수로 입력된다. 랜선의 길이는 $2^{31} - 1$ (signed int 최댓값, 약 21억) 이하의 자연수이다.

출력

첫째 줄에 N개를 만들 수 있는 랜선의 최대 길이를 센티미터 단위의 정수로 출력한다.

예제

---

풀이

K개의 랜선을 최소 N개의 같은 길이의 랜선으로 자를 때, 자르는 랜선 길이의 최댓값을 구하는 문제이다. 자르는 랜선 길이가 너무 작으면 개수가 N개를 훌쩍 넘고, 자르는 랜선 길이가 너무 길면 개수가 N 이상이 되지 못한다. 즉, 아래와 같이 반비례 관계이다.

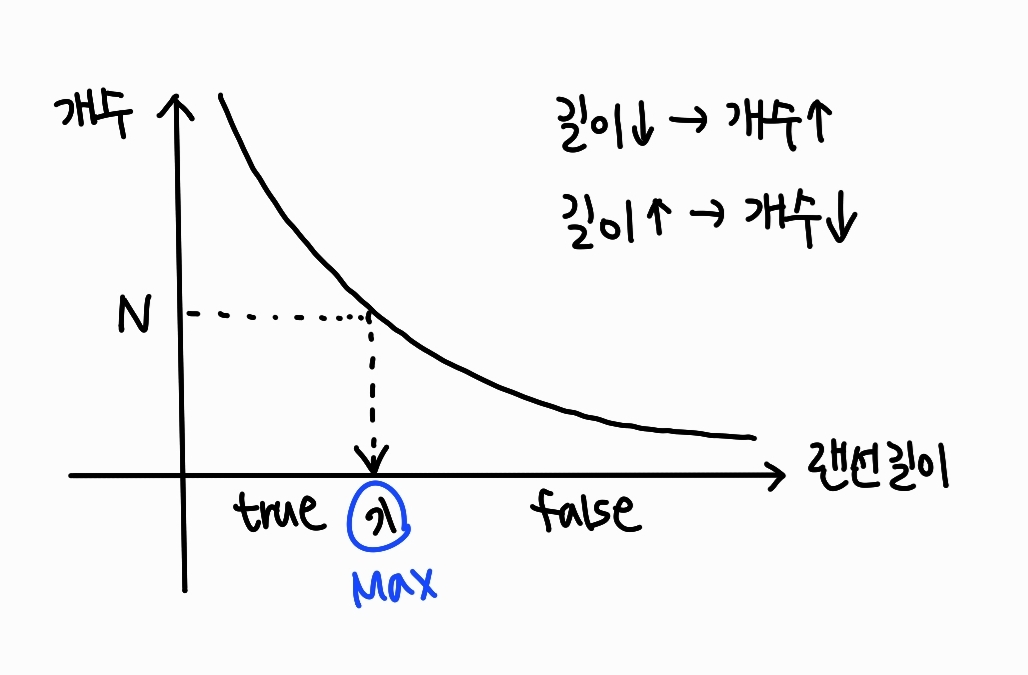
• lines: K개의 랜선 길이를 저장하는 배열
• optimize(lines, N): lines 배열에서 적어도 N개의 랜선을 만들기 위해 잘라야 하는 랜선 길이의 최댓값은?
• decision(lines, N, x): lines 배열에서 자르는 랜선 길이가 x일 때, 잘라진 랜선의 개수가 N개 이상인가?

최적화 문제를 결정 문제로 바꾸어 이진 탐색으로 해결하는 파라메트릭 서치를 적용해보자.

주의할 점은 랜선의 최대 길이가 INT_MAX에 해당하는 2147483647이기 때문에 lines 배열을 long long 타입으로 선언해줘야 정답 처리가 된다!

#include <iostream>
#include <string> 
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll; 

const int MAX = 10001; 
ll lines[MAX];
int K, N;

// 자르는 랜선 길이가 x일 때, 나오는 개수가 N개 이상인가?
bool decision(ll x){ 
	ll sum = 0; 
	for(int i = 0; i < K; i++){
		sum += lines[i] / x; 
	}
	return sum >= N;
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> K >> N; 

	for(int i = 0; i < K; i++){
		cin >> lines[i]; 
	}

	sort(lines, lines + K);
	ll left = 1; // 1부터 시작하는 것에 유의 
	ll right = lines[K - 1];

	ll ans = 0; 
	while(left <= right){
		ll mid = (left + right) / 2;
		
		if(decision(mid)) {
			ans = max(ans, mid); 
			left = mid + 1; 
		}
		else right = mid - 1; 
	}

	// 결정 문제를 만족시키는 x의 최댓값 출력 
	cout << ans;  

	return 0;
}