문제
https://www.acmicpc.net/problem/2805
상근이는 나무 M미터가 필요하다. 근처에 나무를 구입할 곳이 모두 망해버렸기 때문에, 정부에 벌목 허가를 요청했다. 정부는 상근이네 집 근처의 나무 한 줄에 대한 벌목 허가를 내주었고, 상근이는 새로 구입한 목재절단기를 이용해서 나무를 구할 것이다.
목재절단기는 다음과 같이 동작한다.
먼저, 상근이는 절단기에 높이 H를 지정해야 한다. 높이를 지정하면 톱날이 땅으로부터 H미터 위로 올라간다. 그 다음, 한 줄에 연속해있는 나무를 모두 절단해버린다.
따라서, 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다.
예를 들어, 한 줄에 연속해있는 나무의 높이가 20, 15, 10, 17이라고 하자. 상근이가 높이를 15로 지정했다면, 나무를 자른 뒤의 높이는 15, 15, 10, 15가 될 것이고, 상근이는 길이가 5인 나무와 2인 나무를 들고 집에 갈 것이다. (총 7미터를 집에 들고 간다) 절단기에 설정할 수 있는 높이는 양의 정수 또는 0이다.
상근이는 환경에 매우 관심이 많기 때문에, 나무를 필요한 만큼만 집으로 가져가려고 한다. 이때, 적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 나무의 수 N과 상근이가 집으로 가져가려고 하는 나무의 길이 M이 주어진다. (1 ≤ N ≤ 100만, 1 ≤ M ≤ 20억)
둘째 줄에는 나무의 높이가 주어진다. 나무의 높이의 합은 항상 M보다 크거나 같기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다. 높이는 10억 이하의 양의 정수 또는 0이다.
출력
적어도 M미터의 나무를 집에 가져가기 위해서 절단기에 설정할 수 있는 높이의 최댓값을 출력한다.
예제
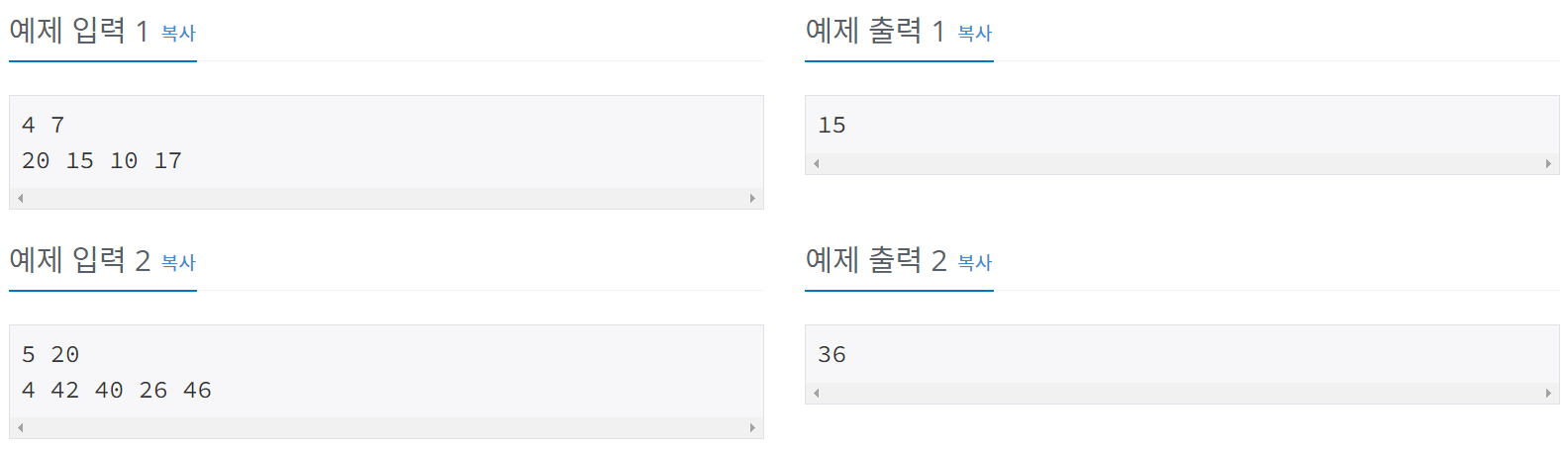
풀이
잘린 나무들의 길이 합이 최소 M미터가 되게 하는 절단기의 최대 높이를 구해야 한다.
절단기 높이가 너무 낮으면, 나무 길이의 합이 M미터를 훌쩍 넘어버릴 것이고,
절단기 높이가 너무 높으면, 나무 길이의 합이 M미터를 넘지 못할 것이다.
즉, 절단기 높이와 잘린 나무들의 길이 합은 반비례 관계이며, 이를 그래프로 나타내면 다음과 같다.
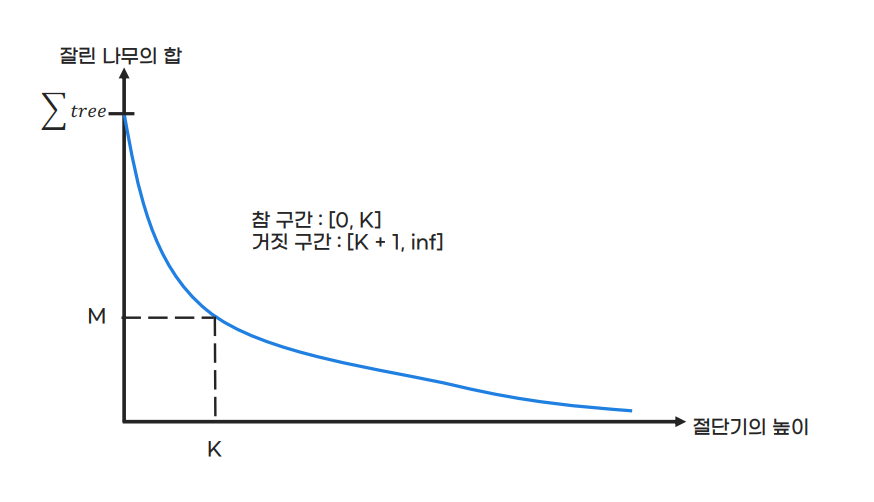
우리는 필요한 만큼만 나무를 잘라야 하기 때문에, 최소한 M미터는 챙겨갈 수 있게 하는 절단기의 최대 높이 K를 구해야 한다. 이러한 최적화 문제는 '결정 문제'로 바꾸어 생각해볼 수 있다.
📌 최적화 문제 vs. 결정 문제
최적화 문제는 최댓값, 최솟값 같은 최적의 해를 구하는 문제이고, 결정 문제는 답이 YES or NO 이 두 가지만 나오는 문제를 말한다. 최적화 문제를 푸는 방법이 있다면, 결정 문제는 무조건 풀 수 있기 때문에, 결정 문제는 최적화 문제보다 풀기 쉽다. 따라서, 이 문제를 풀기 위해 결정 문제를 먼저 정의하고 그것을 풀어서, 원래의 최적화 문제의 해를 구해보자!
-
optimize(tree, M) = 나무의 높이 배열 tree가 주어졌을 때, 나무를 자른 후 적어도 M미터의 나무를 챙겨가기 위한 절단기의 최대 높이를 구해라.
-
decision(tree, M, x) = 나무의 높이 배열 tree가 주어졌을 때, 절단기의 높이가 x인 경우 잘린 나무들의 길이 합이 M미터 이상인가? (답은 YES or NO)
우리는 decision(tree, M, x)를 만족시키는 x의 최댓값을 구하는 게 목표다.
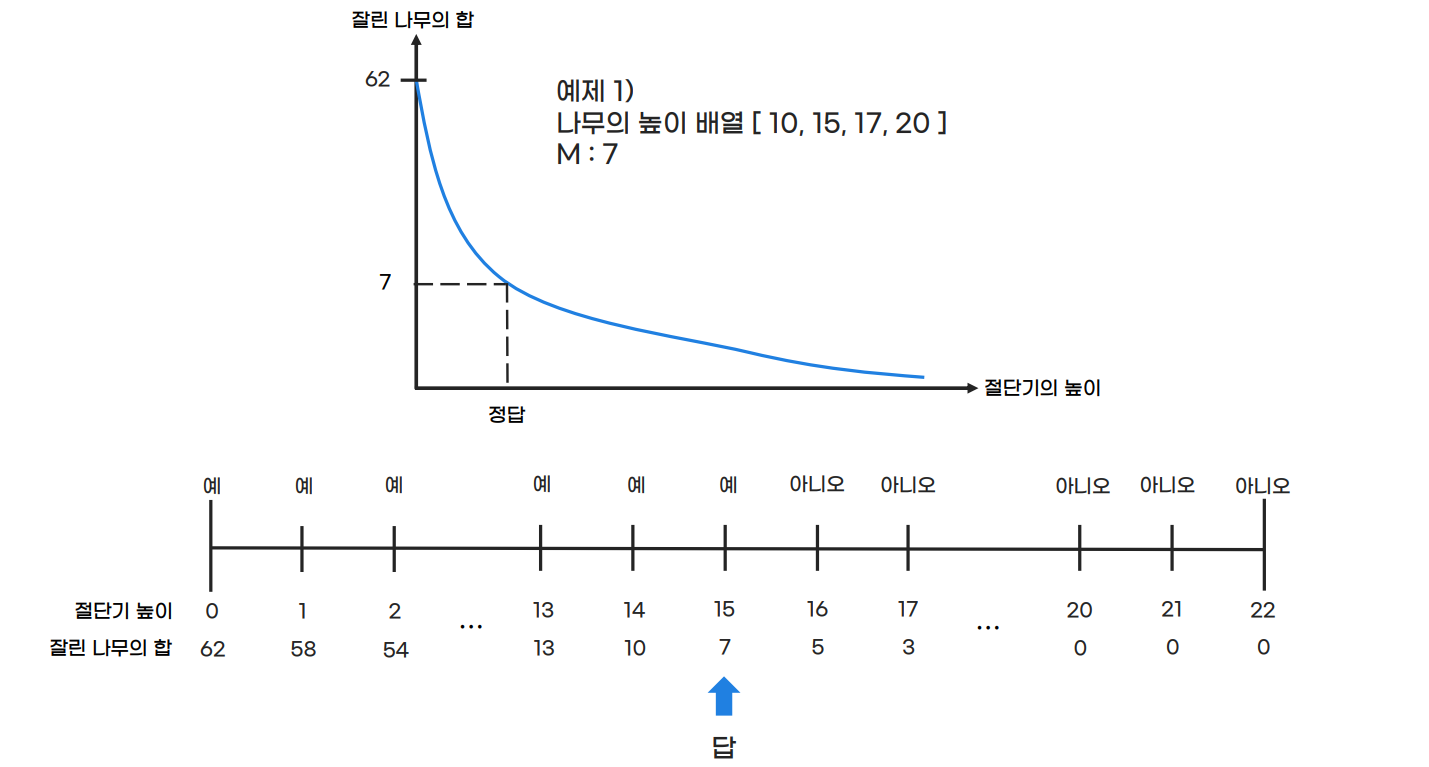
그래프에서 [0, K] 구간은 결정 문제에 대한 답이 true이고, [K + 1, INF) 구간은 false이다.
이렇게 결정 문제의 매개변수 (이 경우 K)에 대해 결정 문제의 답이 두 구간으로 나뉘는 것을 '이분적이다'라고 하며, 이런 경우 이분 탐색을 이용하여 결정 문제의 답이 달라지는 경계를 찾을 수 있다.
decision(x)를 만족하는 x의 최댓값을 이진 탐색으로 찾아보자.
low = 0, high = 1e9 (높이의 최댓값): 투 포인터 초기화while(low + 1 < high): low + 1 >= high 가 될 때까지 반복
decision(mid) == true -> low = mid- 가운데를 찍었는데 true라면, x의 최댓값을 구해야 하므로 low를 더 오른쪽으로 이동
decision(mid) == false -> high = mid- 가운데를 찍었는데 false라면, true 구간을 탐색하도록 high를 더 왼쪽으로 이동
- 반복문이 종료된 시점에서 True 구간의 최댓값을 가리키고 있는 low가 정답!
이처럼 최적화 문제를 결정 문제로 바꾸어 이진 탐색으로 해결하는 방법을 Parametric Search (파라메트릭 서치) 라고 부른다.
C++ 코드
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
using namespace std;
const int MAX = 1000001;
int tree[MAX];
int N, M;
// 절단기 높이가 x일 때, 잘린 나무 길이의 합이 M 이상인가?
bool decision(int x){
long long total = 0;
for(int i = 0; i < N; i++){
if(tree[i] > x){
total += tree[i] - x;
}
}
return total >= M;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> N >> M;
for(int i = 0; i < N; i++){
cin >> tree[i];
}
// 이진탐색은 정렬된 배열에만 적용 가능
sort(tree, tree + N);
// 절단기 높이 (결정 함수의 매개변수 x)
int low = 0;
int high = tree[N - 1];
while(low + 1 < high){
int mid = (low + high) / 2;
if(decision(mid)) low = mid;
else high = mid;
}
cout << low;
return 0;
}
파라메트릭 서치
-
decision(low) != decision(high)가 되도록 low, high의 초기값 잘 설정하기 -
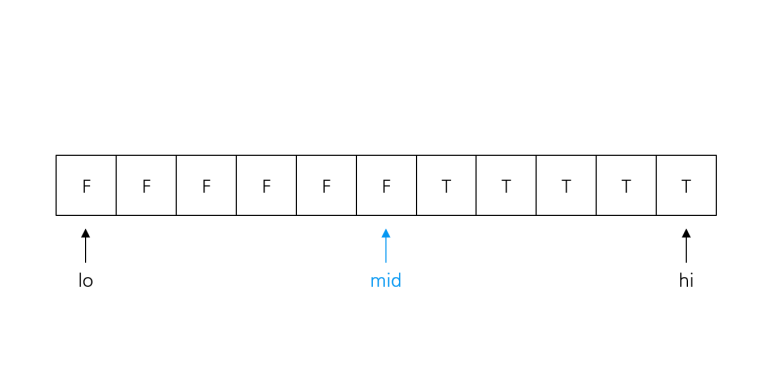
low + 1 < high인 동안mid = (low + high) / 2구해서decision(mid) == true라면low = mid, 아니라면high = mid반복한다.
우선 초기 상태의 low, high가 decision(low) != decision(high) 이므로, 결정 문제의 답이 바뀌는 경계는 [low, high] 내에 있음이 보장된다.
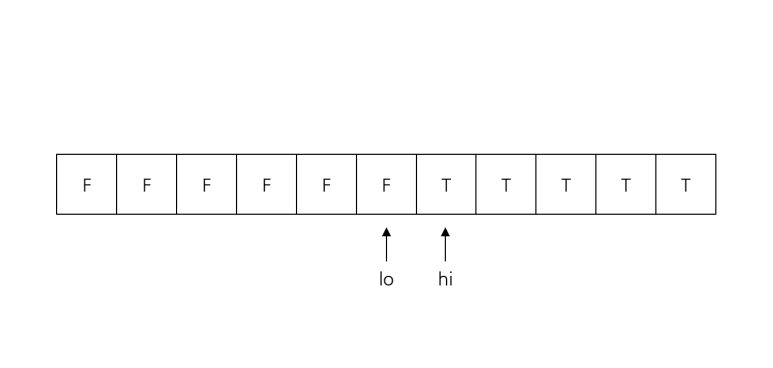
그리고 low + 1 < high 이기 때문에 low, high 사이에는 무조건 한 개 이상의 칸이 있으며, mid는 항상 low < mid < high를 만족한다. 따라서 구간의 길이는 매번 절반씩 줄어들어 언젠가 low + 1 == high가 되어 반복문을 탈출하게 된다.
이분 탐색이 끝나면 low, high는 결정 문제의 답이 바뀌는 경계에 위치하게 되며, 만약 결정 문제의 답 분포가 F~T인데 정답이 가장 큰 F라면 low를, 가장 작은 T라면 high를 출력해주면 된다.
decision(low) != decision(high)가 되도록 low, high 초기값 설정
decision(mid) == true라면 low = mid, 아니라면 high = mid 반복
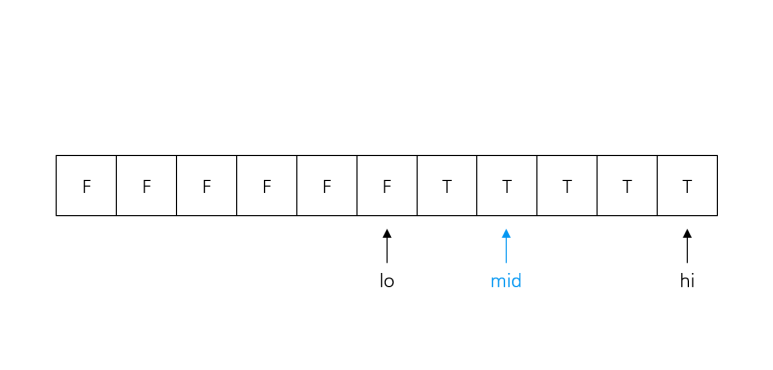
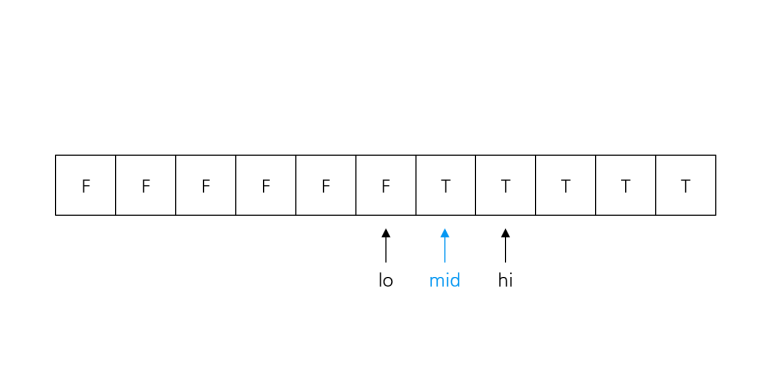
low + 1 == high가 되면 탈출, low, high는 경계에 위치
구현 시 유의사항
- lo, hi는 항상 정답의 범위를 나타낼 수 있도록 해야합니다. 예를 들어 lo를 출력해야 하는 문제의 답이 최대 n일 때 hi = n으로 선언하거나, hi를 출력해야 하는 문제의 답이 최소 0일 때 lo = 0으로 선언하면 안됩니다. (hi = n + 1, lo = -1로 선언해야 합니다)
- 오버플로우에 주의해야 합니다. 이분 탐색을 사용하는 문제는 대부분 수의 범위가 크기 때문에 오버플로우가 발생할 수 있습니다.
- 결정 문제의 정의에 맞게 Check함수를 잘 구현해야 합니다. 예를 들어 lower_bound는 v[i] >= k인 i의 최솟값을 구하는 함수이고, upper_bound는 v[i] > k인 i의 최솟값을 구하는 함수인데, Check 함수의 부등호를 조금만 틀려도 전혀 엉뚱한 값이 튀어나올 수 있습니다.

