[백준] 18430번. 무기 공학

leeeha·2024년 3월 10일

백준

목록 보기

153/186

문제

https://www.acmicpc.net/problem/18430

풀이

N, M의 최대 크기가 5이므로, 1부터 5까지 크기를 키워나가면서

주어진 나무 재료로 최대한 많은 부메랑을 만들 수 있는 경우의 수를 파악하려고 했다.

그러다가 부메랑 강도의 합을 최대로 만들 수 있는 규칙성이 발견되면 그리디로 풀고, 그렇지 않으면 DP로 풀어볼까 생각했다.

그런데 나무 재료가 정사각형이 아니기 때문에 N, M 크기에 따라 만들 수 있는 부메랑의 종류가 너무나도 제각각이었다. (가능한 경우의 수가 너무 많다.)

작은 문제의 해를 모아서 큰 문제의 해를 구하는 .. DP 문제인가 .. 점화식을 한번 세워볼까 생각해도 도저히 감이 잡히지 않았다.

결국 다른 사람 풀이를 참고해보니까 백트래킹으로 푸는 문제였다..!!!

알고리즘

부메랑 만들기

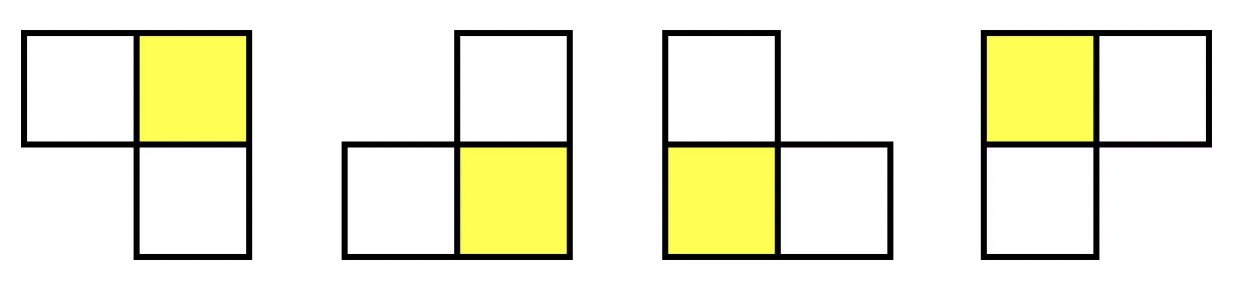
위의 그림에서 첫번째 부메랑 모양을 만들려면 중심이 되는 칸 (r, c)를 기준으로

(r, c - 1), (r + 1, c) 칸이 모두 NxM 범위 내에 있어야 하고
(r, c - 1), (r + 1, c) 칸이 다른 부메랑을 만드는 데 사용된 적이 없어야 한다. -> visited 배열 필요

나머지 부메랑 종류도 마찬가지이다.

다른 칸으로 이동하여 탐색

부메랑이 만들어지면 오른쪽으로 한칸 이동하여 다른 부메랑을 더 만든다.

3개의 칸의 방문여부를 확인한다.
문제의 조건에 맞게 부메랑의 강도를 계산한다.
오른쪽으로 한칸 움직이고, 현재까지의 부메랑 강도 합을 dfs 함수의 인자로 넣어 재귀호출한다.

4가지 부메랑 종류에 대한 처리

부메랑 모양에 맞게 위와 같은 백트래킹 알고리즘을 동일하게 수행한다.

경계 조건 처리 (+ 백트래킹 종료)

(c == m) 이면 오른쪽 끝까지 간 것이므로, 한 줄 밑의 맨 왼쪽부터 탐색을 시작한다.
(r == n) 이면 맨 아래 줄까지 모두 확인한 것이므로, 현재 경우의 수에 대한 부메랑 강도 합의 최댓값을 갱신한다.

C++ 코드

#include <iostream>
#include <string> 
#include <algorithm>
#include <vector>
#include <cmath>
#include <cstring>
using namespace std;

const int MAX = 6;
int N, M; 
int arr[MAX][MAX];
bool visited[MAX][MAX];
int ans = 0; 

// 우측 상단이 중심인 부메랑의 강도
int getRightTopPower(int r, int c) {
	return arr[r][c - 1] + arr[r + 1][c] + 2 * arr[r][c];
}

// 우측 하단이 중심인 부메랑의 강도
int getRightBottomPower(int r, int c) {
	return arr[r - 1][c] + arr[r][c - 1] + 2 * arr[r][c];
}

// 좌측 상단이 중심인 부메랑의 강도 
int getLeftTopPower(int r, int c) {
	return arr[r][c + 1] + arr[r + 1][c] + 2 * arr[r][c];
}

// 좌측 하단이 중심인 부메랑의 강도 
int getLeftBottomPower(int r, int c){
	return arr[r - 1][c] + arr[r][c + 1] + 2 * arr[r][c]; 
}

void dfs(int r, int c, int result){	
	if(c == M){
		c = 0; 
		r++;
	}

	if(r == N){
		ans = max(ans, result);
		return; 
	}

	if(!visited[r][c]){
		if(r + 1 < N && c - 1 >= 0 && !visited[r + 1][c] && !visited[r][c - 1]){
			visited[r][c] = true; 
			visited[r + 1][c] = true; 
			visited[r][c - 1] = true; 

			dfs(r, c + 1, result + getRightTopPower(r, c));

			visited[r][c] = false; 
			visited[r + 1][c] = false; 
			visited[r][c - 1] = false; 
		}

		if(r - 1 >= 0 && c - 1 >= 0 && !visited[r - 1][c] && !visited[r][c - 1]){
			visited[r][c] = true; 
			visited[r - 1][c] = true; 
			visited[r][c - 1] = true; 

			dfs(r, c + 1, result + getRightBottomPower(r, c));

			visited[r][c] = false; 
			visited[r - 1][c] = false; 
			visited[r][c - 1] = false; 
		}

		if(r + 1 < N && c + 1 < M && !visited[r + 1][c] && !visited[r][c + 1]){
			visited[r][c] = true; 
			visited[r + 1][c] = true; 
			visited[r][c + 1] = true; 

			dfs(r, c + 1, result + getLeftTopPower(r, c));

			visited[r][c] = false; 
			visited[r + 1][c] = false; 
			visited[r][c + 1] = false; 
		}

		if(r - 1 >= 0 && c + 1 < M && !visited[r - 1][c] && !visited[r][c + 1]){
			visited[r][c] = true; 
			visited[r - 1][c] = true; 
			visited[r][c + 1] = true; 

			dfs(r, c + 1, result + getLeftBottomPower(r, c));

			visited[r][c] = false; 
			visited[r - 1][c] = false; 
			visited[r][c + 1] = false; 
		}
	}

	dfs(r, c + 1, result); 
}

int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> N >> M; 

	for(int i = 0; i < N; i++){
		for(int j = 0; j < M; j++){
			cin >> arr[i][j]; 
		}
	}

	// 부메랑을 만들 수 없는 경우 예외 처리 
	if(N == 1 || M == 1){
		ans = 0; 
	}else{
		dfs(0, 0, 0);
	}

	cout << ans; 
	
	return 0;
}