문제
https://www.acmicpc.net/problem/4781
풀이
각 테스트 케이스마다 사탕 n개의 칼로리와 가격이 주어질 때, m만큼의 돈으로 얻을 수 있는 최대 칼로리를 구하는 문제이다.
0/1 배낭 문제의 형태를 띄고 있지만, 각 사탕을 무제한으로 구매할 수 있고, 가격이 실수라는 점을 고려해야 한다. (0/1 배낭 문제에서는 각 물건이 1개씩만 존재한다고 가정하며, 배낭 용량이 정수로 주어진다.)
n, m 입력
int n, m;
double tmp;
cin >> n >> tmp;
m = (int)(tmp * 100 + 0.5); 상근이가 가진 돈의 양 m은 소수점 둘째 자리까지 주어지는 실수이다. 그러나, 실수로는 dp를 수행하기 어렵기 때문에 100을 곱해 정수로 변환하여 사용하자.
우리가 구하려는 값은 m만큼의 돈으로 얻을 수 있는 최대 칼로리이기 때문에, 배열을 이용하여 dp를 수행하기 위해 임의로 가격에 100을 곱해도 칼로리 값에는 영향을 미치지 않는다.
부동소수점 오차 고려
그리고 int로 형변환 하기 전에 0.5를 더해야 부동소수점 오차로 인해 잘못된 연산 결과가 나오는 것을 방지할 수 있다.
이 글을 읽어보면 다음과 같은 내용이 나온다.
부동 소수점 방식은 하나의 실수를 가수부와 지수부로 나누어 표현하는 방식이다.
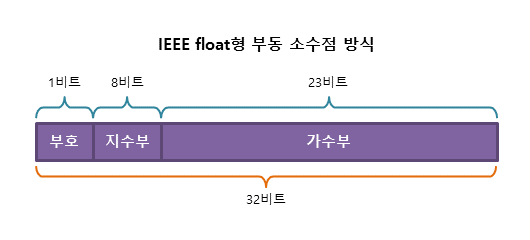
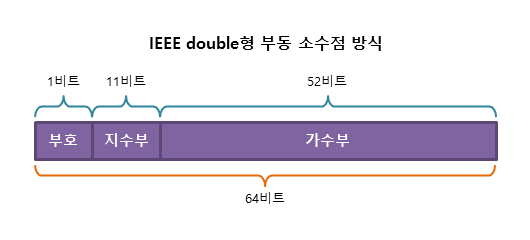
±(1.가수부) * 2^(지수부 - 127)
부동 소수점 방식에서의 오차는 위의 공식에 의해 발생한다. 이 공식을 사용하면 표현할 수 있는 범위는 늘어나지만, 10진수를 정확하게 표현할 수는 없게 된다.따라서 컴퓨터에서 실수를 표현하는 방법은 정확한 표현이 아닌 언제나 근사치를 표현할 뿐임을 항상 명심해야 한다.
double num = 0.1;
for(int i = 0; i < 1000; i++) {
num += 0.1;
}
System.out.print(num);
// 예상 출력: 100.1
// 실제 출력: 100.09999999999859따라서, 이 문제에서도 (소수점 둘째 자리까지 주어지는) 실수 타입의 가격에 단순히 100을 곱하고 int로 변환하면, 부동소수점 오차로 인한 잘못된 연산 결과가 나올 수 있다.
따라서, 100을 곱하고 0.5까지 더해줘야 int로 형변환 했을 때 우리가 원하는 값을 얻을 수 있을 것이다.
사탕 정보 입력
pair<int, int> candies[N_MAX];
for(int i = 0; i < n; i++){
cin >> candies[i].first >> tmp;
candies[i].second = (int)(tmp * 100 + 0.5);
}사탕의 가격을 입력 받을 때도 실수를 정수로 변환하여 pair에 저장하자.
dp 수행
int dp[M_MAX] = {0,};
for(int i = 0; i < n; i++){
int cal = candies[i].first;
int price = candies[i].second;
for(int j = price; j <= m; j++){
dp[j] = max(dp[j], dp[j - price] + cal);
}
}dp[i] : 돈을 i만큼 사용하여 얻을 수 있는 최대 칼로리 (i는 100을 곱해 정수로 변환한 상태)
dp[j]: 돈을 j만큼 사용하여 얻을 수 있는 최대 칼로리dp[j - price] + cal: 돈을 j보다 현재 사탕의 가격만큼 '덜' 썼을 때 얻는 최대 칼로리 + 현재 사탕의 칼로리
두 개 중에 최댓값으로 dp 배열을 갱신시키면서, 최종적으로 우리가 구하고자 하는 dp[m]을 얻는다.
C++ 코드
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
#include <cstring>
using namespace std;
const int N_MAX = 5001; // 물건 개수
const int M_MAX = 10001; // 상근이가 가진 돈 * 100
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
while(true){
int n, m;
double tmp;
cin >> n >> tmp;
m = (int)(tmp * 100 + 0.5);
if(n == 0 && m == 0) break;
pair<int, int> candies[N_MAX];
for(int i = 0; i < n; i++){
cin >> candies[i].first >> tmp;
candies[i].second = (int)(tmp * 100 + 0.5);
}
int dp[M_MAX] = {0,};
for(int i = 0; i < n; i++){
int cal = candies[i].first;
int price = candies[i].second;
for(int j = price; j <= m; j++){
dp[j] = max(dp[j], dp[j - price] + cal);
}
}
cout << dp[m] << "\n";
}
return 0;
}


