문제
https://www.acmicpc.net/problem/19951
2020년 5월 14일 논산훈련소에 입대한 태상이는 첫 총기 훈련에서 가스 조절기를 잃어버리는 중대한 실수를 범했다. 그로 인해, 태상이는 조교들에게 눈총을 받게 되었다. 조교들은 태상이에게 연병장(운동장)의 흙을 옮기는 일을 주고 제대로 수행하지 못하면 징계를 내리려고 한다.
연병장은 일렬로 이어진 N개의 칸으로 이루어져 있으며 각 칸마다 높이를 가지고 있고, 첫 번째 칸부터 순서대로 1번, 2번, 3번, ..., N번 칸으로 명칭이 붙어있다. 조교들은 총 M명이 있으며, 각 조교들은 태상이에게 a번 칸부터 b번 칸까지 높이 k만큼 흙을 덮거나 파내라고 지시한다. 흙은 주변 산에서 얼마든지 구할 수 있으므로 절대로 부족하지 않다.
태상이는 각 조교의 지시를 각각 수행하면, 다른 조교의 지시로 흙을 덮어둔 칸을 다시 파내기도 하는 비효율적인 일이 발생하는 것을 깨달았다. 그래서 태상이는 각 조교의 지시를 모아 연병장 각 칸의 최종 높이를 미리 구해 한 번에 일을 수행하려고 한다.
불쌍한 태상이를 위해 조교들의 지시를 모두 수행한 뒤 연병장 각 칸의 높이를 구하자.
입력
첫 줄에 연병장의 크기 N과 조교의 수 M이 주어진다.
둘째 줄에 연병장 각 칸의 높이 Hi가 순서대로 N개 주어진다.
셋째 줄부터 M개의 줄에 각 조교의 지시가 주어진다.
각 조교의 지시는 세 개의 정수 a, b, k로 이루어져 있다.
- k ≥ 0인 경우 a번 칸부터 b번 칸까지 높이가 각각 |k| 만큼 늘어나도록 흙을 덮어야 한다.
- k < 0인 경우 a번 칸부터 b번 칸까지 높이가 각각 |k| 만큼 줄어들도록 흙을 파내야 한다.
출력
모든 지시를 수행한 뒤 연병장 각 칸의 높이를 공백을 사이에 두고 출력한다.
제한
- 1 ≤ N ≤ 100,000
- 1 ≤ M ≤ 100,000
- -10,000 ≤ Hi ≤ 10,000
- N, M, Hi는 정수
- 조교의 지시: 1 ≤ a ≤ b ≤ N, |k| ≤ 100
예제
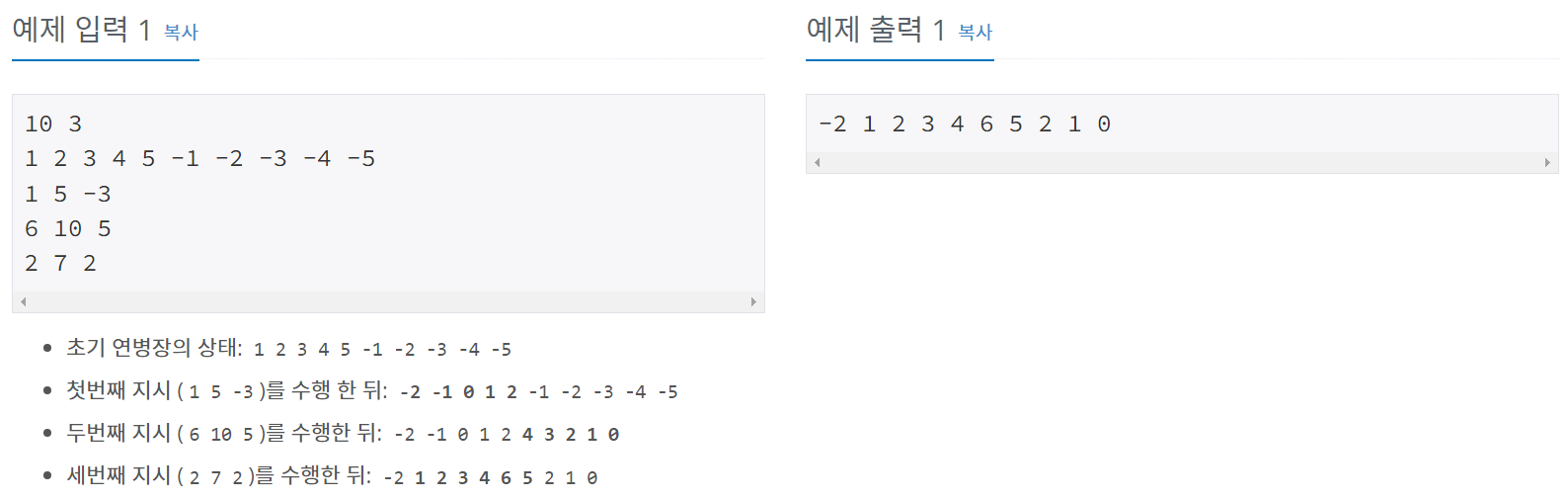
풀이
시간 초과: O(nm)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n, m; // 최대 10만
cin >> n >> m; // 연병장의 크기, 조교의 수
vector<int> h(n + 1); // 각 칸의 높이
for(int i = 1; i <= n; i++){
cin >> h[i]; // 절댓값으로 최대 1만
}
// 시간복잡도: O(nm)
for(int i = 0; i < m; i++){
int a, b, k;
cin >> a >> b >> k;
// 구간 a부터 b까지 각 칸의 높이 +/-|k|
for(int j = a; j <= b; j++){ // 최악의 경우 n
if(k >= 0){
h[j] += k;
}else{ // 절댓값만큼 파내기
h[j] -= -k;
}
}
}
for(int i = 1; i <= n; i++){
cout << h[i] << " ";
}
cout << endl;
return 0;
}이렇게 해결했을 때, 큰 문제가 한 가지 있다. 최악의 경우를 생각해보자.
연병장의 크기 N이 최댓값인 100,000 이고, 조교의 수 M이 최댓값인 100,000 이고, 모든 100,000명의 조교가 내리는 지시가 모두 동일하게 [ 1 , 100000 , 1 ] 인 경우를 생각해보자.
즉, 100,000 명의 모든 조교가 "연병장의 1번칸부터 마지막 칸(100000번 칸) 까지 높이가 1만큼 늘어나도록 흙을 덮어!" 라고 지시를 한 것이다. 이 때, 위에서 이야기했던 간단한 접근 방법으로 계산을 하게 되면 다음과 같이 계산이 될 것이다.
연병장의 크기인 100,000 칸을 100,000번 방문해야 하기 때문에 총 100,000 * 100,000 만큼의 연산을 하게 된다. 그럼 10,000,000,000 만큼의 연산을 하게 된다. 말도 안되게 시간이 오래 걸린다는 것이다. 그래서 이 문제를 이와같이 매우 간단한 접근 방법으로 해결을 할 수는 없다.
누적 합: O(n)
https://yabmoons.tistory.com/729
그래서 이 문제를 "누적합" 을 이용한 방법으로 해결해 볼 것이다. 다음과 같은 배열이 있다고 생각해보자.
[ 1 , 2 , 3 , 4 , 5 ]
이때, "1번 칸부터 3번칸까지 +2 만큼 하세요" 라고 한다면, 저 배열에서 바로 계산을 하는게 아니라, 새로운 배열에서 계산을 해줄 것이다. 그러기 위해서 먼저 모든 값이 0으로 초기화 되어 있는 새로운 배열을 하나 선언해보자.
[ 0 , 0 , 0 , 0 , 0 ]
그리고 "1번 칸부터 3번칸까지 +2 만큼 하세요" 라는 명령을 수행하기 위해서 다음과 같이 연산을 진행해줄 것이다.
[ 2 , 0 , 0 , -2 , 0 ]
1번 칸에는 + 2를, 4번 칸에는 -2를 시켜준 것이다. 왜 갑자기 이런 계산을 했을까?!
그 전에, 위의 상태에서 이 배열에서 앞에서부터의 누적값을 한번 구해보자. 구해보면 다음과 같을 것이다.
[ 2 , 2 , 2 , 0 , 0 ]
첫 번째 칸 = 이전의 칸이 없으므로 '2' 그대로 유지.
두 번째 칸 = 이전 칸 까지의 총합이 '2'였고, 두 번째 칸의 값이 '0'이였으므로 2 + 0 = '2'
세 번째 칸 = 이전 칸 까지의 총합이 '2'였고, 세 번째 칸의 값이 '0'이였으므로 2 + 0 = '2'
네 번째 칸 = 이전 칸 까지의 총합이 '2'였고, 네 번째 칸의 값이 '-2' 였으므로 2 + (-2) = '0'
다섯번째 칸 = 이전 칸 까지의 총합이 '0' 이였고, 다섯 번째 칸의 값이 '0'이였으므로 '0'.
위와 같이 계산된다. 그리고 원본의 배열인 [ 1 , 2 , 3 , 4 , 5 ] 와 [ 2 , 2 , 2 , 0 , 0 ]을 더하게 되면
[ 3 , 4 , 5 , 4 , 5 ] 와 같이 우리가 원했던 1번칸 ~ 3번 칸만 +2가 된 결과를 얻을 수 있다.
즉 ! "A번째 칸부터 B번째 칸까지 +a를 하세요" 라고 한다면, 우리는 새로운 배열에서
"A번째 칸에 +a를, (B+1)번째 칸에 -a"를 한 뒤에, 이 배열에서의 누적합을 구하고, 원본 배열과 합쳐주기만 한다면 우리가 원하는 결과를 구할 수 있다.
이 방법을 이용하면 몇개의 명령어(m)가 몇개의 범위(n)에 대해 주어지더라도,
A번째 칸에 +a, (B+1)번째 칸에 -a를 하고, 이에 대한 누적합을 구하기 위해 N번, 그리고 원본 배열과 합치기 위해 N번 탐색을 진행하면, 시간초과 없이 문제를 해결할 수 있다!
#include <iostream>
#include <vector>
#include <algorithm>
#define MAX 100'001
using namespace std;
struct cmd {
int a;
int b;
int k;
};
int n, m;
int arr[MAX];
int accSum[MAX];
cmd cmdArr[MAX];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for(int i = 0; i < n; i++){
cin >> arr[i];
}
for(int i = 0; i < m; i++){
int a, b, k;
cin >> a >> b >> k;
cmdArr[i] = { a - 1, b - 1, k };
}
for(int i = 0; i < m; i++){
int start = cmdArr[i].a;
int end = cmdArr[i].b;
int k = cmdArr[i].k;
// start에 +k, (end+1)에 -k
accSum[start] += k;
accSum[end + 1] -= k;
}
// accSum 배열의 누적합 구하기
for(int i = 0; i < n; i++){
accSum[i + 1] += accSum[i];
}
// 누적합 배열과 원본 배열 더하기
for(int i = 0; i < n; i++){
arr[i] += accSum[i];
cout << arr[i] << " ";
}
cout << endl;
return 0;
}

