[백준] 11660번. 구간 합 구하기 5

leeeha·2022년 7월 4일

백준

목록 보기

40/185

문제

https://www.acmicpc.net/problem/11660

풀이

시간 초과: O( $n^2 m$ )

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int arr[1025][1025]; // n은 최대 1024

int main()
{
	ios::sync_with_stdio(0);
    cin.tie(0);

	int n, m; 
	cin >> n >> m; // m은 최대 10만 

	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){ 
			int val; 
			cin >> val; 
			arr[i][j] = val; 
		}
	}

	while(m--){ // 최대 10만 
		int x1, y1, x2, y2;
		cin >> x1 >> y1 >> x2 >> y2;

		// 최악의 경우 시간복잡도: O(n^2)
		int sum = 0; 
		for(int r = x1; r <= x2; r++){ 
			for(int c = y1; c <= y2; c++){ 
				sum += arr[r][c]; 
			}
		}
		cout << sum << "\n";
	}
	
	return 0;
}

단순하게 이중 반복문을 사용하니까 시간초과가 떴다,, 더 효과적으로 누적 합을 구할 수 있는 방법이 뭘까! 고민해도 도저히 답을 모르겠어서 구글링을 했다..!

DP

DP 적용 단계

https://velog.io/@jxlhe46/알고리즘-다이나믹-프로그래밍

문제의 특성을 분석하여 최적성의 원리가 성립되는지 (큰 문제를 작은 문제로 나눌 수 있으며, 작은 문제의 답을 모아서 큰 문제를 해결할 수 있는지) 확인한다.
주어진 문제에 대해 최적해를 제공하는 '점화식'을 도출한다.
가장 작은 부분 문제부터 점화식의 해를 구한 뒤 이를 테이블에 저장한다.
테이블에 저장되어 있는 부분 문제의 해를 이용하여 점차적으로 입력 크기가 큰 상위 문제의 해를 구한다. (상향식)

https://donggoolosori.github.io/2020/10/13/boj-11660/

이 문제에서 누적 합을 효과적으로 구하려면, dp 테이블에 이미 계산된 결과를 저장해두고 필요에 따라 그 값을 재사용 하면 된다. 먼저, 이 문제의 최적해를 구하기 위한 점화식을 도출해보자.

dp[i][j] = dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1] + arr[i][j];

위의 식에서 arr는 2차원 상에서 각 원소의 값을 저장하는 배열이고, dp는 그 원소들의 누적합을 저장하는 배열이다. 위 점화식이 어떻게 유도된 것인지 예시를 통해 이해해보자!

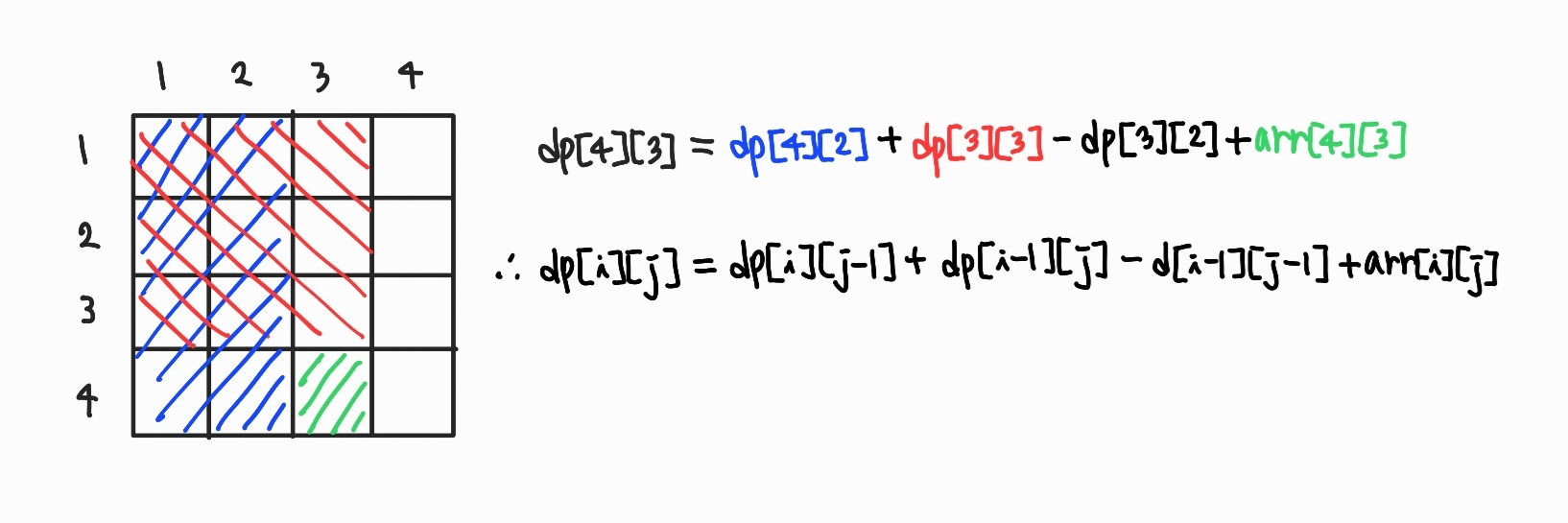
위의 그림을 보면 바로 이해할 수 있을 것이다. dp[4][3]을 구하려면, dp[4][2]와 dp[3][3]를 먼저 더하고, 거기서 중복되는 부분은 빼준 뒤에, 마지막으로 해당 위치의 원소 값을 더해주면 된다.

그렇다면, (x1, y1)부터 (x2, y2)까지의 구간 합을 구하려면 어떻게 해야 할까? 위의 점화식과 같은 원리를 적용하면 된다.

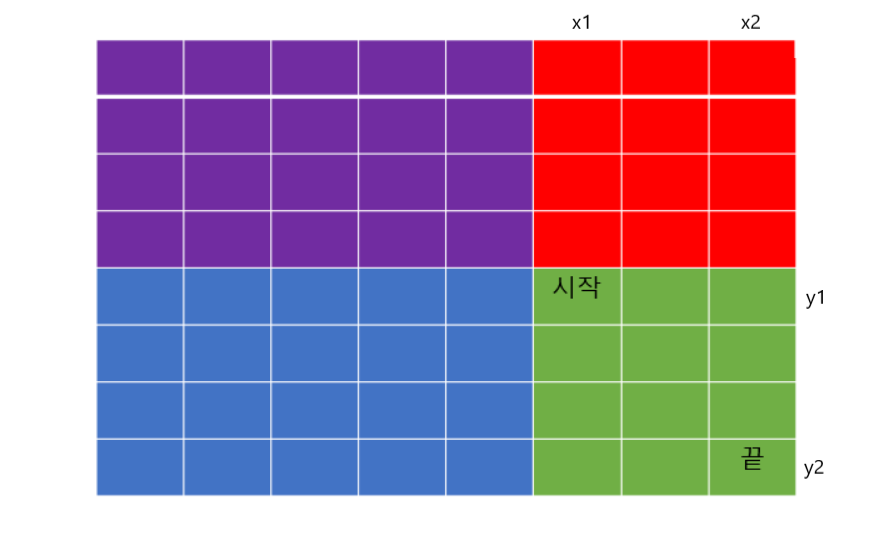
(x1, y1) ~ (x2, y2) 구간 합 = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]

dp[x2][y2]는 전체 영역의 누적 합이다.
dp[x1 - 1][y2]는 파란색 영역과 보라색 영역을 합친 값이므로, 1번에서 빼준다.
dp[x2][y1 - 1]은 빨간색 영역과 보라색 영역을 합친 값이므로, 1번에서 빼준다.
dp[x1 - 1][y1 - 1]은 보라색 영역의 값인데, 2번과 3번에서 중복해서 빼주기 때문에 한번 더해준다.

답안

#include <iostream>
#define MAX 1025 // n은 최대 1024
using namespace std;

int arr[MAX][MAX]; 
int dp[MAX][MAX];

int main()
{
	ios::sync_with_stdio(0);
    cin.tie(0);

	int n, m; 
	cin >> n >> m; // m은 최대 10만 

	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){ 
			cin >> arr[i][j]; 
			dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i-1][j-1] + arr[i][j];
		}
	}

	int x1, y1, x2, y2;
	int ans = 0;
	
	while(m--){
		cin >> x1 >> y1 >> x2 >> y2;

		ans = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];
		cout << ans << "\n";
	}
	
	return 0;
}