문제
https://www.acmicpc.net/problem/2981
트럭을 타고 이동하던 상근이는 경찰의 검문을 받게 되었다. 경찰은 상근이가 운반하던 화물을 하나하나 모두 확인할 것이기 때문에, 검문하는데 엄청나게 오랜 시간이 걸린다.
상근이는 시간을 때우기 위해서 수학 게임을 하기로 했다.
먼저 근처에 보이는 숫자 N개를 종이에 적는다. 그 다음, 종이에 적은 수를 M으로 나누었을 때, 나머지가 모두 같게 되는 M을 모두 찾으려고 한다. M은 1보다 커야 한다.
N개의 수가 주어졌을 때, 가능한 M을 모두 찾는 프로그램을 작성하시오.
입력
첫째 줄에 종이에 적은 수의 개수 N이 주어진다. (2 ≤ N ≤ 100)
다음 줄부터 N개 줄에는 종이에 적은 수가 하나씩 주어진다. 이 수는 모두 1보다 크거나 같고, 1,000,000,000보다 작거나 같은 자연수이다. 같은 수가 두 번 이상 주어지지 않는다.
항상 M이 하나 이상 존재하는 경우만 입력으로 주어진다.
출력
첫째 줄에 가능한 M을 공백으로 구분하여 모두 출력한다. 이때, M은 증가하는 순서이어야 한다.
예제
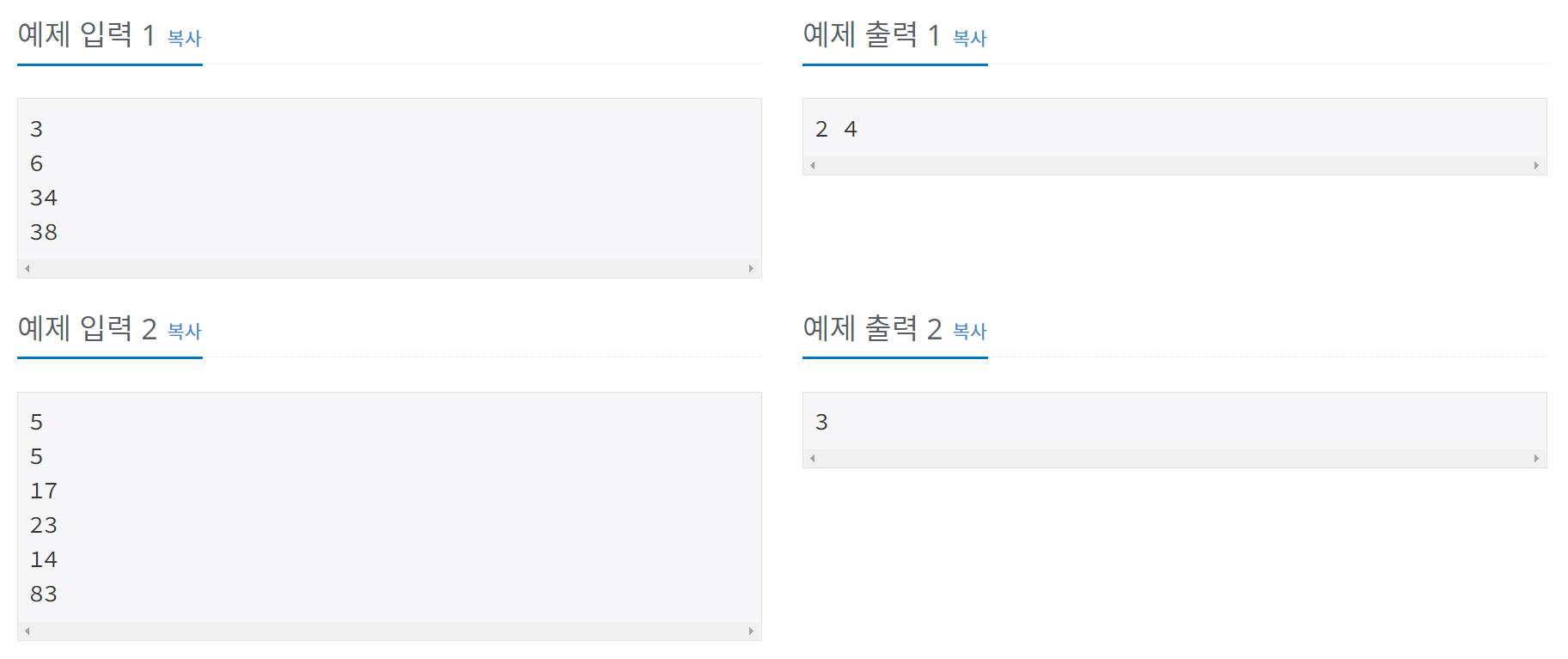
풀이과정
시간초과
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
vector<int> v;
for(int i = 0; i < n; i++){
int val;
cin >> val;
v.push_back(val);
}
int max = *max_element(v.begin(), v.end());
for(int i = 2; i < max; i++){ // 최대 10억,,,,
// 첫번째 원소에 대한 나머지 먼저 구하기
int temp = v[0] % i;
int j;
for(j = 1; j < v.size(); j++){
// 한번이라도 이전과 다른 나머지 값이 나오면
if(temp != v[j] % i){
break; // 바로 그 다음 i로 이동!!
}else{
temp = v[j] % i; // 나머지 값 업데이트
}
}
// 모든 벡터 원소에 대해 나머지 값이 동일하면
if(j == v.size()){
// 그때의 i 값 출력
cout << i << " ";
}
}
return 0;
}다른 풀이 참고
https://kjwan4435.tistory.com/59
이 문제는 브루트포스로 모든 가능한 수를 탐색하면 시간 초과가 난다. 그렇다면 이 문제를 어떻게 풀어야 할까?
어떤 수 A, B, C가 있고 이들을 K로 나눈 나머지가 항상 D야! 라는 말을 다시 생각해보면
(A-D), (B-D), (C-D)를 K로 나눈 나머지는 항상 0이야! 라는 말이 된다.
이게 이 문제의 핵심이다! 결국 우리가 구하려고 하는 K는 (A-D), (B-D), (C-D)의 공약수가 된다는 것이다. 그리고 이 공약수는, (A-D), (B-D), (C-D)의 최대공약수의 약수가 될 것이다.
그러면 여기서 어떤 두 수 A와 B의 최대공약수는 어떻게 구할 수 있을까? 우선 다음 문장을 먼저 이해해보자!
만약 A가 B로 나누어 떨어지지 않는다면, A와 B의 최대공약수는 A-B와 B의 최대공약수와 같다.
예를 들어, A와 B의 최대공약수를 c라고 해보자. 그러면 A는 a*c, B는 b*c로 나타낼 수 있고, 우리는 최대공약수 c를 찾기 위해 그 계수인 a와 b의 값을 계속 줄여나갈 것이다. 그리고 (a-b)*c와 b*c도 마찬가지로 c의 배수이기 때문에, 결국 A와 B의 최대공약수는 A-B와 B의 최대공약수와 같다고 말할 수 있다. 따라서 A와 B의 계수를 줄여나가며 최종적으로 최대공약수 c가 출력되도록 하는 재귀함수를 정의할 수 있다.
그럼 여기서 그치지 말고 한 스텝 더 나아가서, 이런 생각을 해볼 수 있다.
A, B, C, ... , Z까지의 최대공약수를 빠르게 구하기 위해서, (A-B), (B-C), ... , (Y-Z)의 최대공약수를 구하는 것이다! 그 이유는, 간격이 좁은 두 수가 있다면 재귀 호출의 깊이를 줄일 수 있기 때문이다. 결국 이 문제는 인접한 두 수의 차이의 최대공약수를 구하는 문제로 바뀌었다! 이렇게 최대공약수를 먼저 구하고, 그 수의 약수를 구하면 최종 답을 구할 수 있을 것이다.
최대공약수 계산 방법 (유클리드 호제법)
👉 https://velog.io/@jxlhe46/알고리즘-재귀-함수#최대공약수-계산-예제
곱셈에 대칭인 약수의 성질
👉 https://velog.io/@jxlhe46/알고리즘-소수-판별#약수의-성질
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
int GCD(int a, int b){
if(a % b == 0){
return b;
}else{
return GCD(b, a % b);
}
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
vector<int> v;
v.resize(n);
for(int i = 0; i < n; i++){
cin >> v[i];
}
// 연속된 값의 차를 최소화 하기 위해 정렬
sort(v.begin(), v.end());
int gcd = v[1] - v[0];
for(int i = 2; i < n; i++) {
// 인접한 두 수의 차이의 최대공약수 먼저 구하기
gcd = GCD(gcd, v[i] - v[i - 1]);
}
// 위에서 구한 최대공약수의 약수 구하기
vector<int> divisor;
for(int i = 1; i <= gcd; i++){
if(gcd % i == 0){
// 약수의 성질에 의해 중간까지만 확인하면 됨.
if(i > gcd / i) break;
divisor.push_back(i);
if(i == gcd / i) break; // 제곱근이면 하나만 뽑고 멈추기
// 약수는 곱셈에 대해 대칭이니까
divisor.push_back(gcd / i);
}
}
// 오름차순 정렬
sort(divisor.begin(), divisor.end());
// 첫번째 원소인 1은 제외하고 출력
for(int i = 1; i < divisor.size(); i++){
cout << divisor[i] << " ";
}
return 0;
}


