문제

https://www.acmicpc.net/problem/9095

n은 1 이상 10 이하의 정수이며, 1, 2, 3을 사용해서 n을 만들 수 있는 모든 경우의 수를 구하는 문제이다.

풀이

처음에는 있는 그대로 문제를 풀려고 해봤다. 1, 2, 3으로 가능한 모든 조합이

1
2
3
1 2
1 3
2 3
1 2 3

이 7가지이고, 이 조합을 사용해서 n을 만들 수 있는 모든 경우의 수를 순열로 구해볼까..? 라고 생각했다. 예를 들어 n이 7이면, 다음과 같은 경우의 수를 생각할 수 있다.

1 1 1 1 1 1 1 → 1
2 2 2 1 → 4
2 2 1 1 1 → 10
2 1 1 1 1 1 → 6
3 3 1 → 3
3 1 1 1 1 → 5
3 2 2 → 3
3 2 1 1 → 12

총 44가지가 나온다. 각 경우의 수는 같은 것이 있는 순열로 구했다. 그런데 이걸 도대체 어떻게 코딩으로 구현해야 할지 감이 오질 않았다. 그래서 결국 다른 사람의 풀이를 참고했다.

백트래킹

DFS, 백트래킹을 이용하여 중복 순열을 구현할 수 있다.

문제에서는 가짓수만 구하라고 했지만, 재귀함수의 작동 원리를 이해하기 위해 선택된 숫자가 무엇인지 출력하는 부분도 구현해보았다.

#include <iostream> 
#include <vector> 
#include <string>
#include <algorithm> 
#include <queue> 
#include <cstring> 
using namespace std;

int t, n;
int answer = 0;
vector<int> selected; 

void printSelectedElements() {
	for(int e: selected){
		cout << e << " ";
	}
	cout << endl;
}

void dfs(int sum){
	// 1 or 2 or 3을 더해서 n이 되면 결과 처리 후 
	// 더 이상 깊이 들어가지 않고 다음 경우의 수 탐색 (가지치기) 
	if(sum == n){
		answer++;
		printSelectedElements();
		return;
	}

	if(sum > n) return;

	// 중복 순열 (인덱스가 1부터 시작) 
	for(int i = 1; i <= 3; i++){ 
		selected.push_back(i); 
		dfs(sum + i); 
		selected.pop_back(); 
	}
}

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	// cin >> t; 

	// while(t--){
		cin >> n;
		
		dfs(0);
		cout << answer << endl; 
		answer = 0; 
	// }
	
	
	return 0;
}

printSelectedElements 함수에서 합이 n이 되는 숫자들을 출력할 때는, 그 숫자들의 개수가 매번 달라지기 때문에 벡터에 push, pop 하는 식으로 선택된 원소들을 저장하고 출력했다.

n이 4일 때 다음과 같은 결과가 나오는데, 그림을 직접 그려보면 재귀 함수의 작동 원리를 이해할 수 있다.

1 1 1 1
1 1 2
1 2 1
1 3
2 1 1
2 2
3 1

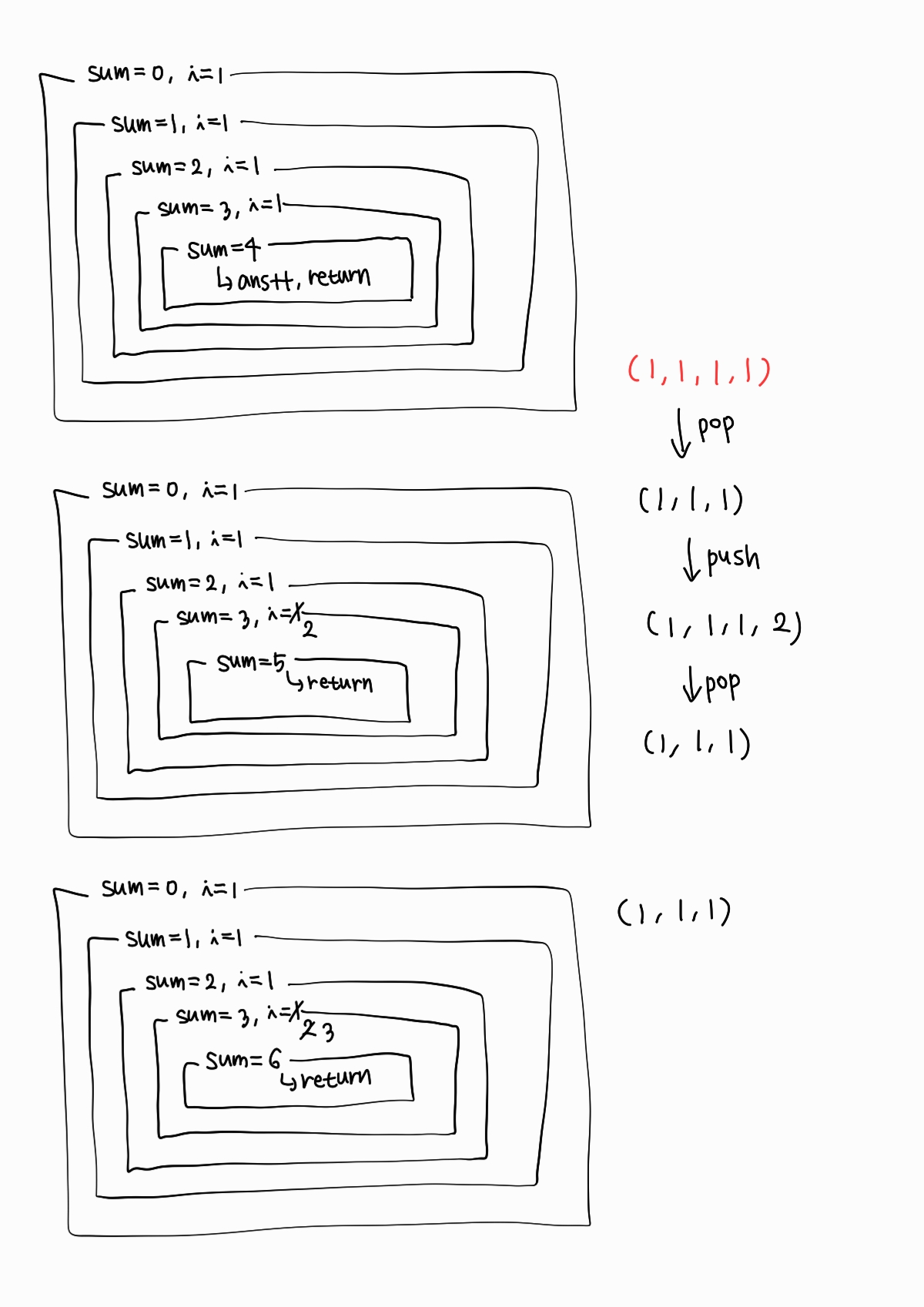
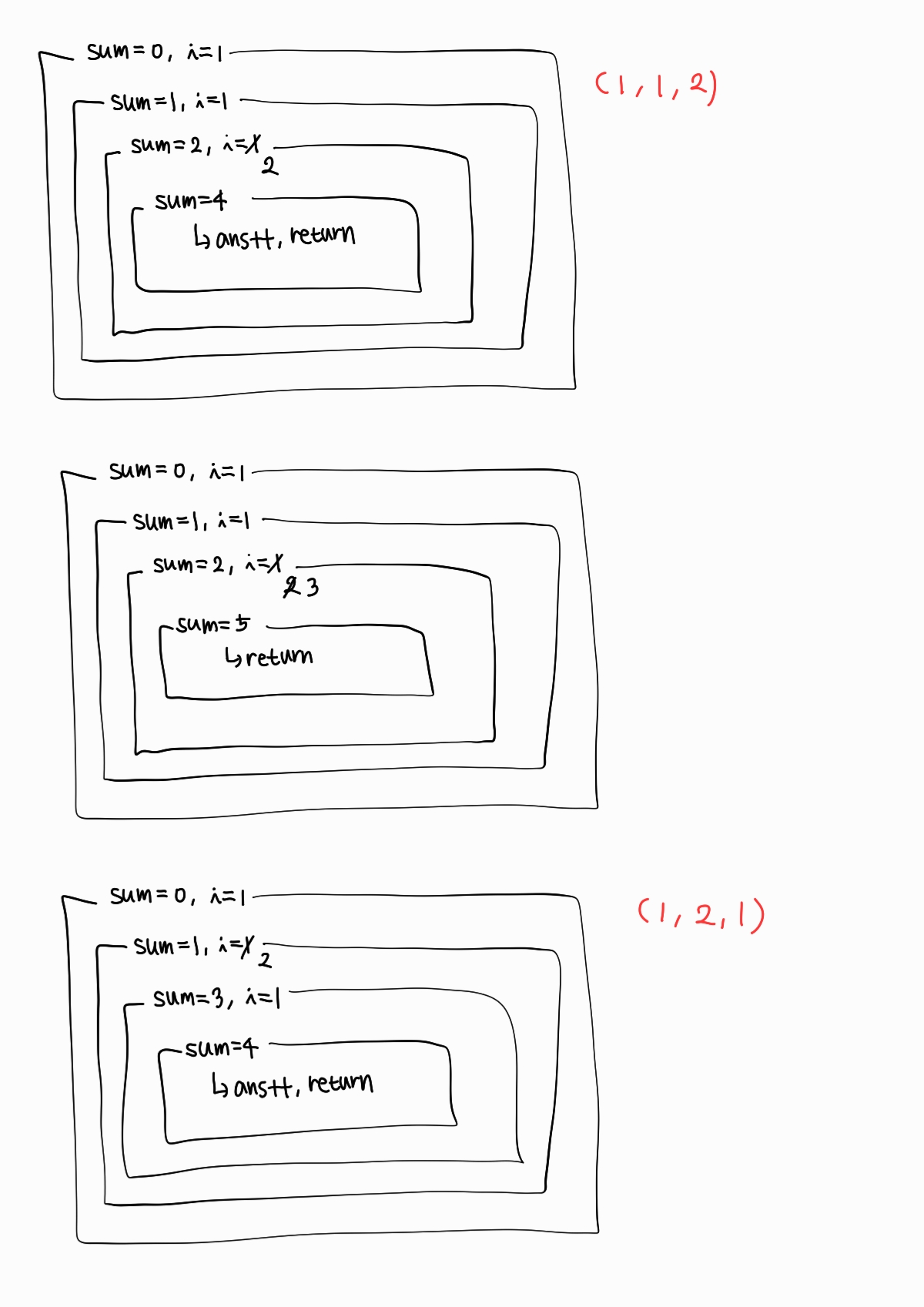
이런 식으로 1, 2, 3이라는 숫자 중에 중복을 허용하여 n을 만드는 모든 경우의 수를 구할 수 있다. (순서를 고려하므로 중복 순열)

답안 제출에 필요한 코드만 요약하면 다음과 같다.

#include <iostream> 
#include <vector> 
#include <string>
#include <algorithm>
using namespace std;

int t, n;
int answer = 0;

void dfs(int sum){
	// 1 or 2 or 3을 더해서 n이 되면 결과 처리 후 
	// 더 이상 깊이 들어가지 않고 다음 경우의 수 탐색
	if(sum == n){
		answer++;
		return;
	}

	if(sum > n) return;

	// 중복 순열 (인덱스 1부터 시작)
	for(int i = 1; i <= 3; i++){ 
		dfs(sum + i); 
	}
}

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	cin >> t; 

	while(t--){
		cin >> n;
		
		dfs(0);
		cout << answer << endl;
		answer = 0; 
	}
	
	return 0;
}

DP

n번째 칸에 도달하는 방법은 총 3가지로 분류할 수 있다.

• (n-1) 칸에서 1칸 뛰어서 도달하는 경우
• (n-2) 칸에서 2칸 뛰어서 도달하는 경우
• (n-3) 칸에서 3칸 뛰어서 도달하는 경우

따라서, 다음과 같이 점화식을 세우고 dp로 해결할 수 있다.

dp[n] = dp[n - 1] + dp[n - 2] + dp[n - 3]

실제로 경우의 수를 하나씩 따져보면 위와 같은 점화식이 성립한다는 걸 확인할 수 있다.

#include <iostream> 
#include <vector> 
#include <string>
#include <algorithm>
using namespace std;

const int MAX = 11; 
int dp[MAX];
int t, n;

int main() {
	ios::sync_with_stdio(0);
    cin.tie(0);

	dp[1] = 1; 
	dp[2] = 2; 
	dp[3] = 4; 

	cin >> t;

	while(t--){
		cin >> n;
		
		for(int i = 4; i <= n; i++){
			dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];
		}

		cout << dp[n] << endl; 
	}
	
	return 0;
}