[알고리즘] 재귀 함수 (Recursive Function)

참고 자료: https://youtu.be/gFpKGWdEE5g

재귀 함수 (Recursive function)이란 자기 자신을 다시 호출하는 함수이다.

종료 조건 없는 경우

가장 단순한 형태의 재귀 함수는 다음과 같다. '재귀 함수를 호출합니다.'라는 문자열을 계속 출력하다가 최대 재귀 깊이를 초과하면 에러 문구가 출력된다.

def recursive_function():
	print('재귀 함수를 호출합니다.')
    recursive_function()

recursive_function()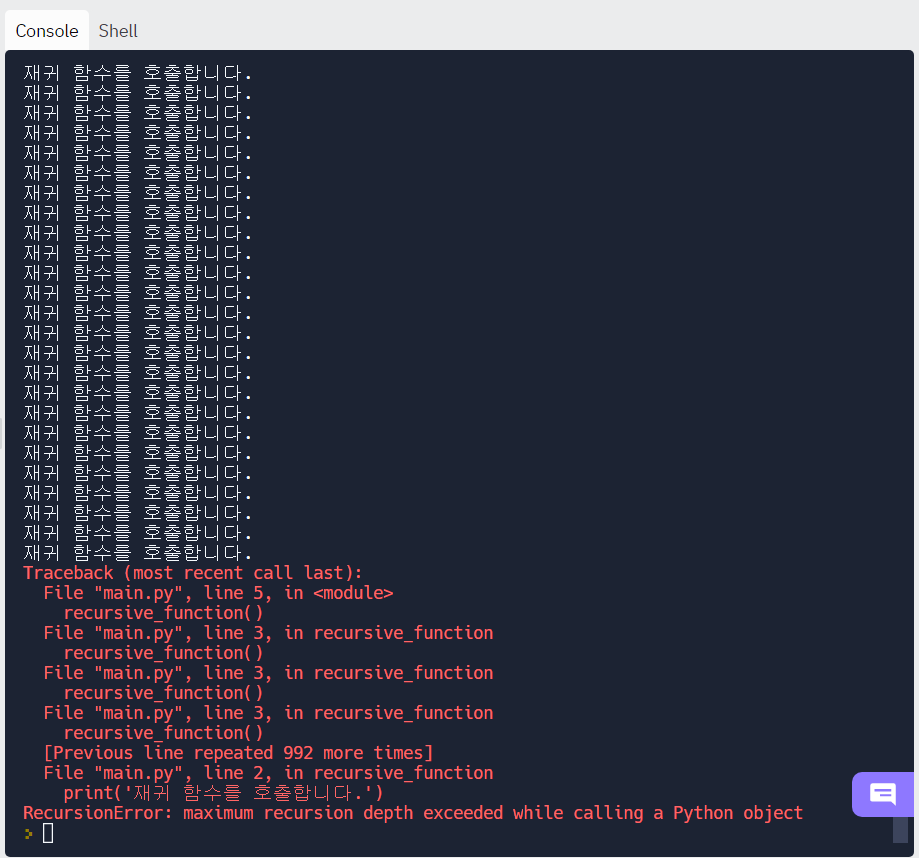

재귀 함수가 호출될 때마다 컴퓨터 메모리의 스택 프레임에 관련 리소스가 계속 쌓이게 되는데, 무한히 호출을 반복하면 스택 오버플로우가 발생하여 에러 문구가 출력된다.

종료 조건 있는 경우

일반적으로 재귀 함수를 문제 풀이에서 사용할 때는 재귀 함수의 종료 조건을 반드시 명시해야 한다. 그렇지 않으면 위의 예시처럼 함수가 무한히 호출될 수 있다.

def recursive_function(i):
	# 100번째 호출했을 때 종료되도록 종료 조건 명시
    if i == 100:
    	return
        
    print(i, '번째 재귀함수에서', i + 1, '번째 재귀함수를 호출합니다.')
    recursive_function(i + 1)
    
    print(i, '번째 재귀함수를 종료합니다.')
    
    
recursive_function(1)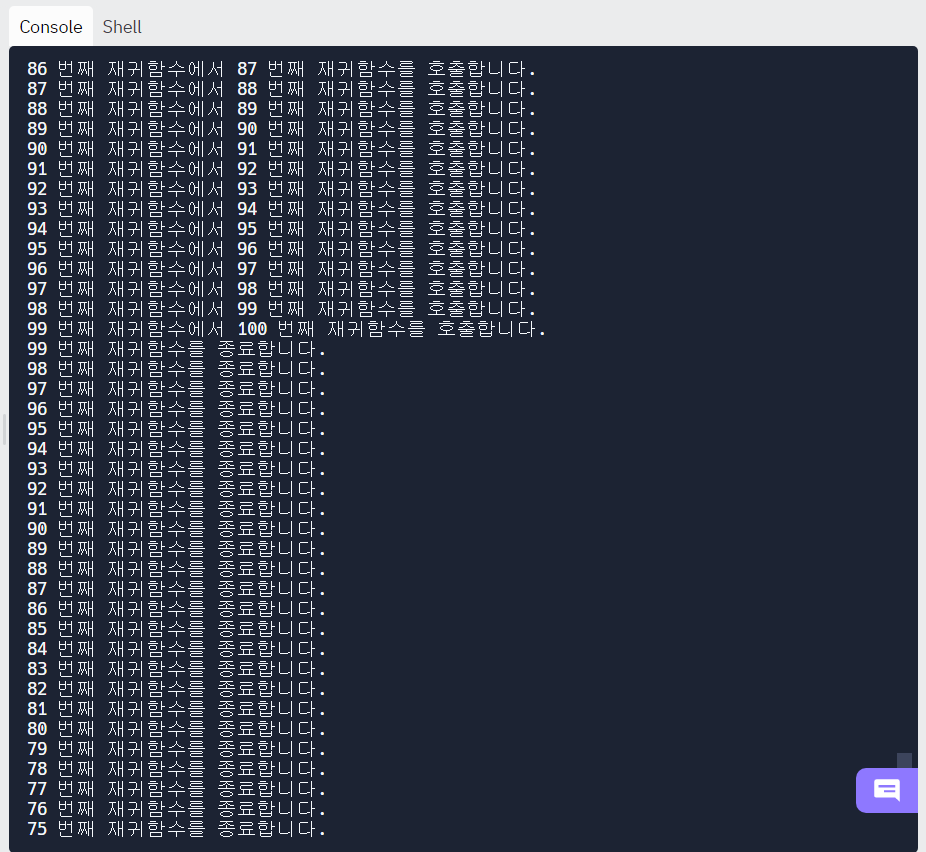

이처럼 재귀 함수를 이용하면 스택에 데이터를 넣었다가 꺼내는 것과 마찬가지로, 각각의 함수에 대한 정보가 스택 프레임에 담기면서 차례대로 호출되고, 가장 마지막에 호출된 함수부터 차례로 종료된다. (Last In First Out, LIFO)

팩토리얼 구현 예제

# 반복적으로 구현한 n! 
def factorial_iterative(n):
	result = 1 
	# 1부터 n까지의 수를 차례로 곱하기
	for i in range(1, n + 1):
		result *= i
	return result

# 재귀적으로 구현한 n!
def factorial_recursive(n):
	if n <= 1:
		return 1
	# n! = n * (n - 1)!을 그대로 코드로 작성하기
	return n * factorial_recursive(n - 1)

print('반복적으로 구현: ', factorial_iterative(5)) // 120
print('반복적으로 구현: ', factorial_recursive(5)) // 120

최대공약수 계산 예제

두 개의 자연수에 대한 최대공약수 (Greatest Common Divisor, GCD)를 계산하는 대표적인 알고리즘으로는 유클리드 호제법이 있다.

• 두 자연수 A, B에 대하여 (A > B) A를 B로 나눈 나머지를 R이라고 했을 때,
• A와 B의 최대공약수는 B와 R의 최대공약수와 같다.

예를 들어 192와 162의 최대공약수를 다음과 같이 구할 수 있다.

단계	A	B	R
1	192	162	30
2	162	30	12
3	30	12	6
3	12	6	0

GCD(192, 162) = GCD(12, 6) = 6

위와 같은 유클리드 호제법의 아이디어를 그대로 재귀 함수로 작성할 수 있다.

# a가 b로 나누어 떨어질 때까지 재귀 호출을 반복한다. 
def gcd(a, b):
	if a % b == 0:
		return b
	else:
		return gcd(b, a % b)

print(gcd(192, 162)) // 6

재귀 함수 사용 시 유의사항

• 재귀 함수를 잘 활용하면 복잡한 알고리즘을 간결하게 작성할 수 있다. (단, 오히려 다른 사람이 이해하기 어려운 형태의 코드가 될 수도 있으므로 신중하게 사용해야 한다.)
• 모든 재귀 함수는 반복문을 이용하여 동일한 기능을 구현할 수 있는데, 재귀 함수가 반복문보다 유리할 때도 있고 불리할 때도 있다.
• 컴퓨터가 함수를 연속적으로 호출하면, 컴퓨터 메모리 내부의 스택 프레임에 쌓인다. 그래서 스택 자료구조를 사용해야 할 때 구현상 스택 라이브러리 대신 재귀 함수를 이용하는 경우가 많다.