비교적 구현 방법이 쉬운 버블 정렬, 선택 정렬, 삽입 정렬은 평균 시간복잡도가 O(N^2)이다. 이 글에서는 평균 시간복잡도가 O(NlogN)인 합병 정렬, 퀵 정렬에 대해 알아볼 것이다. 그리고 추가적으로 알아두면 좋은 카운팅 정렬까지 다뤄볼 예정이다.
합병 정렬 (Merge Sort)
머지 소트는 재귀적으로 배열을 분할하여 정렬한 다음 이를 다시 합치는 방법이다.
이 알고리즘은 최악의 경우에도 O(NlogN)의 시간복잡도를 보장한다. N이 10만 정도라고 할 때, O(N^2)은 컴퓨터 성능에 따라 10초에서 1분 정도의 시간이 걸린다. 그런데 O(NlogN) 알고리즘은 눈 감았다 뜨기도 전에 이미 연산이 다 끝나는 속도이다. N이 커질수록 이 격차는 더 커질 것이다!
머지 소트를 위해서는 먼저 길이가 N, M인 두 정렬된 배열을 합쳐서 길이가 N+M인 배열을 만드는 방법을 알아야 한다.
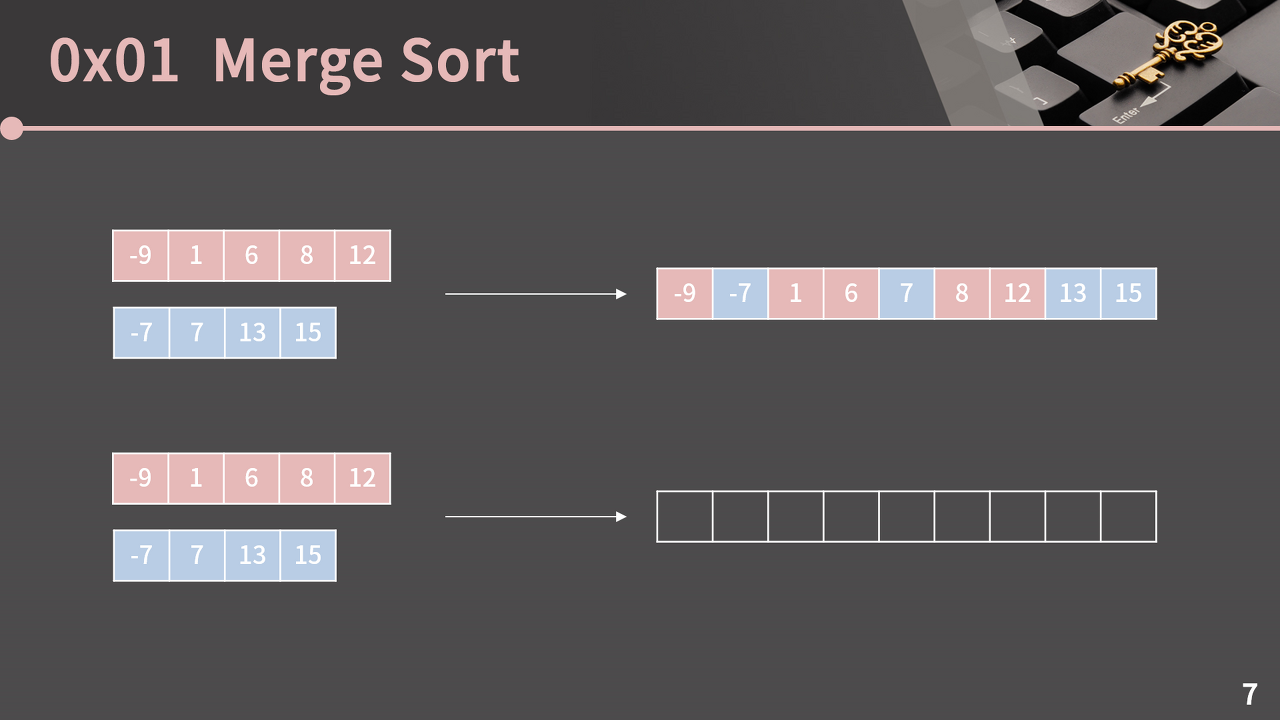
제일 처음에는 첫번째 원소끼리 값을 비교해서 더 작은 값을 새로운 배열의 첫번째 원소로 저장하면 된다.
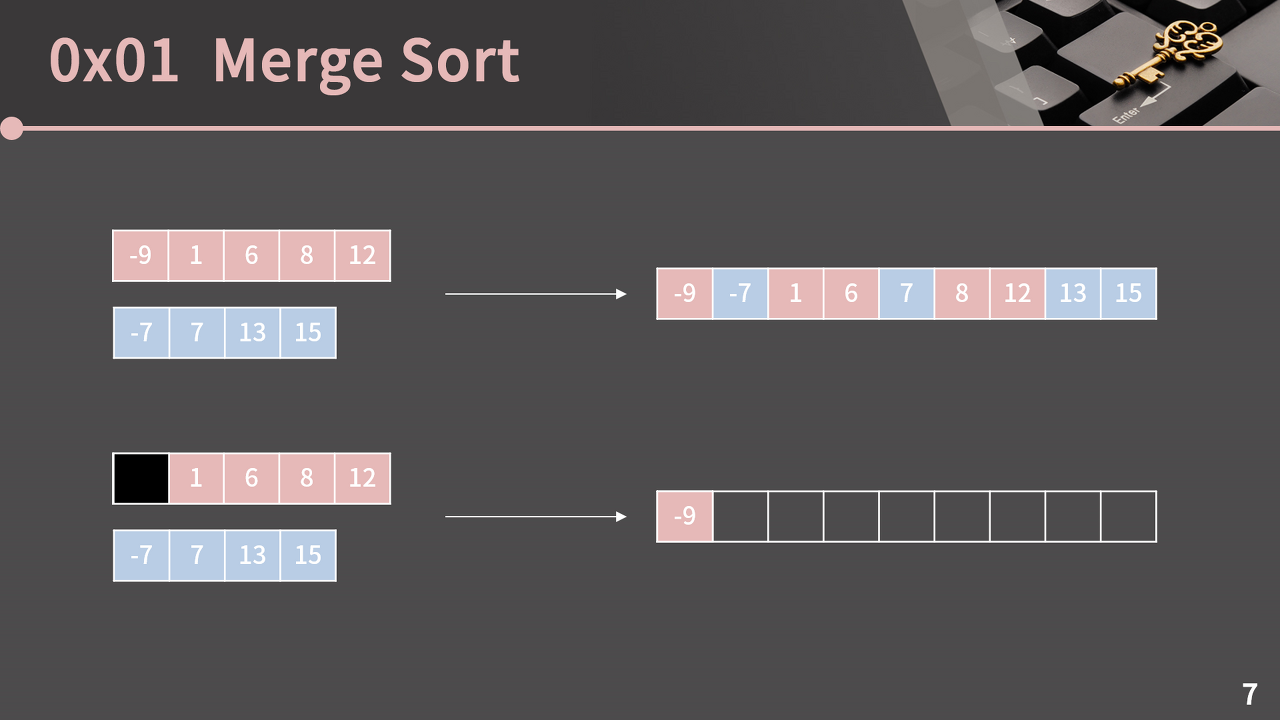
그 다음에는 1과 -7을 비교하여 더 작은 -7을 저장한다.
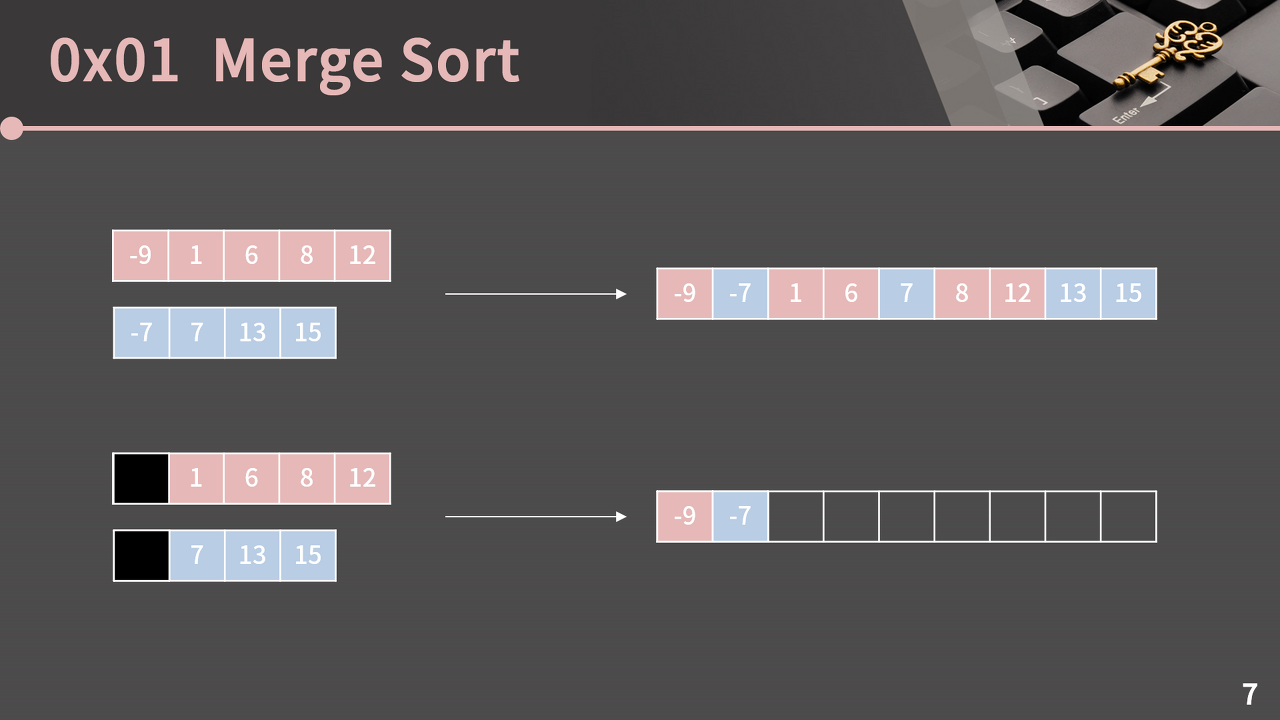
이 과정을 반복하면, 대소 비교 1번당 한 개의 원소 위치를 확정할 수 있으므로 시간복잡도는 O(N + M)이 된다.
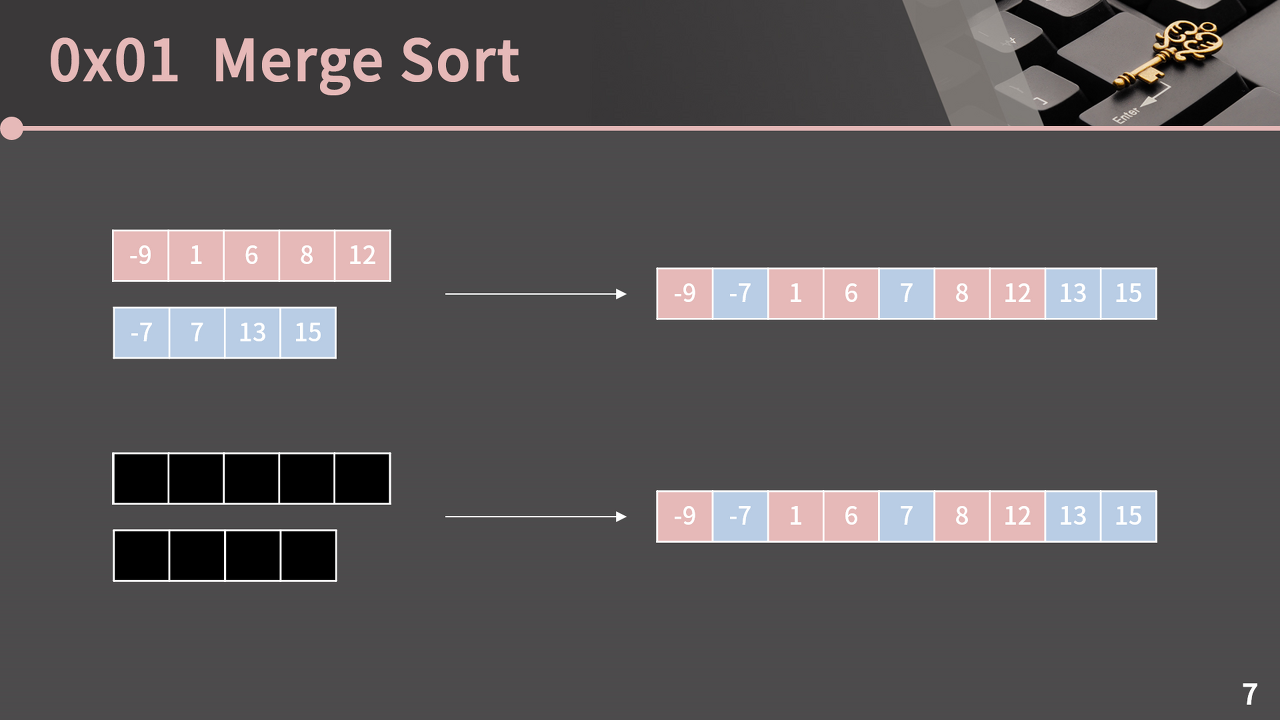
정렬된 두 배열 합치기
#include <bits/stdc++.h>
using namespace std;
int n, m;
int a[1000005], b[1000005], c[2000005];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for(int i = 0; i < n; i++) cin >> a[i];
for(int i = 0; i < m; i++) cin >> b[i];
}
void merge() {
int aidx = 0, bidx = 0;
for(int i = 0; i < n + m; i++) {
if(bidx == m) c[i] = a[aidx++];
else if(aidx == n) c[i] = b[bidx++];
else if(a[aidx] <= b[bidx]) c[i] = a[aidx++];
else c[i] = b[bidx++];
}
for(int i = 0; i < n + m; i++) cout << c[i] << " ";
}재귀를 이용한 분할 정복
머지 소트의 알고리즘은 아래 3단계로 요약할 수 있다.
- 주어진 배열을 2개로 나눈다.
- 각 배열을 정렬한다.
- 정렬된 두 배열을 합친다.
여기서 드는 의문은 '2번을 어떻게 구현하느냐'이다.
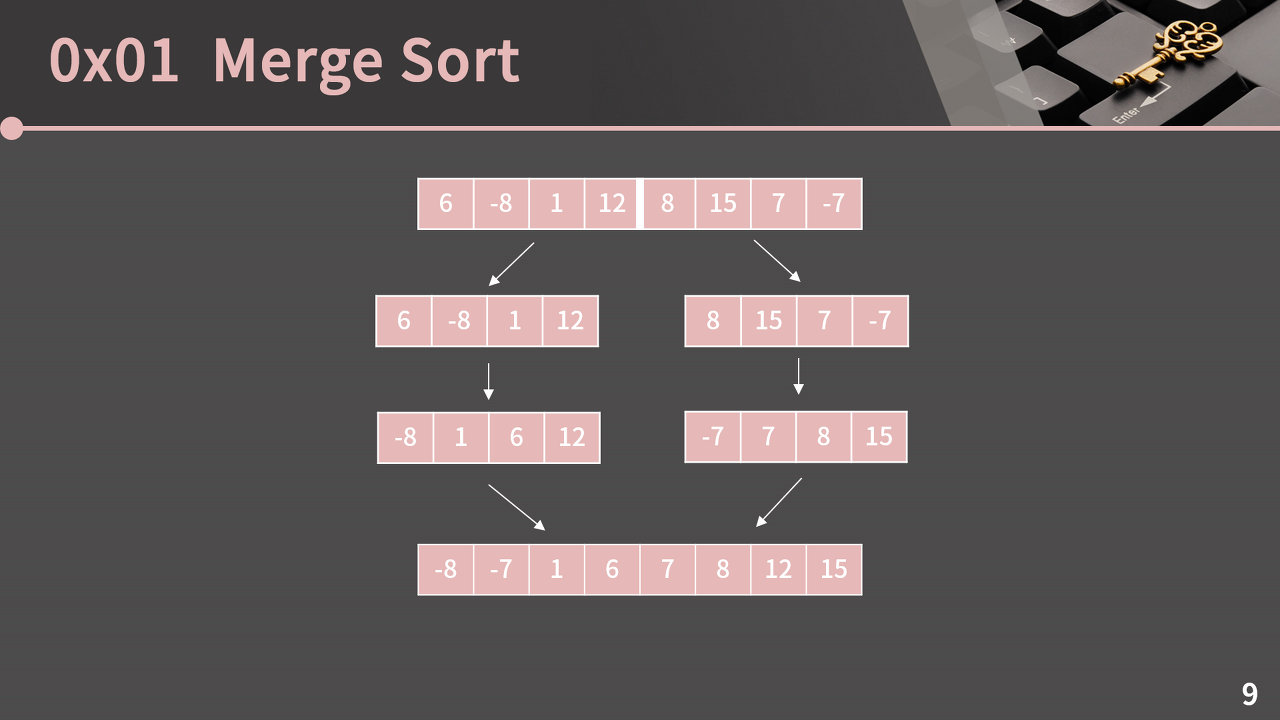
위의 그림에서 {6, -8, 1, 12} -> {-8, 1, 6, 12} 이를 어떻게 구현할까?
이것은 바로 '재귀'에서 힌트를 얻을 수 있다.
길이가 1인 배열을 정렬할 수 있다.
길이가 N인 두 정렬된 배열을 합칠 수 있다.
"길이가 N인 배열을 정렬할 수 있으면, 길이가 2N인 배열도 정렬할 수 있다."
길이가 8인 배열을 정렬하려면 길이가 4인 배열을 정렬할 수 있어야 하고, 길이가 4인 배열을 정렬하려면 길이가 2인 배열을 정렬할 수 있어야 하고, 길이가 2인 배열을 정렬하려면 길이가 1인 배열을 정렬할 수 있어야 한다. 그런데, 길이가 1인 배열은 이미 그 자체로 정렬된 것이므로, 결국 우리는 길이가 8인 배열을 정렬할 수 있다.

시간복잡도
실제 구현을 다루기 전에 머지 소트의 시간복잡도를 먼저 분석해보자.
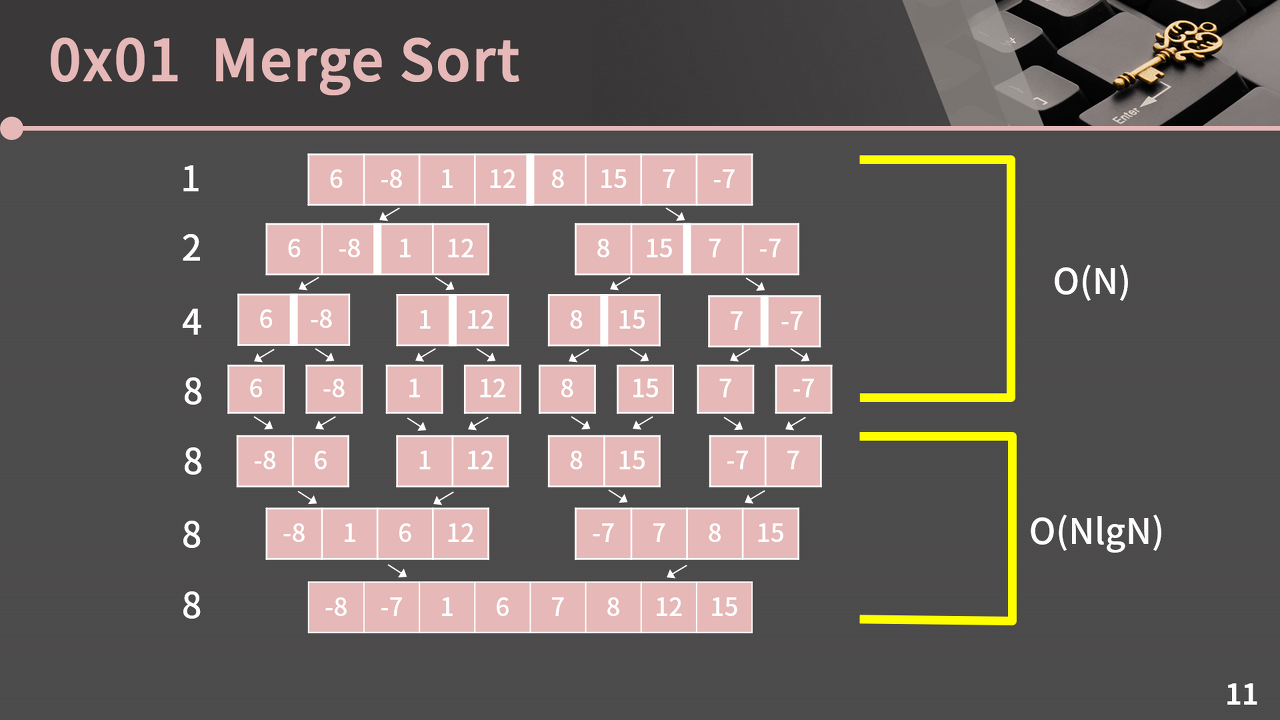
이렇게 전체 과정을 살펴보면 배열을 분할하는(Divide) 과정과 합치는(Conquer) 과정으로 구분할 수 있다. 위의 그림에서는 원소가 8개일 때를 예로 들었지만, 길이가 N = 2^k 인 배열로 확장해서 생각할 수 있다.
먼저 분할하는 과정은 특별한 연산을 하는 건 아니고, 그냥 함수 호출을 통해 관념적으로 분할되었다고 생각하는 것이다. 함수의 호출 횟수는 1 + 2 + 4 + ... + 2^k = 2^(k+1) - 1 = 2N - 1 즉, 빅오 표기법으로 O(N)이 된다.
다음으로, 분할된 배열을 합쳐나갈 때는 각 줄에서 모두 N번의 연산이 필요하다. 왜냐하면 앞서 "길이가 N, M인 정렬된 두 배열을 합치는 데는 O(N + M)의 시간복잡도가 걸린다"고 했다.
따라서, 각 라인에서 둘씩 짝지어 합쳐서 다음 단계로 넘어가려면, 결국 배열의 전체 길이만큼의 연산이 필요하다는 걸 알 수 있다.
1 + 1 + ... + 1
= 2 + 2 + 2 + 2
= 4 + 4
= 8
그리고 분할된 배열의 길이는 1에서 2^k가 될 때까지 2배씩 커지기 때문에, 합치는 단계는 총 k번 거치게 된다. 따라서 정렬된 배열을 다시 합치는 과정의 시간복잡도는 O(Nk) = O(NlogN)이 된다.
분할하는 과정은 O(N)이고 합쳐나가는 과정은 O(NlogN)인데, O(N)보다 O(NlogN)이 더 크기 때문에 최종적으로 머지 소트는 O(NlogN)의 시간복잡도를 가진다.
C++ 코드
참고: https://www.acmicpc.net/problem/2751
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1000001;
int n;
int arr[MAX];
int tmp[MAX]; // 추가적인 메모리 공간 필요
void conquer(int start, int end) {
int mid = (start + end) / 2;
int aidx = start;
int bidx = mid;
for(int i = start; i < end; i++){
if(bidx == end) tmp[i] = arr[aidx++];
else if(aidx == mid) tmp[i] = arr[bidx++];
else if(arr[aidx] <= arr[bidx]) tmp[i] = arr[aidx++];
else tmp[i] = arr[bidx++];
}
for(int i = start; i < end; i++) arr[i] = tmp[i];
}
void divide(int start, int end) {
// 더 이상 쪼갤 수 없을 때까지 재귀 호출
if(end - start == 1) return;
// 배열을 두 개로 나눈다.
int mid = (start + end) / 2;
divide(start, mid);
divide(mid, end);
// 정렬된 두 배열을 합친다.
conquer(start, end);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for(int i = 0; i < n; i++){
cin >> arr[i];
}
divide(0, n);
for(int i = 0; i < n; i++){
cout << arr[i] << "\n";
}
}Stable Sort
정렬된 두 배열을 합치는 코드에서, 두 원소의 크기가 동일할 때는 어떤 원소를 먼저 새 배열에 저장해야 할까?
#include <bits/stdc++.h>
using namespace std;
int n, m;
int a[1000005], b[1000005], c[2000005];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
for(int i = 0; i < n; i++) cin >> a[i];
for(int i = 0; i < m; i++) cin >> b[i];
}
void merge() {
int aidx = 0, bidx = 0;
for(int i = 0; i < n + m; i++) {
if(bidx == m) c[i] = a[aidx++];
else if(aidx == n) c[i] = b[bidx++];
else if(a[aidx] <= b[bidx]) c[i] = a[aidx++]; // 여기!
else c[i] = b[bidx++];
}
for(int i = 0; i < n + m; i++) cout << c[i] << " ";
}else if(a[aidx] <= b[bidx]) c[i] = a[aidx++];
위의 부등식에서 등호를 제외하면, Stable Sort라는 머지 소트의 성질을 만족시킬 수 없게 된다.
그렇다면, Stable Sort란 무엇일까?

위의 사람들을 나이 순으로 오름차순 정렬한다고 해보자. 나이가 21살로 동일한 사람들이 있기 때문에, 위의 그림과 같이 3가지 경우 모두 올바른 정렬이다. 이렇게 우선 순위가 같은 원소가 여러 개일 때는 정렬 결과가 유일하지 않을 수 있다. 그런데 그 중에서 우선 순위가 같은 원소들끼리는 원래의 순서를 따라가도록 하는 정렬이 Stable Sort이다.
즉, 정렬 전에 나이가 21살로 같은 사람들의 순서가 파랑, 빨강, 초록 순서라면, 정렬하고 나서도 이 순서는 동일하게 유지하는 것이다. 위의 그림에서 첫번째 정렬 결과가 Stable Sort이고, 그 아래 두 가지 결과는 Unstable Sort이다.
머지 소트는 Stable Sort이므로, 이 성질을 만족시키려면 쪼개진 두 배열에서 값이 동일한 원소가 있을 때는 원본 배열의 순서를 그대로 따르도록 구현해야 한다. 그래서 아까 언급했던 부등식에서 등호를 붙여줘야 하는 것이다.
퀵 정렬 (Quick Sort)
이름에서도 유추할 수 있듯이, 일반적으로 퀵 소트는 거의 모든 정렬 알고리즘보다 빨라서 각종 라이브러리의 정렬은 대부분 퀵 소트를 바탕으로 만들어져 있다.
🚫 그런데, 퀵 소트를 사용하며 매우x100 주의해야 할 점이 있다! 코딩테스트에서 STL을 못 쓰고 정렬을 직접 구현해야 한다면, 절대x100 퀵 소트를 쓰지 말고 머지 소트를 사용해야 한다는 것이다. 뒤에서 또 설명하겠지만, 퀵 소트는 최악의 경우 O(N^2)의 시간복잡도를 가지기 때문이다.
다시 본론으로 돌아와서, 퀵 소트는 머지 소트처럼 재귀적으로 구현되는 정렬이다. 퀵 소트는 매 단계마다 pivot(피벗)이라고 불리는 원소를 제자리로 보내는 작업을 반복한다. pivot은 배열 원소 중에 아무거나 잡으면 되는데, 편의상 제일 앞의 원소 6으로 잡겠다. (혹시 6이 아닌 다른 원소를 피벗으로 잡고 싶다면, 그냥 6과 자리만 바꿔주면 된다.)
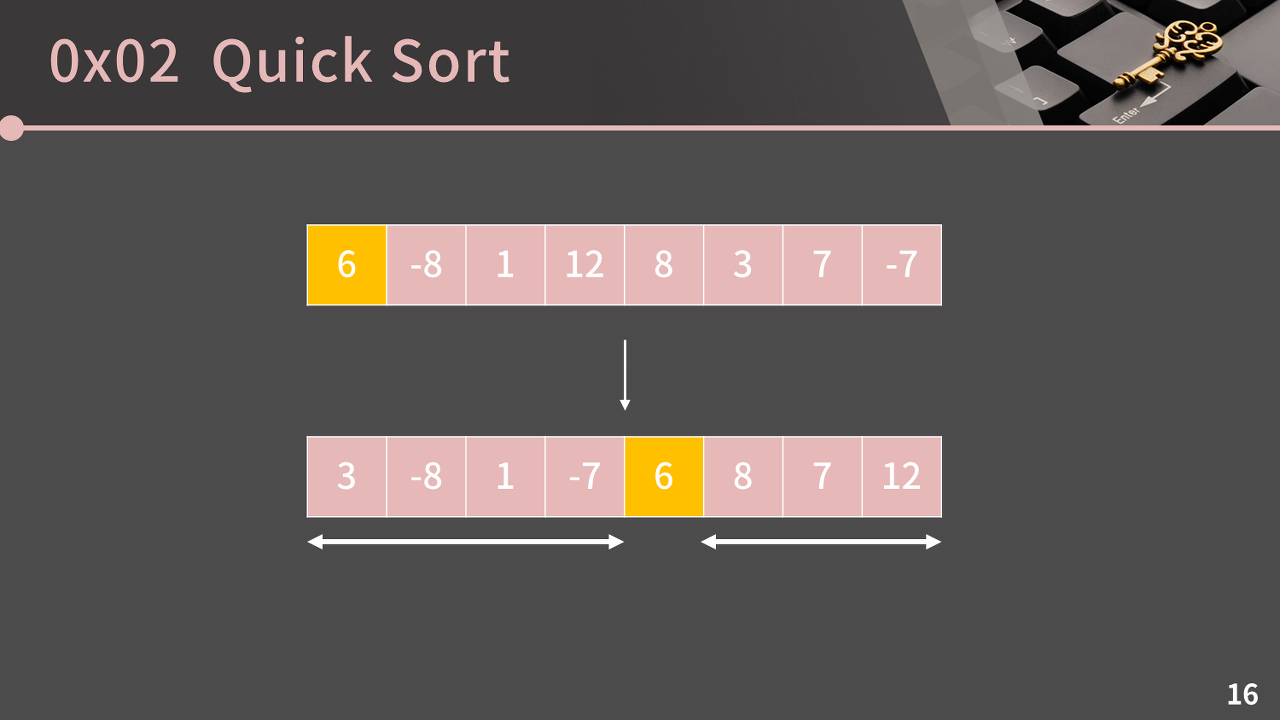
이제 피벗을 제자리로 보낼 건데, 제자리로 보낸다는 것의 의미는 "피벗보다 작은 값은 피벗의 왼쪽에, 피벗보다 큰 값은 피벗의 오른쪽에 두겠다"는 뜻이다.
피벗을 제자리로 보내고 나면, 피벗의 좌우로 나눠진 각 배열을 머지 소트에서 했던 재귀적인 방법으로 정렬해주면 된다.

피벗보다 작은 값은 피벗의 왼쪽에, 피벗보다 큰 값은 피벗의 오른쪽에 두는 방법은?
바로 떠오르는 방법은 위와 같다. 임시 배열 tmp를 만들고, 피벗을 제외한 나머지 원소들을 순회하며 피벗 이하의 값을 다 tmp에 넣는다. 그 다음에는 피벗을 담고, 다시 한번 배열을 순회하면서 피벗보다 큰 값을 다 tmp에 넣는다. 마지막으로 tmp 배열을 원본 배열에 덮어씌우면 된다.
이 방법은 배열 전체를 2번 순회하므로 O(N)에 동작하는 코드이다. 그런데, 이렇게 구현하면 퀵 소트의 장점을 뭉개버리는 것이나 다름없다!
퀵 소트는 추가적인 메모리 공간이 필요하지 않다는 게 큰 장점이다. 그리고 배열 안에서의 자리 바꿈만으로 정렬이 되기 때문에, cache hit rate이 높아서 속도가 빠르다는 장점도 있다.
따라서, 추가적인 메모리 공간을 사용하지 않고 피벗을 제자리로 보내는 방법을 고안해야 하며, 이렇게 추가적인 메모리 공간을 사용하지 않는 정렬을 In-Place Sort 라고 부른다.

위의 그림과 같이 피벗을 제외한 배열의 양끝에 포인터 두개를 두고 적절하게 스왑해주면, 추가적인 메모리 공간 없이도 피벗을 제자리에 보낼 수 있다.
left 포인터는 피벗보다 큰 값이 나올 때까지 오른쪽으로 이동, right 포인터는 피벗보다 작은 값이 나올 때까지 왼쪽으로 이동한다. 이동이 멈추면 두 포인터가 가리키는 원소의 값을 스왑한다. 이 과정을 left, right 포인터가 서로 교차할 때까지 반복하면 된다.
left, right 포인터가 교차하면, 피벗과 right을 마지막으로 스왑하여 정렬을 완료하면 된다.
C++ 코드
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1000001;
int n;
int arr[MAX];
void quickSort(int start, int end) {
// 더 이상 쪼갤 수 없으면 재귀 호출 종료
if (end - start <= 1) return;
// 피벗과 투포인터 세팅
int pivot = arr[start];
int l = start + 1;
int r = end - 1;
// 피벗을 제자리로 보낸다.
while(true) {
while(l <= r && arr[l] <= pivot) l++;
while(l <= r && arr[r] >= pivot) r--;
if(l > r) break;
swap(arr[l], arr[r]);
}
swap(arr[start], arr[r]);
// 피벗을 기준으로 나뉜 두 배열을 재귀적으로 정렬한다.
quickSort(start, r);
quickSort(r + 1, end);
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for(int i = 0; i < n; i++){
cin >> arr[i];
}
quickSort(0, n);
for(int i = 0; i < n; i++){
cout << arr[i] << "\n";
}
}시간복잡도
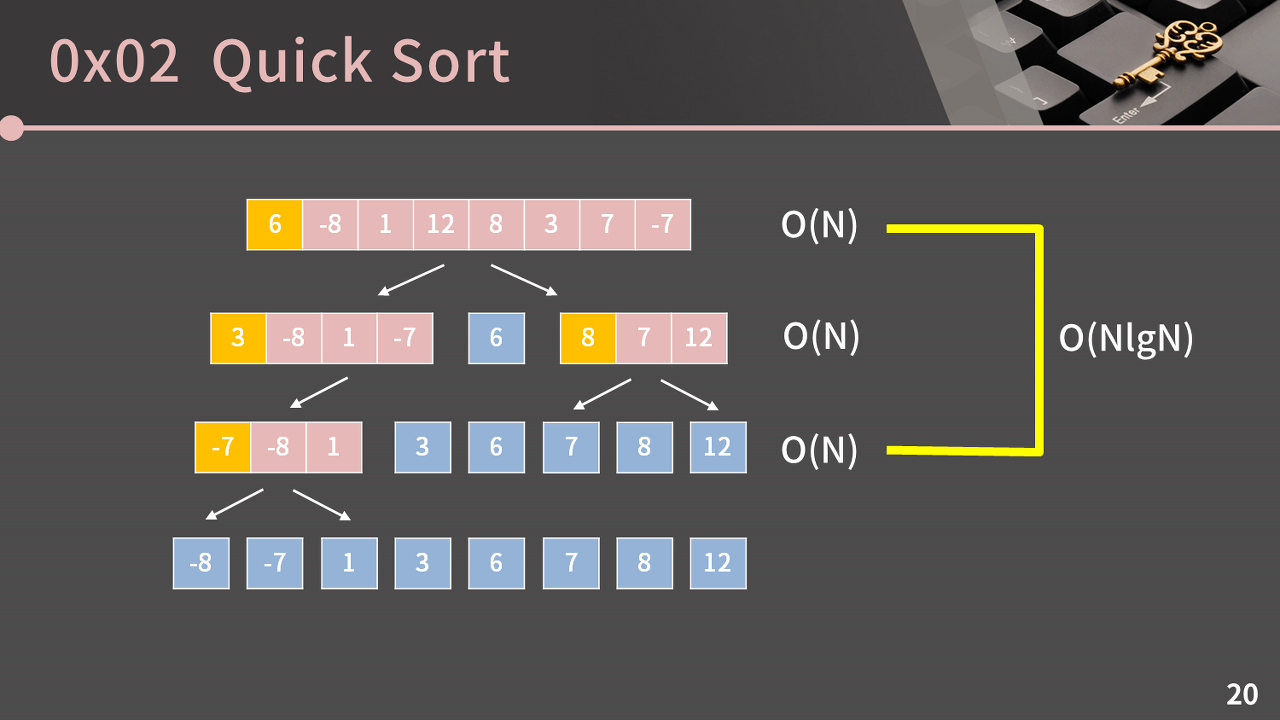
투포인터를 이용하여 피벗을 제자리로 보내는 시간복잡도는, 주어진 배열 크기에 비례하므로 각 단계마다 O(N)이라고 볼 수 있다. 그리고 피벗이 매번 완벽하게 중앙에 위치하여 배열을 균등하게 쪼갠다면, 각 단계의 수는 머지 소트 때와 마찬가지로 logN일 것이다.
따라서, 퀵 정렬의 평균 시간복잡도는 O(NlogN)이다. 그리고 cache hit rate 또한 높아서 퀵 정렬은 속도가 굉장히 빠르다.
그런데, 퀵 정렬은 아주 치명적인! 단점이 있다.
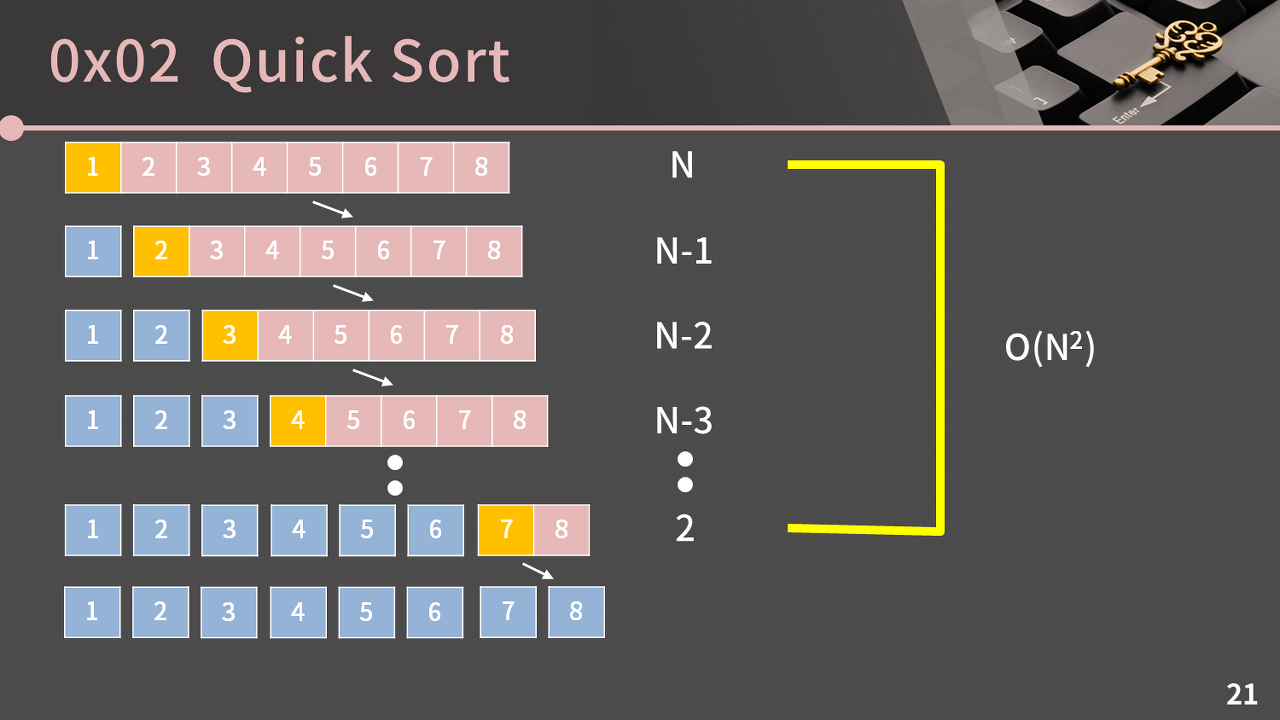
위와 같이 이미 정렬된 배열을 퀵 소트로 정렬하면 어떻게 될까? 안타깝게도 매 단계마다 피벗은 중앙이 아니라 제일 왼쪽에 위치하게 된다. 이로 인해 단계 수는 logN이 아니라, N이 된다. 따라서, 최악의 경우 퀵 정렬은 O(N^2)의 시간복잡도를 갖게 된다.
그럼 대부분의 라이브러리에서는 퀵 정렬의 이러한 단점을 어떻게 처리한 것일까?
실제로는 피벗을 랜덤하게 선택할 수도 있고, 피벗 후보를 3개 정해서 그 중에서 중앙값으로 피벗을 설정하기도 한다. 그리고 최악의 경우에도 O(NlogN)을 보장하기 위해, 일정 깊이 이상 들어가면 퀵 소트 대신에 O(NlogN)이 보장되는 힙 소트로 정렬한다. 참고로 이러한 정렬을 introspective sort라 부른다.
머지 소트 vs 퀵 소트
| 머지 소트 | 퀵 소트 | |
|---|---|---|
| 시간복잡도 | O(NlogN) | 평균 O(NlogN), 최악 O(N^2) (단, 평균적으로 머지 소트보다 빠름) |
| 추가적으로 필요한 공간 (오버헤드) | O(N) | O(1) |
| In-Place Sort | X | O |
| Stable Sort | O | X |
카운팅 정렬 (Counting Sort)
앞서 살펴본 머지 소트, 퀵 소트 모두 배열 원소의 값을 비교하여 정렬하는 Comparison Sort이다.
반면에, 원소의 값을 비교하지 않고 정렬할 수 있는 방법도 있다! 카운팅 정렬이 그 방법 중에 하나이다.
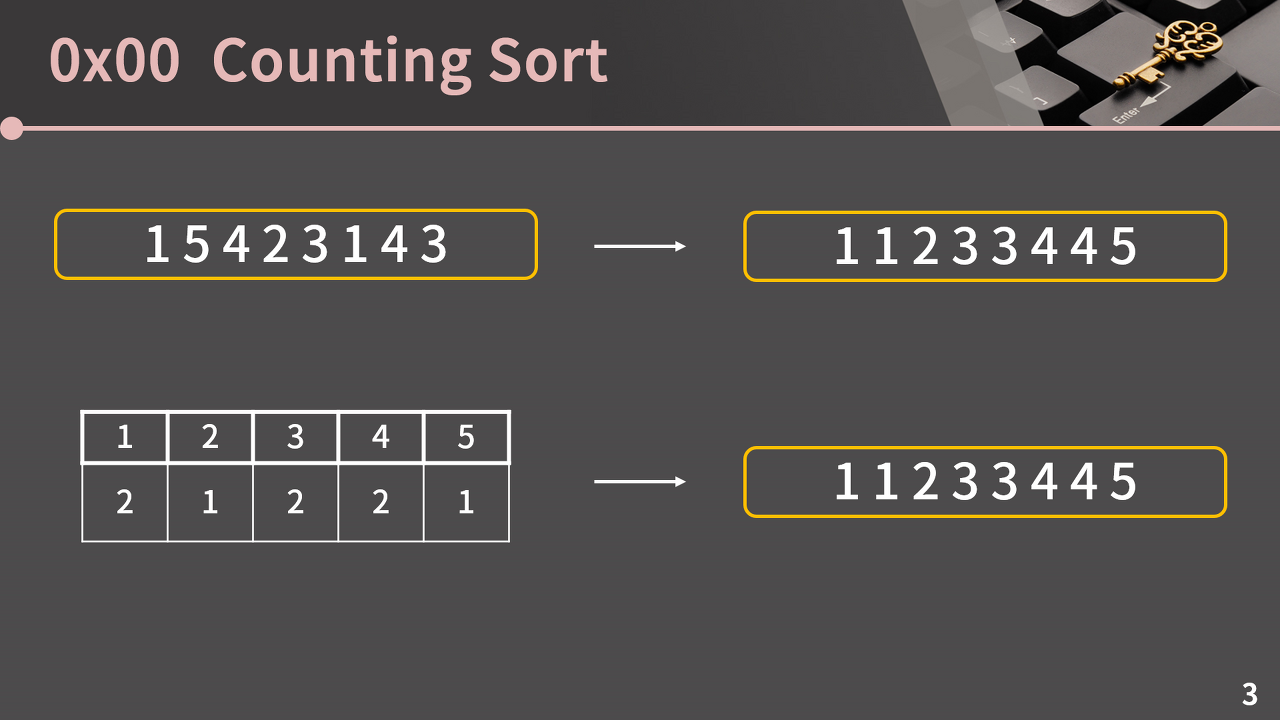
위의 표에 보이는 것처럼 배열 원소들의 등장 횟수를 별도로 기록해두고, 그 횟수만큼 원소를 출력하면 그대로 정렬된 결과를 얻을 수 있다.
너무나도 쉬운 방법이지만, 만능이 아니라는 것에 주의해야 한다!
일단 배열 원소의 등장 횟수를 구하려면, 미리 크기가 큰 테이블을 만들어두고 숫자에 대응되는 원소의 값을 1 증가시켜서 처리하면 된다.
배열 원소의 범위가 0~9 라고 하면 freq[10], 0~9999 라고 하면 freq[10000] 배열을 만들면 된다. 그런데 만약 수의 범위가 0~999,999,999 라고 하면 크기가 10억인 배열이 필요하다. 메모리 제한이 512MB라고 해도 int 기준으로 대략 1.2억 크기의 배열밖에 잡을 수 없으니 카운팅 소트를 사용할 수 없다.
따라서, 카운팅 소트는 수의 범위가 대략 1000만 이하일 때만 사용하고, 그보다 범위가 커지면 사용하기 어렵다고 생각하면 된다.
15688번. 수 정렬하기 5
https://www.acmicpc.net/problem/15688
#include <iostream>
using namespace std;
const int MAX = 2000001;
int freq[MAX];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int n;
cin >> n;
for(int i = 0; i < n; i++){
int a;
cin >> a;
freq[a + 1000000]++;
}
for(int i = 0; i < MAX; i++){
while(freq[i]--){
cout << i - 1000000 << "\n";
}
}
}시간복잡도
수의 범위가 K개라고 할 때, 맨 처음 N개의 수를 보면서 freq 배열을 초기화 해주고, 답을 출력할 때 (또는 정렬을 수행할 때) 총 K칸의 값을 확인해야 하므로, 시간복잡도는 O(N + K)이다.
즉, 수의 범위 K가 작을 때는 카운팅 소트가 굉장히 효율적인 방법이지만, 수의 범위가 크면 카운팅 소트를 사용할 수 없다는 것을 기억하자.
11652번. 카드
https://www.acmicpc.net/problem/11652
입력 범위가 -2^62 ~ 2^62 라는 것에 매우 유의해야 하는 문제이다!
카운팅 정렬은 입력되는 숫자의 범위가 1000만 이하일 때 적합하므로, 이 문제에서는 사용할 수 없다.
정렬된 배열은 "중복된 원소끼리 서로 인접하다"는 성질을 이용하여 다음과 같이 정답을 구할 수 있다.
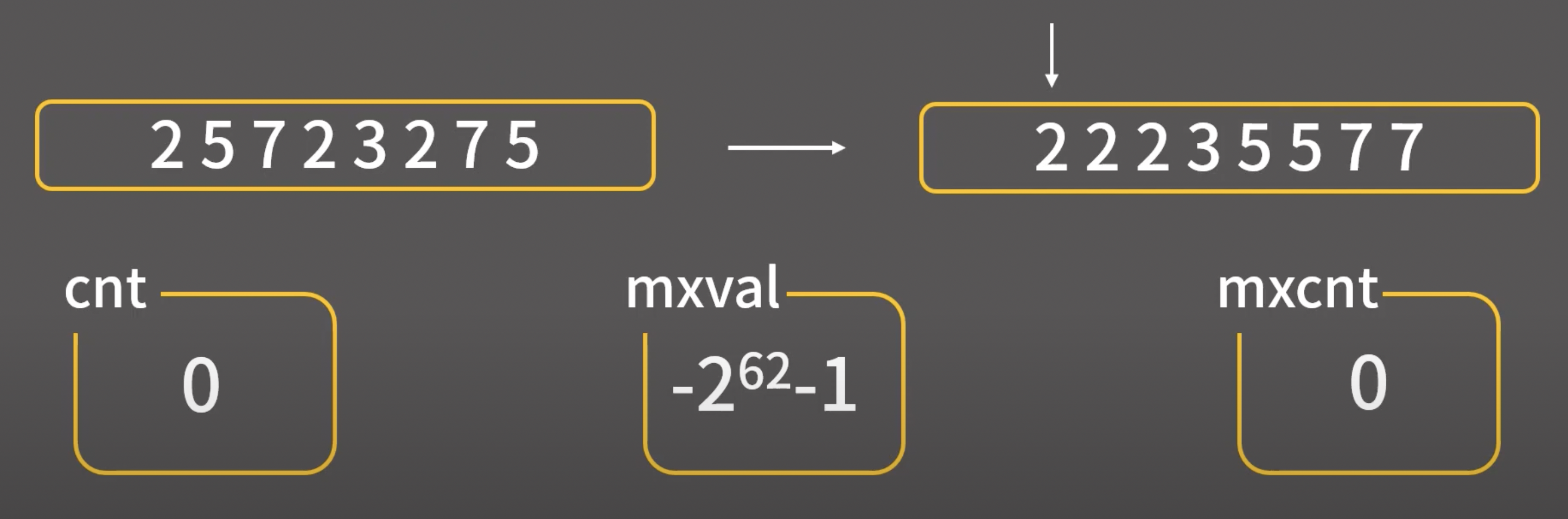
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cmath>
#include <map>
using namespace std;
typedef pair<int, int> pii;
typedef long long ll;
int N;
vector<ll> arr;
void input() {
cin >> N;
for(int i = 0; i < N; i++){
ll num;
cin >> num;
arr.push_back(num);
}
}
void solution() {
sort(arr.begin(), arr.end());
int cnt = 0; // 현재 숫자의 등장 횟수
int maxCnt = 0; // 같은 숫자의 최대 등장 횟수
ll answer = -(1LL << 62) -1;
// 현재 숫자의 등장 횟수를 구하고
// 다른 숫자가 등장하면, 최대 등장 횟수 갱신하기
for(int i = 0; i < N; i++){
// 현재 숫자의 등장 횟수 구하기
// 이전과 같은 숫자인지 검사 (정렬된 배열이므로)
if(i == 0 || arr[i - 1] == arr[i]) cnt++;
else{
// 다른 숫자가 등장하면
// 현재까지의 최대 등장 횟수와 그 원소값 갱신하기
if(maxCnt < cnt) {
maxCnt = cnt;
answer = arr[i - 1];
}
// 현재 숫자에 대한 등장 횟수 초기화
cnt = 1;
}
}
// 마지막 원소에 대한 처리
if(maxCnt < cnt) {
answer = arr[N - 1];
}
cout << answer;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
input();
solution();
return 0;
}은근히 조건 처리하기 까다로운 문제이다!

