참고 영상: https://youtu.be/CyINCmJPjfM

소수 (Prime number)란 1보다 큰 자연수 중에서 1과 자기 자신만을 약수로 갖는 자연수이다. 여기서 약수란 어떤 수를 나누어 떨어지게 하는 0이 아닌 정수이므로, 결국 소수는 1보다 큰 자연수 중에서 1과 자기 자신만으로 나누어 떨어지는 자연수이다. 1과 자기 자신을 제외한 자연수로도 나누어 떨어진다면 그 수는 소수가 아니라고 판별할 수 있다.

• 6은 1, 2, 3, 6으로 나누어 떨어지므로 소수가 아니다.
• 7은 1과 7을 제외하고는 나누어 떨어지지 않으므로 소수이다.

기본 알고리즘

#include<iostream>
using namespace std;

bool isPrimeNumber(int x) {
    if (x < 2) // 소수의 정의에서 벗어난 수들은 예외 처리
        return false;
        
    // 2부터 (x-1)까지의 모든 수를 확인하며
    for (int i = 2; i < x; i++) {
        // x가 해당 수로 나누어 떨어진다면
        if (x % i == 0) {
            return false; // i는 x의 약수이고, x는 소수가 아님.
        }
    }
    
    return true;
}

int main(){
    cout << isPrimeNumber(3) << '\n'; // 1 
    cout << isPrimeNumber(4) << '\n'; // 0 

    return 0;
}

위 코드는 2부터 (x-1)까지의 모든 자연수를 하나씩 확인하므로 시간 복잡도가 O(n)이다. 다시 말해 소수인지 확인하려는 수의 값이 커지면 커질수록 이에 선형적으로 비례하는 시간이 소요된다는 뜻이다. 예를 들어 10억이 소수인지 판별하려면 2부터 (10억 - 1)까지의 모든 수에 대해서 연산을 수행해야 한다.

약수의 성질

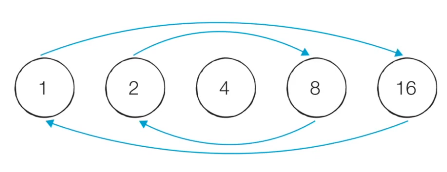
위의 방법보다 효율적인 알고리즘을 구현하기 위해 약수가 갖는 성질을 생각해볼 수 있다. 모든 약수는 가운데 약수를 기준으로 곱셈 연산에 대해 대칭을 이루는 성질이 있다. 예를 들어 16의 약수는 1, 2, 4, 8, 16인데, 이때 2 * 8 = 8 * 2 = 16 이므로 약수들이 서로 곱셈에 대해 대칭이라는 걸 알 수 있다.
따라서 특정한 자연수의 모든 약수를 찾고 싶을 때, 가운데 약수 (제곱근)까지만 확인하면 된다. 예를 들어 16이 2로 나누어 떨어진다는 것은 8로도 나누어 떨어진다는 뜻이므로, 16의 모든 약수를 보다 빠른 속도로 구할 수 있다.

개선된 알고리즘

약수의 성질을 이용하여 소수 판별 알고리즘을 개선해보자. 2부터 (x-1)까지가 아니라, x의 제곱근까지만 수를 확인해도 x의 약수들을 구할 수 있다. 그리고 이를 통해 x가 소수인지 아닌지 확인할 수 있다.

#include<iostream>
#include<cmath>
using namespace std;

bool isPrimeNumber(int x) {
    if (x < 2) // 소수의 정의에서 벗어난 수들은 예외 처리
        return false;
        
    // 2부터 x의 제곱근까지 모든 수를 확인하며
    for (int i = 2; i <= (int)sqrt(x); i++) {
        // x가 해당 수로 나누어 떨어진다면 
        if (x % i == 0) {
            // i와 그에 대칭인 수는 모두 x의 약수이고, x는 소수가 아님.
            return false; 
        }
    }
    
    return true;
}

int main(){
    cout << isPrimeNumber(15) << '\n'; // 0

    return 0;
}

2부터 x의 제곱근 (소수점 무시) 까지의 모든 자연수에 대해 연산을 수행하므로 이 알고리즘의 시간 복잡도는 O($\sqrt{n}$)이다.

다수의 소수 판별

위의 알고리즘들을 이용하면 '하나의 수'가 소수인지 아닌지 판별할 수 있다. 하지만, 특정한 수의 범위 안에 존재하는 모든 소수를 찾고 싶을 때는 어떻게 해야 할까? 이때는 에라토스테네스의 체 알고리즘을 사용할 수 있다.

에라토스테네스의 체 알고리즘

• 다수의 자연수에 대하여 소수 여부를 판별할 때 사용하는 대표적인 알고리즘이다.
• 에라토스테네스의 체는 N 이하의 모든 소수를 찾을 때 사용할 수 있다.
• 구체적인 동작 과정은 다음과 같다.

1. 2부터 N까지의 모든 자연수를 나열한다.
2. 남은 수 중에서 아직 처리하지 않은 가장 작은 수 i를 찾는다.
3. 남은 수 중에서 (i 자신을 제외한) i의 배수를 모두 제거한다.
4. 더 이상 반복할 수 없을 때까지 2, 3번 과정을 반복한다.
5. 마지막까지 제거되지 않고 남은 수들이 모두 소수이다.

#include<iostream>
#include<cmath>
#include<vector>
using namespace std;

int main(){
	int n = 1000; // 2부터 1000까지의 모든 수에 대해서 소수 판별 
	vector<bool> prime(n + 1, true); // 처음엔 모든 수가 소수인 것으로 초기화 (0과 1은 제외)
	prime[0] = false; 
	prime[1] = false;
	
    // 2부터 n의 제곱근까지 모든 수를 확인하며
    for (int i = 2; i <= (int)sqrt(n); i++) {
        if (prime[i]) { // 지워지지 않은 숫자들에 대해서 
			// i 자신을 제외한 i의 배수 모두 지우기 
			for(int j = 2 * i; j <= n; j += i){ 
				prime[j] = false; 
			}
        }
    }

    for (int i = 2; i <= n; i++) {
        if (prime[i]) cout << i << " ";
    }

    return 0;
}

이 알고리즘의 시간 복잡도는 O(Nlog(logN))으로 사실상 선형 시간에 가까울 정도로 매우 빠르며, 다수의 소수를 찾아야 하는 문제에서 효과적으로 사용될 수 있다.
하지만, 각 자연수에 대한 소수 여부를 저장해야 하므로 메모리가 많이 필요하다. 예를 들어 10억 이하의 모든 자연수에 대해서 소수 여부를 판별하려면, 메모리 측면에서 매우 비효율적일 수도 있다. 이런 점을 유념하여 사용하도록 하자.

관련 백준 문제

2501번: 약수 구하기

https://www.acmicpc.net/problem/2501

• 두 개의 자연수 N과 K가 주어졌을 때, N의 약수들 중 K번째로 작은 수를 출력하라.
• N은 1 이상 10,000 이하, K는 1 이상 N 이하
• 만일 N의 약수의 개수가 K개보다 적어서 K번째 약수가 존재하지 않을 경우에는 0을 출력

#include<iostream>
using namespace std;

int main() {
	int n, k;
	cin >> n >> k;

	int cnt = 0; // k번째 약수를 찾기 위한 변수 
	for (int i = 1; i <= n; i++) {
		if (n % i == 0) {
			cnt++;
			if (cnt == k) {
				cout << i << "\n";
			}
		}
	}

	if (cnt < k)
		cout << "0\n";

	return 0;
}

2581번: 소수

https://www.acmicpc.net/problem/2581

• M이상 N이하의 자연수 중 소수인 것을 모두 골라 이들 소수의 합과 최솟값을 찾아라.
• M과 N은 10,000이하의 자연수이며, M은 N보다 작거나 같다.
• 단, M이상 N이하의 자연수 중 소수가 없을 경우는 첫째 줄에 -1을 출력한다.

#include<iostream>
using namespace std;

bool isPrimeNumber(int x) {
    if (x < 2) 
        return false;

    // 2부터 x의 제곱근까지 모든 수를 확인하며 
    for (int i = 2; i * i <= x; i++) {
        // x가 해당 수로 나누어 떨어진다면 
        if (x % i == 0) {
            // i와 그에 대칭인 수는 모두 x의 약수이고, x는 소수가 아님.
            return false;
        }
    }

    return true;
}

int main() {
    int m, n;
    cin >> m >> n;

    int sum = 0, min = -1;
    for (int i = m; i <= n; i++) {
        if (isPrimeNumber(i)) {
            sum += i;
            if (min == -1) // not updated
                min = i;
        }
    }

    if (sum == 0)
        cout << "-1";
    else {
        cout << sum << "\n" << min;
    }

    return 0;
}

1929번. 소수 구하기

https://www.acmicpc.net/problem/1929

M이상 N이하의 소수를 모두 출력하는 프로그램을 작성하시오.

기본 알고리즘: O($\sqrt{n}$)

#include <iostream>
#include <vector>
#include <cmath>
using namespace std;

bool isPrimeNumber(int x){
	if(x < 2) return false; 

	for(int i = 2; i <= (int)sqrt(x); i++){
		if(x % i == 0) return false; 
	}

	return true; 
}

int main()
{	
	int m, n; 
	cin >> m >> n;

	for(int i = m; i <= n; i++){
		if(isPrimeNumber(i)) cout << i << "\n";
	}

    return 0;
}

에라토스테네스의 체: O(Nlog(logN))

#include <iostream>
#include <vector>
#include <cmath>
using namespace std; 

int main()
{	
	int m, n; 
	cin >> m >> n;

	vector<bool> prime(n + 1, true);
	prime[0] = false; 
	prime[1] = false; 

	for(int i = 2; i <= (int)sqrt(n); i++){
		if(prime[i]){ // 지워지지 않은 숫자들에 대해서 
			// i 자신을 제외한 i의 배수 모두 지우기 
			for(int j = 2 * i; j <= n; j += i){ 
				prime[j] = false;
			}
		}
	}

	for(int i = m; i <= n; i++){
		if(prime[i]) cout << i << "\n"; 
	}

    return 0;
}