참고 영상: https://youtu.be/xeSz3pROPS8
위상 정렬
사이클이 없는 방향 그래프 (DAG, directed acyclic graph)의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것을 의미한다. 즉, 순서가 정해져있는 작업을 차례로 수행해야 할 때, 그 순서를 결정하기 위해 사용하는 정렬 알고리즘이다.
ex1) 선수 과목을 고려한 수강 신청
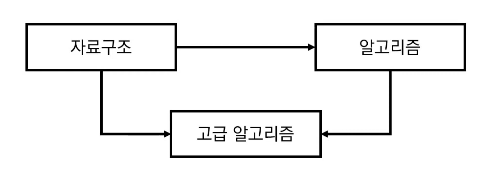
위 세 과목을 모두 듣기 위한 적절한 학습 순서는?
- 자료구조 → 알고리즘 → 고급 알고리즘 (O)
- 자료구조 → 고급 알고리즘 → 알고리즘 (X)
ex2) 졸업 요건 채우기
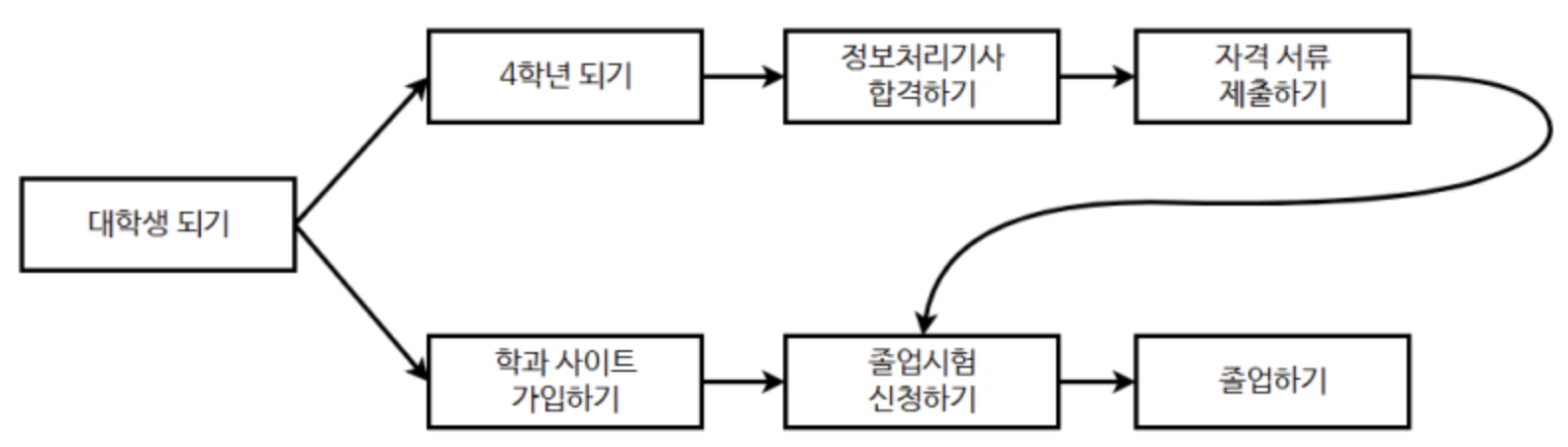
위의 그림에서 졸업요건을 충족시키기 위한 적절한 순서는?
대학생 되기 → 학과 사이트 가입하기 → 4학년 되기 → 정처기 합격 → 자격 서류 제출 → 졸업시험 신청 → 졸업
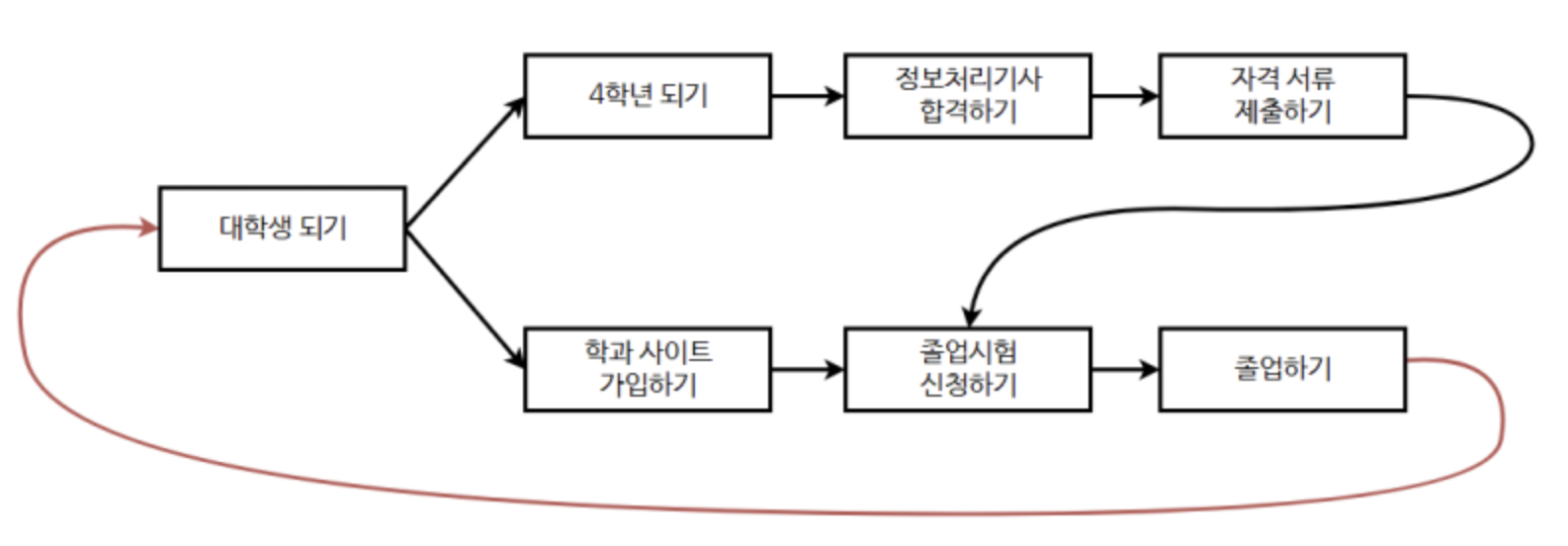
사이클이 발생하는 경우 모든 노드의 진입차수가 1 이상이므로, 첫번째 시작점을 정할 수 없어서 위상 정렬을 수행할 수 없다. 따라서, 진입차수가 0인 노드가 적어도 하나 존재해야 하므로, 위상 정렬은 사이클이 없는 방향 그래프에서만 수행할 수 있다.
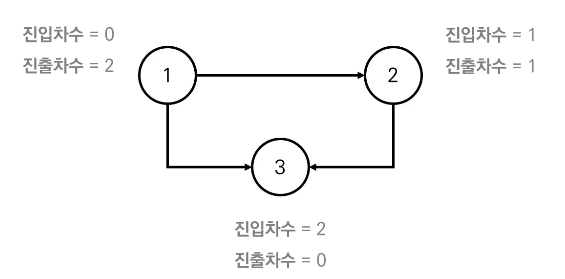
진입차수와 진출차수
- 진입차수 (Indegree): 특정한 노드로 들어오는 간선의 개수
- 진출차수 (Outdegree): 특정한 노드에서 나가는 간선의 개수
위상 정렬 알고리즘
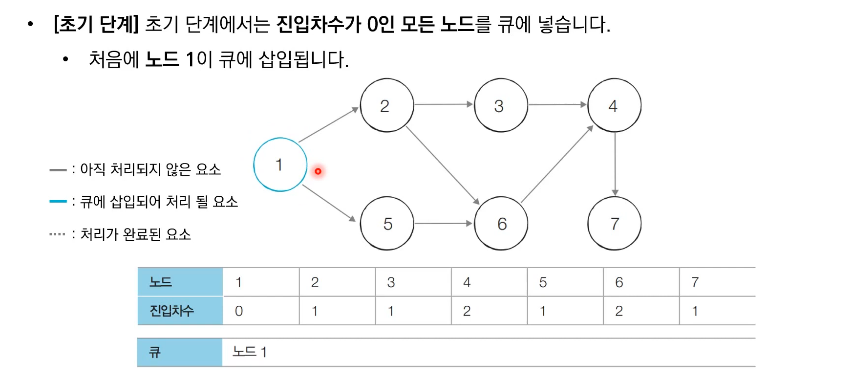
큐를 이용하는 위상 정렬 알고리즘의 동작 과정은 다음과 같다.
- 진입차수가 0인 모든 노드를 큐에 넣는다.
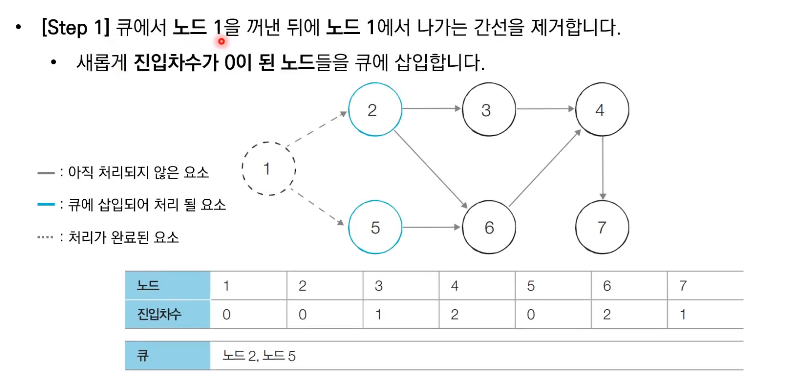
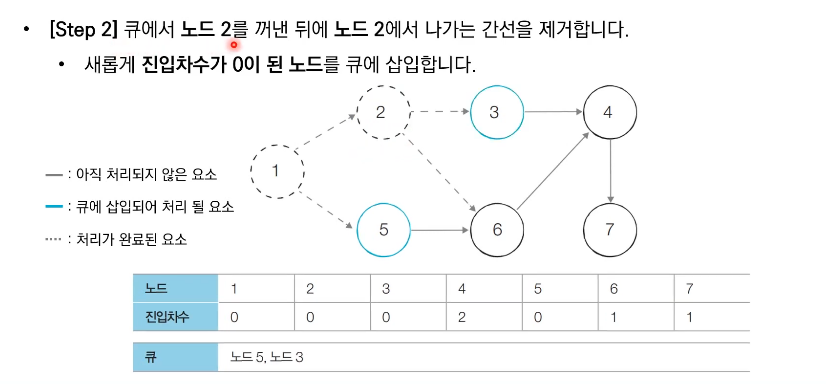
- 큐가 빌 때까지 다음의 과정을 반복한다.
1) 큐에서 원소를 꺼내 해당 노드에서 나가는 간선을 하나씩 제거한다.
2) 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
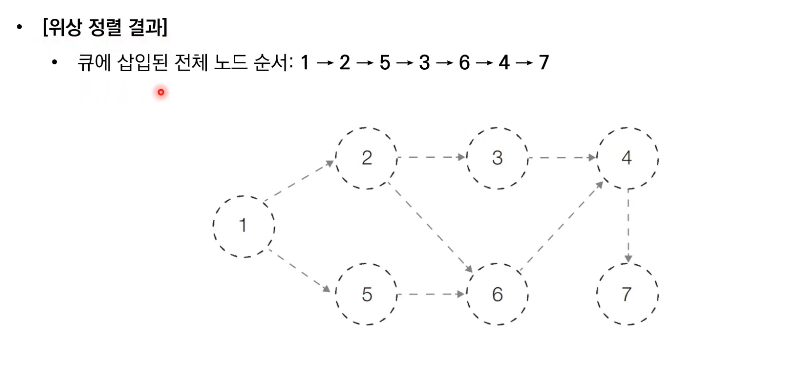
→ 결과적으로 각 노드가 큐에 들어온 순서가 위상 정렬을 수행한 결과와 같다!
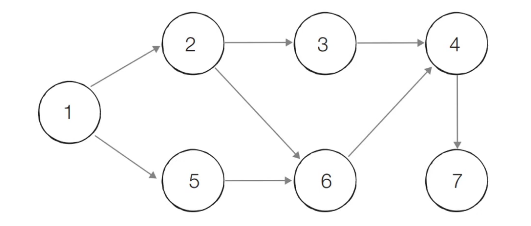
위상 정렬 동작 예시
위상 정렬을 수행할 그래프를 준비한다. 이때 그래프는 사이클이 없는 방향 그래프 (DAG)여야 한다. (만약 사이클이 존재한다면 해당 사이클의 모든 노드는 진입차수가 1 이상이므로, 위에서 설명한 알고리즘을 적용할 수 없게 된다.)
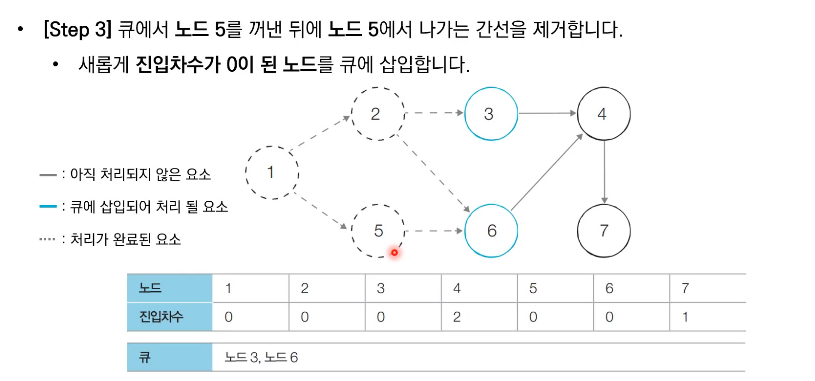
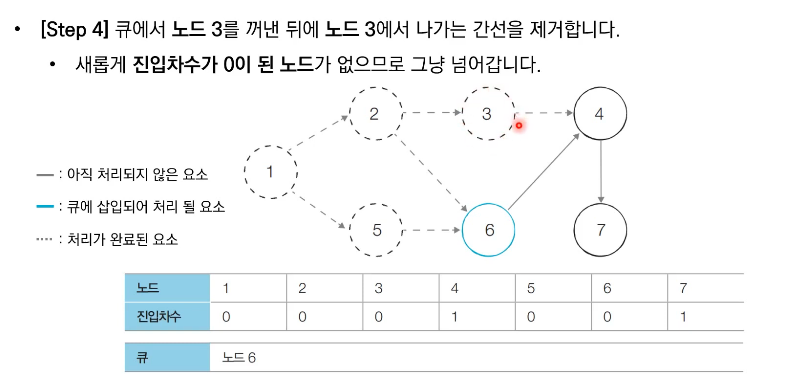
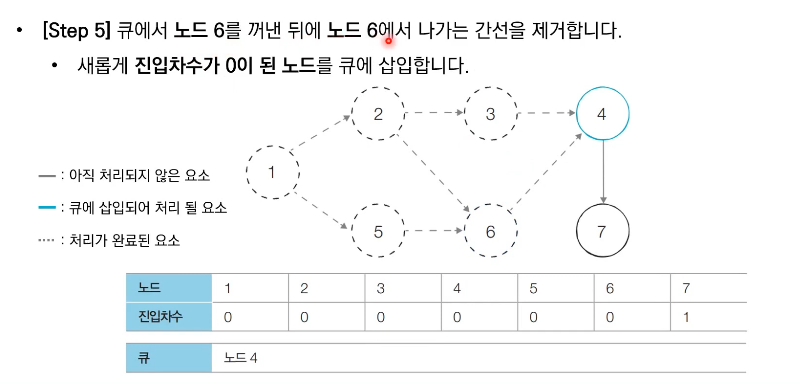
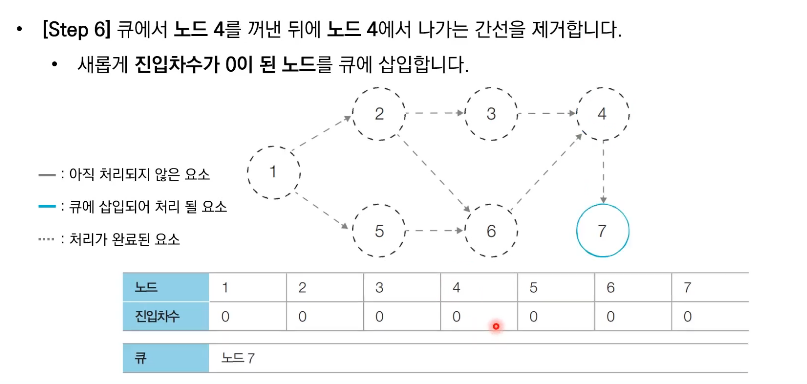
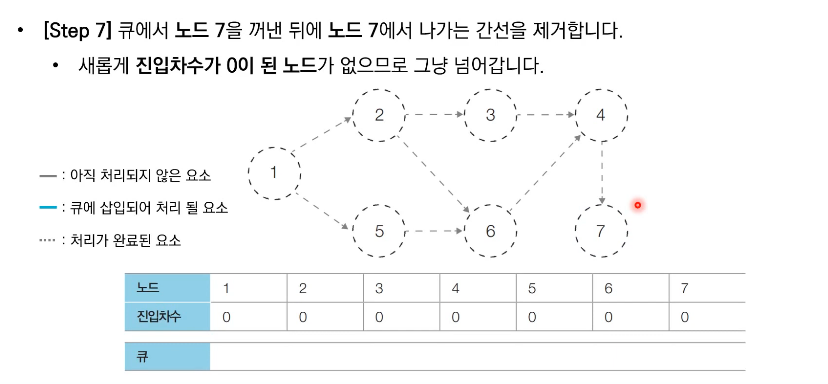
위상 정렬의 특징
- 위상 정렬은 DAG (순환하지 않는 방향 그래프)에 대해서만 수행할 수 있다.
- 위상 정렬에는 여러가지 답이 존재할 수 있다. 한 단계에서 큐에 새롭게 들어가는 원소가 2개 이상이면, 넣는 순서에 따라 여러가지 답이 나올 수 있다.
- 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다. 왜냐하면, 사이클에 포함된 모든 원소들은 진입차수가 1 이상이므로 큐에 들어가지 못하기 때문이다.
- 스택을 활용한 DFS를 이용해 위상 정렬을 수행할 수도 있다. (참고: https://sorjfkrh5078.tistory.com/36)
코드로 구현
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
int v, e; // 노드 개수, 간선 개수
int indegree[100001]; // 노드 개수 최대 10만개
vector<int> graph[100001]; // 각 노드에 연결된 노드 번호 저장
void topologySort(){
vector<int> result; // 정렬 결과를 저장
queue<int> q;
// 진입차수가 0인 노드를 큐에 삽입
for(int i = 1; i <= v; i++){
if(indegree[i] == 0){
q.push(i);
}
}
while(!q.empty()){
int now = q.front();
q.pop();
result.push_back(now);
// 해당 원소와 연결된 노드들의 진입차수에서 1 빼기 (간선 제거)
for(int i = 0; i < graph[now].size(); i++){
indegree[graph[now][i]] -= 1;
// 새롭게 진입차수가 0이 되는 노드들을 큐에 삽입
if(indegree[graph[now][i]] == 0){
q.push(graph[now][i]);
}
}
}
// 위상 정렬을 수행한 결과 출력
for(auto e: result)
cout << e << " ";
cout << "\n";
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> v >> e;
// DAG의 모든 간선 정보 입력 받기
for(int i = 0; i < e; i++){
int a, b;
cin >> a >> b;
graph[a].push_back(b); // 정점 a에서 b로 이동 가능
indegree[b] += 1; // b의 진입차수 증가
}
topologySort();
return 0;
} 입력
7 8
1 2
1 5
2 3
2 6
3 4
4 7
5 6
6 4
출력
1 2 5 3 6 4 7

