K-Means Clustering

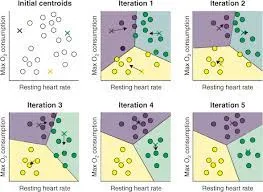
• 데이터를 몇 개의 클러스터로 나누는 비지도 학습 알고리즘
• 특징
  • 거리 기반 알고리즘으로, 데이터 간의 거리(유사성)를 계산하여 클러스터 형성
  • 데이터 스케일링(정규화) 필수
• 유사성이 높은 데이터는 같은 클러스터로, 유사성이 낮은 데이터는 다른 클러스터로 할당

알고리즘 순서

로이드 알고리즘 (Lloyd's Algorithm)

1. 초기 클러스터 중심(K개의 중심) 설정
   • 데이터에서 K개의 중심을 무작위로 선택한다.
2. 거리 계산
   • 각 데이터 포인트와 모든 클러스터 중심 간의 거리를 계산한다.
   • 주로 유클리드 거리 사용한다.
3. 클러스터 할당:
   • 각 데이터 포인트를 가장 가까운 클러스터 중심에 할당한다.
4. 중심 업데이트:
   • 각 클러스터의 데이터 평균을 계산하여 새로운 클러스터 중심으로 설정한다.
5. 반복
   • 클러스터 할당과 중심 업데이트를 반복하여 클러스터 중심이 더 이상 변화하지 않을 때까지 수행한다.

엘칸 알고리즘 (Elkan's Algorithm)

• K-means의 계산 효율성을 높인 최적화 버전으로, 불필요한 거리 계산을 줄이는데 초점을 둔다.
• 삼각 부등식을 활용하여, 데이터 포인트와 클러스터 중심 간 거리를 계산하지 않아도 되는 경우를 효율적으로 판별한다.

1. 각 클러스터 중심 간의 거리를 계산하여 저장한다.
2. 삼각 부등식을 사용해 데이터 포인트와 클러스터 중심 간 거리를 계산하지 않아도 되는 상황을 식별한다.
   • 예: 데이터가 이전 클러스터 중심에 더 가깝다고 보장되면 다른 중심과의 거리 계산을 생략
3. 나머지는 로이드 알고리즘과 동일하게 작동한다.

K개의 중심 초기화 방법

• 랜덤 초기화
  • 가장 기본적인 방법으로, 데이터를 무작위로 선택해 중심으로 설정
  • 간단하지만, 부적절한 초기화로 지역 최적값에 빠질 가능성이 있다.
• K-means++
  • 효율적인 초기화 방법으로, 클러스터 중심이 서로 멀리 떨어진 위치에서 시작하도록 설정
  • 첫번째 중심을 랜덤으로 선택한 후, 남은 중심들은 기존 중심들로부터 가장 멀리 떨어진 데이터 포인트를 선택한다.
  • 수렴 속도 향상과 성능 개선 효과를 가진다.

K-means의 한계

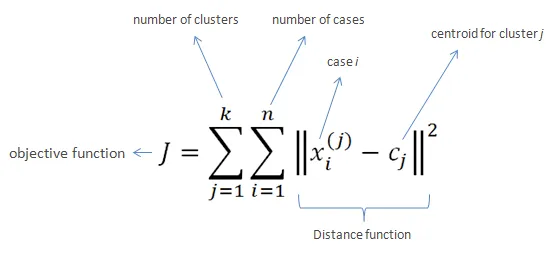
• 위의 그림은 k-means의 목적함수를 나타낸다.
• 한계
  • 초기화에 민감 : k-means는 초기화 방식에 따라 최종 결과가 달라질 수있다. (지역 최적값에 수렴하는 알고리즘임)
  • 클러스터 개수 k의 사전 설정 : 클러스터 개수 k를 사전에 설정해야한다. k를 잘못설정하면, 실제 데이터 구조를 반영하지 못할 수 있다.
  • 이상치에 민감 : 클러스터 중심과의 거리의 제곱합을 최소화 시키는 거리기반 알고리즘으로 이상치에 민감하다.
  • 계산량 증가 : 모든 데이터 포인트와 모든 클러스터 중심 간 거리를 반복적으로 계산하므로 데이터셋 크기가 커질수록 계산량이 크게 증가한다.
  • 클러스터 내부거리만 고려 : 목적함수가 클러스터 내부 거리만 고려하므로 클러스터 간의 거리를 고려하지 않는다. 서로다른 클러스터가 가까이 위치한다면 경계가 불명확해질 수 있다.

K-means 장단점

장점

• 알고리즘이 간단하고 큰 데이터에도 손쉽게 사용가능

단점 (목적 함수 한계와 연관)

• 연속형 변수에 가장 최적화 되어 있다.
• 결과가 초기에 지정한 클러스터 중심의 위치에 따라 달라질 수있어 반복이 필요하다.
• 클러스터의 개수 지정이 필요하다.
• 이상치에도 민감하다.
• 구형의 또는 비선형 구조를 클러스터링 할때는 성능이 떨어진다.
  

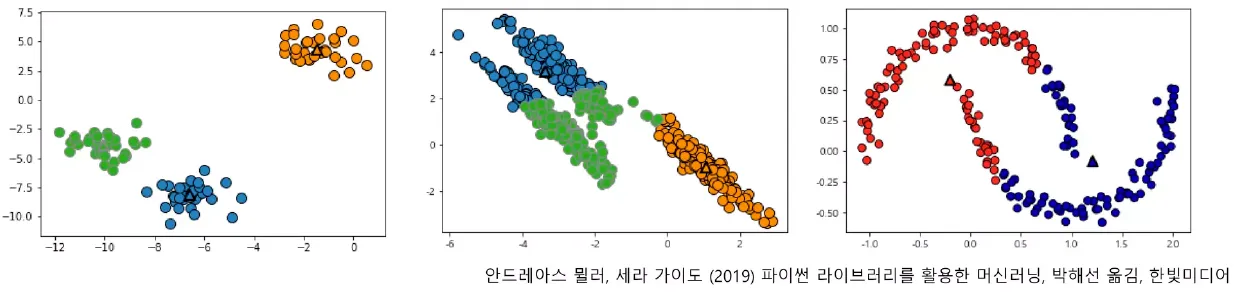
K 설정 및 군집 평가

K 설정

• 비즈니스 도메인 지식 확인이 필요하다.
  
• faeture 자체에 대해 어떤 데이터 패턴을 보이는지 시각화를 통해 미리 확인해보아야한다.
  • 차원축소, 다른 군집화를 사용

Elbow method

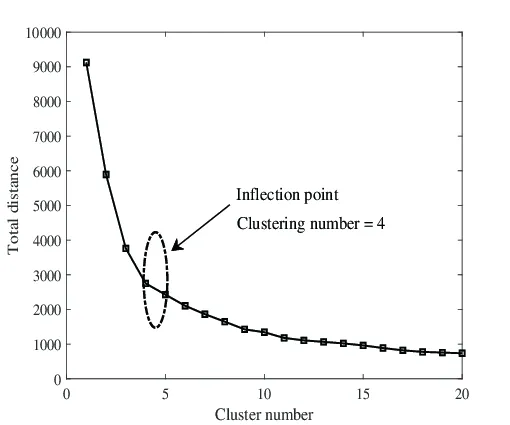
• 최적의 클러스터 개수(K)를 설정하기 위한 방법으로,거리 제곱합(J)을 가지고 클러스터의 품질과 최적의 K를 결정한다.
• 원리
  • K를 증가면 내부 포인트 간의 평균 거리가 줄어들어 J값이 감소한다.
  • K를 계속 증가시키면, J값의 감소 폭이 줄어드는 지점이 생긴다. 이를 Elbow Point라고 하며, 최적의 클러스터 개수로 간주한다.

군집 평가

외부 평가

• 클러스터링 결과를 참조 레이블(Groud Truth)와 비교하여 평가하는 방식이다.
• 레이블이 이미 있는 지도 학습용 데이터셋이 필요하다.
• 방법
  • Rand index (RI)
    • 데이터 포인트 간의 쌍을 기준으로, 투 클러스터링 결과가 얼마나 일치하는지를 계산
    • 데이터 포인트 쌍이 같은 클러스터에 있는 경우, 다른 클러스터에 있는 경우의 일치 여부를 통해 계산
    • 수식
      
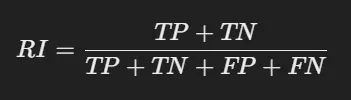
      • 분모는 전체 데이터 쌍의 수로 nC2로 계산됨
      • TP (True Positive): 참조와 평가에서 모두 같은 클러스터에 속한 데이터 쌍
      • TN (True Negative): 참조와 평가에서 모두 다른 클러스터에 속한 데이터 쌍
      • FP (False Positive): 참조에서는 다른 클러스터, 평가에서는 같은 클러스터에 속한 데이터 쌍
      • FN (False Negative): 참조에서는 같은 클러스터, 평가에서는 다른 클러스터에 속한 데이터 쌍
  • Adjusted Rand Index (ARI)
    • Rand Index를 확장하여, 두 클러스터링 간의 일치도를 측정하면서 무작위로 생성된 클러스터링 결과에서도 일관된 점수를 부여하도록 보정된 지표
    • 수식
      
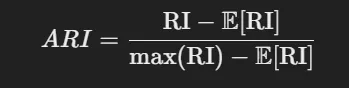
      • RI : Rand Index
      • E[RI] (Expected Rand Index) : 데이터를 무작위로 클러스터에 배정했을 때 예상되는 Rand Index
      • Max(RI) : Rand Index의 최대값으로 이론적으로 1로 계산된다.

내부 평가

• 참조 레이블 없이, 클러스터링 자체의 품질을 평가하는 방식이다.
• 클러스터링 결과만으로 평가가 가능하다.
• 실루엣 계수(Silhouette coefficient)
  
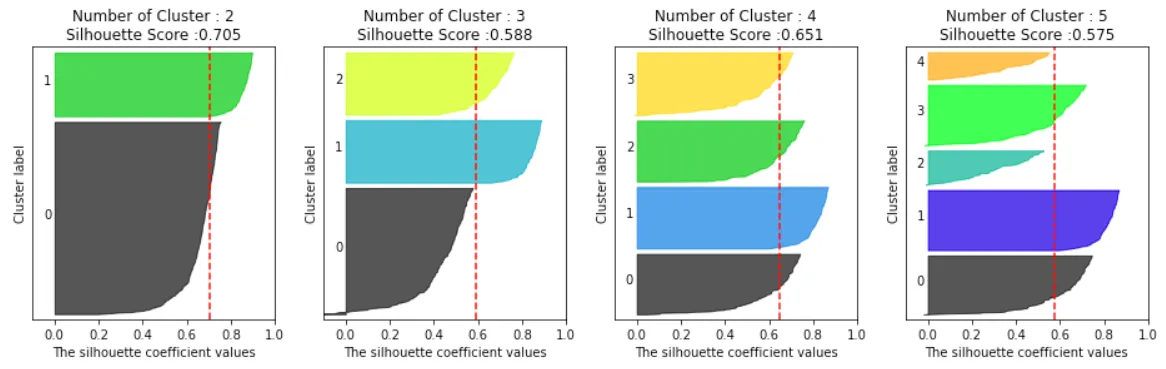
  • 클러스터 내부의 응집도와 클러스터 간의 분리도를 동시에 평가하는 지표이다.
  • 각 데이터 포인트가 자신이 속한 클러스터에 얼마나 잘 속해 있는지(응집도)를 측정하고, 동시에 다른 클러스터와 얼마나 잘 분리되어 있는지(분리도)를 평가한다.