KNN 알고리즘 실제 데이터에 적용하기

KNN 알고리즘을 적용하여 최적의 파라미터 찾기

💡 목표 : KNN 알고리즘을 Seaborn 예제 데이터셋 중 하나인 diamonds 데이터셋에 적용하기

• 거리 기반 알고리즘인 KNN 알고리즘을 사용하므로 수치형 데이터의 경우에 표준화가 필요하다.
• 범주형 데이터의 경우 원-핫 인코딩을 적용한다.

💡 왜 거리기반 알고리즘에 스케일링이 필요할까?

• 거리 기반 알고리즘은 일반적으로 유클리디안 거리(Euclidean Distance)나 맨하탄 거리(Manhattan Distance)를 사용한다.
• 거리 계산은 데이터의 크기와 단위에 따라 영향을 받는다. 즉, 값의 스케일이 큰 변수가 작은 변수보다 거리에 더 큰 영향을 미친다.
• 거리기반 알고리즘 예시 : K-Nearest Neighbors, K-means, DBSCAN, Hierachical Clustering 등

실습

라이브러리 불러오기

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, root_mean_squared_error
import matplotlib.pyplot as plt
import seaborn as sns

데이터 불러오기

diamonds = sns.load_dataset('diamonds')

• seaborn 데이터셋의 다이아몬드 데이터 불러오기

데이터 정보확인

diamonds.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 53940 entries, 0 to 53939
Data columns (total 10 columns):
 #   Column   Non-Null Count  Dtype   
---  ------   --------------  -----   
 0   carat    53940 non-null  float64 
 1   cut      53940 non-null  category
 2   color    53940 non-null  category
 3   clarity  53940 non-null  category
 4   depth    53940 non-null  float64 
 5   table    53940 non-null  float64 
 6   price    53940 non-null  int64   
 7   x        53940 non-null  float64 
 8   y        53940 non-null  float64 
 9   z        53940 non-null  float64 
dtypes: category(3), float64(6), int64(1)
memory usage: 3.0 MB

수치형 변수와 범주형 변수 확인

numerical_columns = diamonds.drop(columns=['price']).select_dtypes(include=['number']).columns
print("수치형 변수:")
print(numerical_columns)

categorical_columns = diamonds.select_dtypes(include=['category']).columns
print("문자열 변수:")
print(categorical_columns)

• 수치형 변수와 범주형 변수에 서로 다른 방법을 적용하여 전처리 해야하므로 각 컬럼을 가져온다.
  • 종속 변수인 price는 표준화에서 제외했다.

수치형 변수 표준화 적용

scaler = StandardScaler()
scaled_features = scaler.fit_transform(diamonds[numerical_columns])

diamonds[numerical_columns] = scaled_features

• 스케일링을 위해 수치형 변수에 표준화를 적용한다.
• 표준화란?
  • 데이터를 평균이 0, 표준편차가 1이 되도록 변환한다.

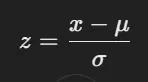
범주형 변수에 원-핫 인코딩 적용

diamonds = pd.get_dummies(diamonds, columns=categorical_columns, drop_first=True)

• 원핫 인코딩이란?
  • 범주를 고유한 이진 벡터로 변환하는 방법으로, 각 범주를 고유한 위치에 1을 할당하고 나머지는 0으로 설정하여 표현한다.
• (참고) 수치형 변수와 범주형 변수의 스케일 차이가 모델의 성능에 큰 영향을 미치지 않는 경우, 원-핫 인코딩한 결과에 수치형 변수와 함께 표준화를 적용할 필요가 없다.

독립변수, 종속 변수 분리

X = diamonds.drop('price', axis=1)
y = diamonds['price']

학습 테스트 데이터 나누기

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

K 값에 따른 모델 성능 변화 시각화 및 최적의 k 찾기

# K 값 범위 설정
k_values = range(1, 22, 2)

mse_values = []

for k in k_values:
  print(f'k 값 : {k}')
  model = KNeighborsRegressor(n_neighbors=k)
  model.fit(X_train, y_train)
  y_pred = model.predict(X_test)
  mse = mean_squared_error(y_test, y_pred)
  mse_values.append(mse)
  
# 시각화
plt.figure(figsize=(11, 6))
plt.plot(k_values, mse_values, marker='o', label="MSE")
plt.xticks(k_values)
plt.title('MSE vs K', fontsize=13)
plt.xlabel('K', fontsize=12)
plt.ylabel('Mean Squared Error', fontsize=12)
plt.grid()
plt.legend()
plt.show()

# 최적의 k 출력
optimal_k = k_values[np.argmin(mse_values)]
print(f'최적의 k값: {optimal_k}, 최소 MSE: {min(mse_values):.4f}')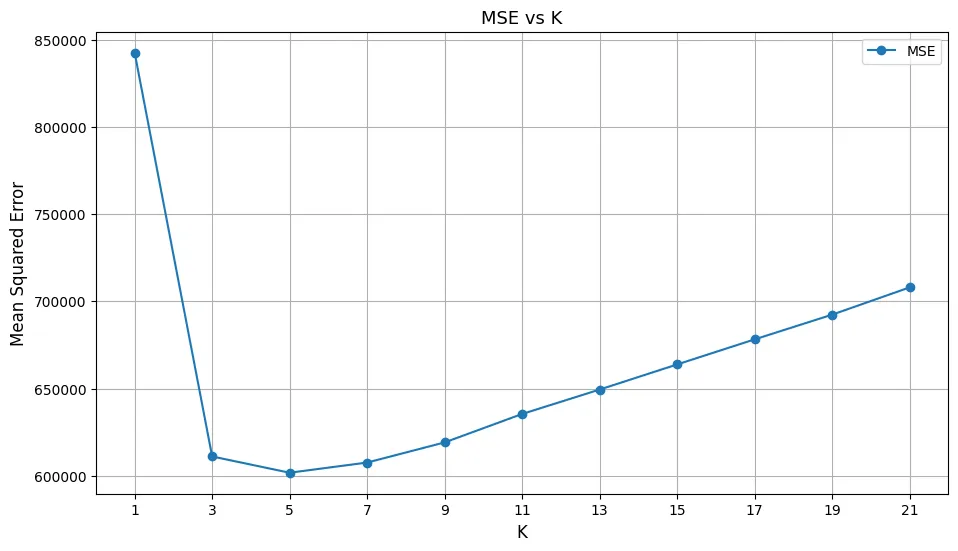

• (참고) 위 코드는 k 값에 따른 MSE 변화를 시각화하기 위해 test 데이터를 사용한 예제이다. 하지만 test 데이터는 모델의 최종 성능 평가를 위해 보관해야 하며, 이처럼 최적의 k 값을 찾는 과정에서는 교차 검증(Cross Validation)을 사용하는 것이 더 바람직하다.
  그

그리드 서치를 적용하여 최적의 하이퍼파리머터 찾기

param_grid = {
    'n_neighbors': np.arange(1, 10, 2),
    'weights':['uniform','distance'],
    'metric':['euclidean','manhattan']
}

knn = KNeighborsRegressor()

grid_search = GridSearchCV(estimator = knn, param_grid = param_grid, cv=5, scoring= 'neg_mean_squared_error', verbose=2)
grid_search.fit(X_train, y_train)

best_params = grid_search.best_params_
best_score = grid_search.best_score_

print(f'최적의 하이퍼 파라미터 {best_params}')
print(f'교차검증 Best_score :{best_score:.4f}')

• 그리드 서치를 적용하여 최적의 하이퍼파라미터를 찾을 수 있다.

• 참고로 그리드 서치에 mse 평가기준을 사용할때 neg_mean_squared_error를 사용해야한다.

  • 이유 : 그리드 서치는 점수가 큰 값을 찾기 때문이다.

  그리드 서치 결과 시각화

results = grid_search.cv_results_
mean_scores = results['mean_test_score']
std_scores = results['std_test_score']

k_values = [params['n_neighbors'] for params in results['params'] if params['weights']== best_params['weights'] and params['metric'] == best_params['metric']]

plt.figure(figsize=(10, 6))
plt.plot(k_values, mean_scores[:len(k_values)], marker='o', label='Mean Squared Error')
plt.fill_between(k_values, mean_scores[:len(k_values)] - std_scores[:len(k_values)],mean_scores[:len(k_values)] + std_scores[:len(k_values)],alpha=0.2)
plt.axvline(x= best_params['n_neighbors'], color='r',linestyle='--')
plt.legend()
plt.grid()
plt.show()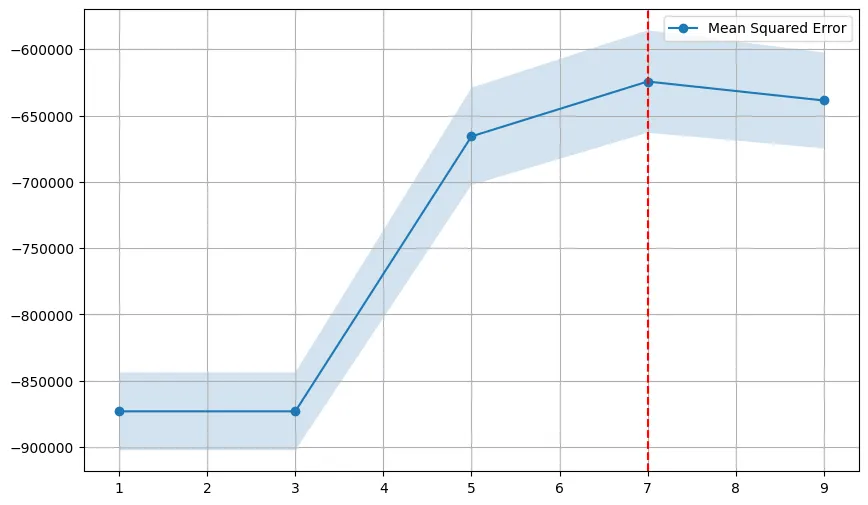

• fill_between: mean_scores의 평균값을 기준으로 상하 표준편차(std_test_score) 범위를 시각화하여 결과의 신뢰 구간을 표현한다.
• axvline : 최적의 하이퍼파라미터(n_neighbors) 값을 강조하기 위해 해당 x축 위치에 수직선을 표시한다.

최종 모델 학습 및 평가하기

best_knn=KNeighborsRegressor(**best_params)
best_knn.fit(X_train, y_train)
y_test_pred = best_knn.predict(X_test)

test_rmse = root_mean_squared_error(y_test,y_test_pred)
print(f'rmse:{test_rmse:.4f}')

• 최적의 파라미터를 가지고 최종 모델을 학습하여 test 데이터로 평가

KNN 알고리즘을 이용한 이상치 탐지

동작 순서

1. 거리 계산: 각 데이터 포인트에 대해 k개의 최근접 이웃과의 거리를 계산한다.
2. 거리 기준 이상치 판단:
   • 평균 거리 또는 k번째 이웃과의 거리가 임계값(threshold)을 초과하면 해당 데이터를 이상치로 간주한다.

💡 K-nearest neighbor, Nerest Neighbor 비교

• sklearn에서 제공하는 KNN과 NN이 존재하며 서로 다른 역할을 한다.

  특징	KNN	Nearest Neighbor
  목적	분류(Classification), 회귀(Regression)	거리 기반 분석, 이상치 탐지
  학습 유형	지도 학습(Supervised Learning)	비지도 학습(Unsupervised Learning)
  목표 변수 필요 여부	필요	불필요
  효율성	상대적으로 무거움	가볍고 효율적
  주 사용 사례	클래스 예측, 값 예측	거리 계산, 밀도 분석, 이상치 탐지

실습

라이브러리 불러오기

from sklearn.neighbors import NearestNeighbors
import seaborn as sns
import matplotlib.pyplot as plt

데이터 불러오기

data = sns.load_dataset('iris')

# 독립 변수만 가져오기
X = data.drop(columns="species")

• (참고) seaborn에서 제공하는 iris 데이터에는 일반적으로 이상치가 없이 잘 정제된 데이터셋이지만 실습을 위해 사용함

Nearest Neighbors를 이용한 이상 탐지 적용

n_neighbors = 5
nbrs = NearestNeighbors(n_neighbors=n_neighbors).fit(X)
distances, indices = nbrs.kneighbors(X)

avg_distances = distances.mean(axis=1)

threshold = np.percentile(avg_distances,95)
outlier_indices =np.where(avg_distances > threshold)[0]

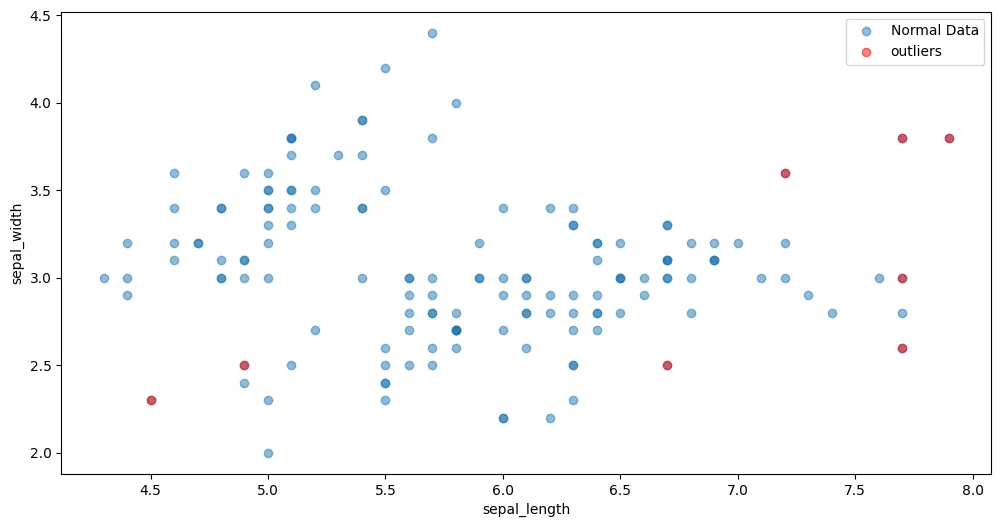
outliers_deteced = data.iloc[outlier_indices]

동작 순서

1. 최근접 이웃 탐색

• NearestNeighbors를 사용해 각 데이터 포인트의 5개의 최근접 이웃 거리(distances)와 인덱스(indices**)를 계산

2. 평균 거리 계산
   • 각 데이터 포인트에 대해 k개의 이웃과의 평균 거리(avg_distances)를 구함.
3. 임계값 설정
   • 평균 거리의 상위 5% 값을 임계값(threshold)로 설정
4. 이상치 탐지
   • 평균 거리가 임계값을 초과하는 데이터 포인트의 인덱스를 찾아(outlier_indices) 추출

이상치 탐지 탐지 결과 시각화

plt.figure(figsize=(12,6))
plt.scatter(data['sepal_length'],data['sepal_width'], label='Normal Data', alpha=0.5)
plt.scatter(outliers_deteced['sepal_length'],outliers_deteced['sepal_width'],color='r' , label='outliers', alpha=0.5)
plt.legend()
plt.xlabel('sepal_length')
plt.ylabel('sepal_width')
plt.show()