[MATLAB] 문제 해결하기 2/2

💡 도움이 되셨다면 ♡와 팔로우 부탁드려요! 미리 감사합니다.

💡 MATLAB을 이용하여 함수를 정의하고 그래프를 그려보며 다양한 수학 문제들을 해결할 수 있다.

퇴사 시 누적 소득세, 저축액 계산하기

당신은 28세에 A사에 입사하여 55세까지 근무하게 되며, 처음 입사 시 연봉은 X원입니다. 연봉은 매년 3%씩 증가한다고 가정합니다. 아래의 소득세율 표에 따라 매년 소득세를 납부하며, 소득공제는 없는 것으로 합니다.

과세 표준 구간	세율
1,200만 원 이하	6%
1,200만 원 초과 ~ 4,600만 원 이하	72만 원 + 1,200만 원 초과분의 15%
4,600만 원 초과 ~ 8,800만 원 이하	582만 원 + 4,600만 원 초과분의 24%
8,800만 원 초과 ~ 1억 5천만 원 이하	1,590만 원 + 8,800만 원 초과분의 35%
1억 5천만 원 초과	3,760만 원 + 1억 5천만 원 초과분의 38%

1번 문제 (누적 소득세)

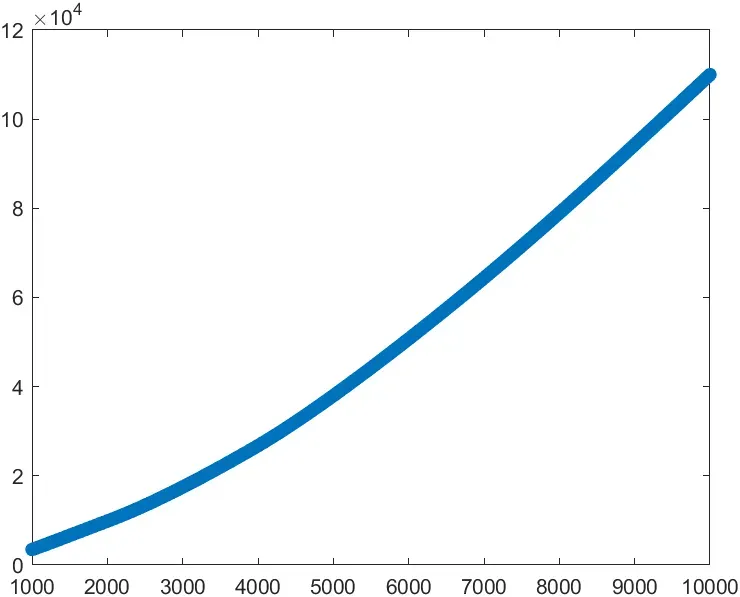
과세 표준 구간을 참고하여 당신의 총 연봉에 대해 55세까지 납부하게 될 세금 총액을 계산하는 함수를 작성해 보세요. 이 함수는 연봉을 입력받아 55세까지의 누적 세금을 반환해야 합니다. 즉, g(초봉)=퇴사 시 누적 세금을 반환하는 함수입니다.

단, 연봉은 1,000만 원에서 1억 원 사이의 값을 가질 수 있으며, 10만 원 단위로 계산합니다. 예를 들어, 연봉은 1,000만 원, 1,010만 원, ..., 2억 원으로 설정하며, 계산 시 만 원 단위는 생략합니다.

정답 예시

• initial_salary부터 current_salary를 3%씩 증가시키며 매년 소득세를 계산하고 누적합니다.
• 연봉 구간에 따라 세율을 적용하여 매년 소득세(annual_tax)를 구하고 이를 누적 세금(total_cumulative_tax)에 더합니다.
• 초기 연봉과 퇴사 시까지의 누적 세금을 저장한 후, 연봉 대비 누적 세금을 그래프로 시각화합니다

cumulative_tax_data = [];
for initial_salary = 1000:10:10000
    current_salary = initial_salary;
    total_cumulative_tax = 0;
    for age = 28:55
        if current_salary <= 1200
            annual_tax = current_salary * 0.06;
        elseif current_salary <= 4600
            annual_tax = 72 + (current_salary - 1200) * 0.15;
        elseif current_salary <= 8800
            annual_tax = 582 + (current_salary - 4600) * 0.24;
        elseif current_salary <= 15000
            annual_tax = 1590 + (current_salary - 8800) * 0.35;
        else
            annual_tax = 3760 + (current_salary - 15000) * 0.38;
        end
        total_cumulative_tax = total_cumulative_tax + annual_tax;
        current_salary = current_salary * 1.03;
    end
    cumulative_tax_data = [cumulative_tax_data; initial_salary total_cumulative_tax];
end

plot(cumulative_tax_data(:, 1), cumulative_tax_data(:, 2), 'o');

2번 문제 (누적 저축액)

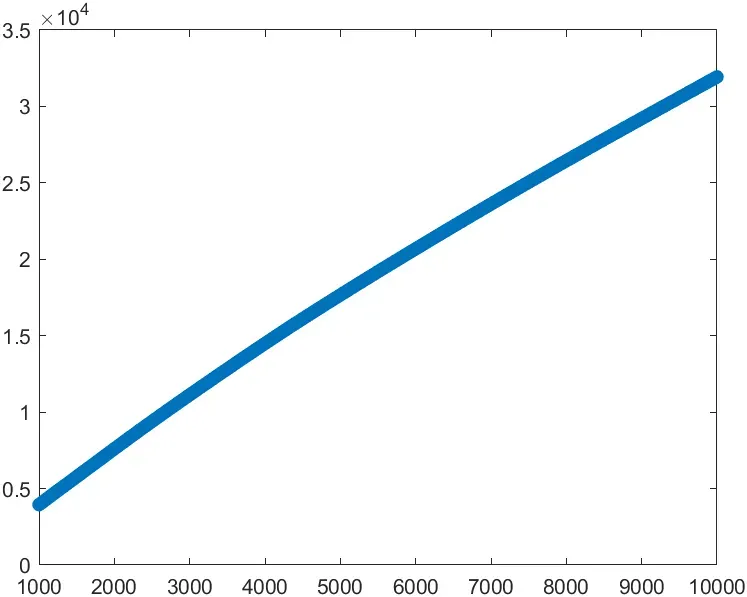
당신은 매년 세금을 제외한 연봉의 10%를 저축한다고 가정합니다.

이자율은 고려하지 않습니다. 그렇다면, 퇴사 시까지 저축한 총액은 얼마일까요? 이를 초봉에 따른 함수로 그래프를 그리는 M-file을 작성하세요. 즉, f(초봉)=총 저축액을 반환하는 함수입니다.

정답 예시

• initial_salary를 시작으로 매년 연봉 3% 증가, 세금 공제 후 남은 연봉의 10%를 저축합니다.
• 누적 저축(accumulated_savings)을 계산하고 초기 연봉에 따라 그래프로 표시합니다.
• 결과는 초기 연봉과 저축 총액의 관계를 시각화하여 보여줍니다.

total_savings_data = [];
for initial_salary = 1000:10:10000
    salary = initial_salary;
    accumulated_savings = 0;
    for age = 28:55
        if salary <= 1200
            income_tax = salary * 0.06;
        elseif salary <= 4600
            income_tax = 72 + (salary - 1200) * 0.15;
        elseif salary <= 8800
            income_tax = 582 + (salary - 4600) * 0.24;
        elseif salary <= 15000
            income_tax = 1590 + (salary - 8800) * 0.35;
        else
            income_tax = 3760 + (salary - 15000) * 0.38;
        end
        accumulated_savings = accumulated_savings + (salary - income_tax) * 0.1;
        salary = salary * 1.03;
    end
    total_savings_data = [total_savings_data; initial_salary accumulated_savings];
end

plot(total_savings_data(:, 1), total_savings_data(:, 2), 'o')

가우스 소거법, 가우스-조던 소거법

1번 문제 (REF)

가우스 소거법을 적용하여 Row Echelon Form (REF) 구하기

1. 행 교환하기 (피벗 위치가 0일 때)
2. 행에 다른 행의 배수를 더해 피벗 아래의 모든 값을 0으로 만들기

💡 REF의 조건

1. 각 행의 피벗 값은 해당 행의 첫 번째 0이 아닌 원소여야 한다.
2. 피벗 아래에 있는 모든 원소는 0이어야 한다.
3. 피벗은 행 아래로 갈수록 오른쪽에 위치해야 한다.
4. 모든 0으로만 이루어진 행은 행렬의 가장 아래에 위치해야 한다.

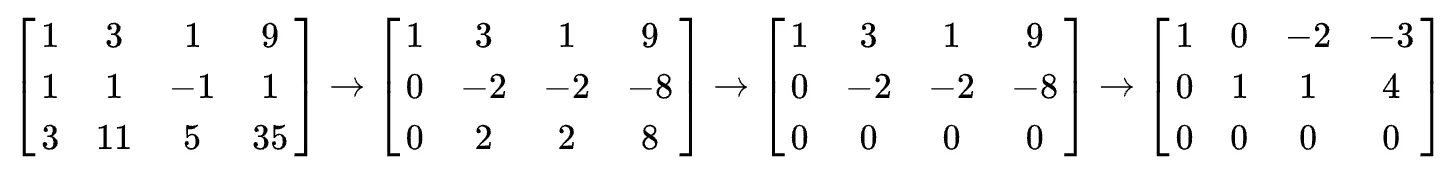
function U = GE(A)
    [n, m] = size(A);
    
    for i = 1:min(n, m)
        % 1. 현재 피벗이 0이라면 행 교환 수행
        if A(i, i) == 0
            swapped = false;
            for j = i+1:n
                if A(j, i) ~= 0
                    % 행 교환
                    temp = A(i, :);
                    A(i, :) = A(j, :);
                    A(j, :) = temp;
                    swapped = true;
                    break;
                end
            end
            % 교환할 수 있는 행이 없는 경우, 다음 열로 넘어감
            if ~swapped
                continue;
            end
        end
        
        % 2. 현재 피벗 열 아래의 모든 원소를 0으로 만들기 위해서 현재 피벗 행의 배수를 빼줌
        for k = i+1:n
            if A(i, i) ~= 0
                factor = A(k, i) / A(i, i);
                A(k, :) = A(k, :) - factor * A(i, :);
            end
        end
    end
    U = A;
end

2번 문제 (RREF)

가우스-조던 소거법을 적용하여 Reduced Row Echelon Form (RREF) 구하기

1. 행 교환하기 (피벗 위치가 0일 때)

   두 행의 위치를 서로 바꿔서 0이 아닌 값이 피벗 위치에 오도록 합니다.

2. 행을 상수로 곱하기 (피벗 요소를 1로 만들 때)

   한 행의 모든 값에 0이 아닌 상수를 곱하여 피벗 요소를 1로 만듭니다.

3. 행에 다른 행의 배수를 더하기 (위 아래 요소를 0으로 만들 때)

   한 행에 다른 행의 상수 배를 더해 특정 위치의 값을 0으로 만듭니다.

💡 RREF의 조건

1. 피벗 값이 1이어야 한다.
2. 각 피벗은 해당 행의 첫 번째 1이 아닌 원소여야 한다.
3. 각 피벗이 있는 열에서는 그 외의 모든 원소가 0이어야 한다.
4. 모든 0이 아닌 행이 위에서 아래로 순서대로 정렬되어 있어야 하며, 아래에 있는 피벗의 열은 위에 있는 피벗의 열보다 오른쪽에 있어야 한다.

정답 예시

function U = GE2(A)
    [n, m] = size(A);

    for i = 1:min(n, m)
        % 1. 현재 피벗이 0이라면 행 교환 수행
        if A(i, i) == 0
            swapped = false;
            for j = i+1:n
                if A(j, i) ~= 0
                    % 행 교환
                    temp = A(i, :);
                    A(i, :) = A(j, :);
                    A(j, :) = temp;
                    swapped = true;
                    break
                end
            end
            % 교환할 수 있는 행이 없는 경우, 다음 열로 넘어감
            if ~swapped
                continue;
            end
        end

        % 2. 피벗 행을 나눠서 피벗 요소를 1로 만들기
        A(i, :) = A(i, :) / A(i, i);

        % 3. 다른 행에 현재 피벗 행의 배수를 빼줌
        for k = 1:n
            if k ~= i
                factor = A(k, i);
                A(k, :) = A(k, :) - factor * A(i, :);
            end
        end
    end
    U = A;
end

3번 문제 (행렬식)

가우스 소거법을 이용한 행렬식 구하기

1. n×n 정사각 행렬 A를 준비하고, 소거 과정을 진행합니다.
2. 피벗 행을 설정하고 가우스 소거법으로 삼각 행렬로 변환합니다. (행 교환 시 부호 조정)
3. 대각선 원소들의 곱을 계산하여 행렬식을 구합니다

정답 예시

가우스 소거법을 모두 적용한 이후 대각선 원소들을 곱해주는 방법

function det_A = GE_det(A)
    [n, m] = size(A);

    % A가 정사각행렬인지 확인
    if n ~= m
        error('Input must be a square matrix');
    end

    count_row_exchange = 0;  % 행 교환 횟수

    for i = 1:n
        % 1. 현재 피벗이 0이라면 행 교환 수행
        if A(i, i) == 0
            swapped = false;
            for j = i+1:n
                if A(j, i) ~= 0
                    % 행 교환
                    count_row_exchange = count_row_exchange + 1;
                    temp = A(i, :);
                    A(i, :) = A(j, :);
                    A(j, :) = temp;
                    swapped = true;
                    break
                end
            end
            % 만약 교환이 이루어지지 않고 피벗이 0인 경우 행렬식을 0으로 반환
            if ~swapped
                det_A = 0;
                return
            end
        end

        % 2. 현재 피벗 행을 기준으로 나머지 행을 소거
        for k = i+1:n
            factor = A(k, i) / A(i, i);
            A(k, :) = A(k, :) - factor * A(i, :);
        end
    end

    % 대각선 원소 곱 계산
    det_A = 1;
    for i = 1:n
        det_A = det_A * A(i, i);  % 대각선 원소를 곱함
    end

    % 행 교환 횟수가 홀수번이면 -1을 곱해줌
    if mod(count_row_exchange, 2) ~= 0
        det_A = det_A * -1;
    end
end

가우스 소거법을 진행하는 도중에 피벗을 곱해주는 방법

function det_A = GE_det2(A)
    [n, m] = size(A);

    % A가 정사각행렬인지 확인
    if n ~= m
        error('Input must be a square matrix');
    end

    det_A = 1;  % 초기 행렬식 값
    count_row_exchange = 0;

    for i = 1:n
        % 1. 현재 피벗이 0이라면 행 교환 수행
        if A(i, i) == 0
            swapped = false;
            for j = i+1:n
                if A(j, i) ~= 0
                    % 행 교환
                    count_row_exchange = count_row_exchange + 1;
                    temp = A(i, :);
                    A(i, :) = A(j, :);
                    A(j, :) = temp;
                    swapped = true;
                    break;
                end
            end
            % 만약 교환이 이루어지지 않고 피벗이 0인 경우 행렬식을 0으로 반환
            if ~swapped
                det_A = 0;
                return
            end
        end

        % 2. 행렬식을 구하기 위해 현재 행의 피벗을 곱해줌
        det_A = det_A * A(i, i);

        % 3. 다른 행에 현재 피벗 행의 배수를 빼줌
        for k = i+1:n
            factor = A(k, i) / A(i, i);
            A(k, :) = A(k, :) - factor * A(i, :);
        end
    end
    % 행 교환 횟수가 홀수번이면 -1을 곱해줌
    if mod(count_row_exchange, 2) ~= 0
        det_A = det_A * -1;
    end
end

4번 문제 (역행렬)

가우스-조던 소거법을 이용한 역행렬 반환하기

1. 초기 상태
   • 단, 정사각 행렬이 아닌 경우 종료
   
2. 가우스-조던 소거법 적용
   • 단, 특이 행렬인 경우 종료
3. 최종 결과
   

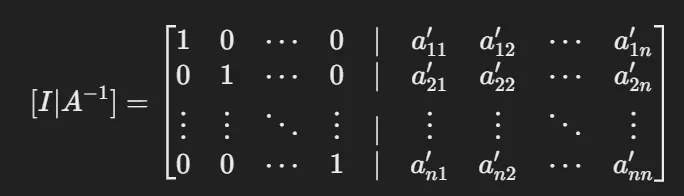
정답 예시

function invA = GE_inverse(A)
    [n, m] = size(A);

    % A가 정사각행렬인지 확인
    if n ~= m
        error('Input must be a square matrix');
    end

    % 확장 행렬 [A | I] 생성
    A = [A eye(n)];

    for i = 1:n
        % 1. 현재 피벗이 0이라면 행 교환 수행
        if A(i, i) == 0
            swapped = false;
            for j = i+1:n
                if A(j, i) ~= 0
                    % 행 교환
                    temp = A(i, :);
                    A(i, :) = A(j, :);
                    A(j, :) = temp;
                    swapped = true;
                    break
                end
            end
            % 교환 실패 시 행렬이 특이행렬임을 알림
            if ~swapped
                error('Matrix is singular and cannot be inverted');
            end
        end

        % 2. 피벗 행을 나눠서 피벗 요소를 1로 만들기
        A(i, :) = A(i, :) / A(i, i);

        % 3. 다른 행에 현재 피벗 행의 배수를 빼줌
        for k = 1:n
            if k ~= i
                factor = A(k, i);
                A(k, :) = A(k, :) - factor * A(i, :);
            end
        end
    end

    % 오른쪽 부분이 역행렬
    invA = A(:, n+1:end);
end