함수 그리기

Quiver()

• 속도 벡터를 점 (x, y)에 성분 (u, v)를 갖는 화살표로 표시하는 함수

형태

quiver(X, Y, U, V)

• X, Y: 화살표의 시작 위치(좌표) 행렬
• U, V: 각 지점에서 벡터의 x와 y 방향 성분

예시

[x, y] = meshgrid(0:0.2:2, 0:0.2:2);
u = cos(x).*y; v = sin(x).*y;
quiver(x, y, u, v)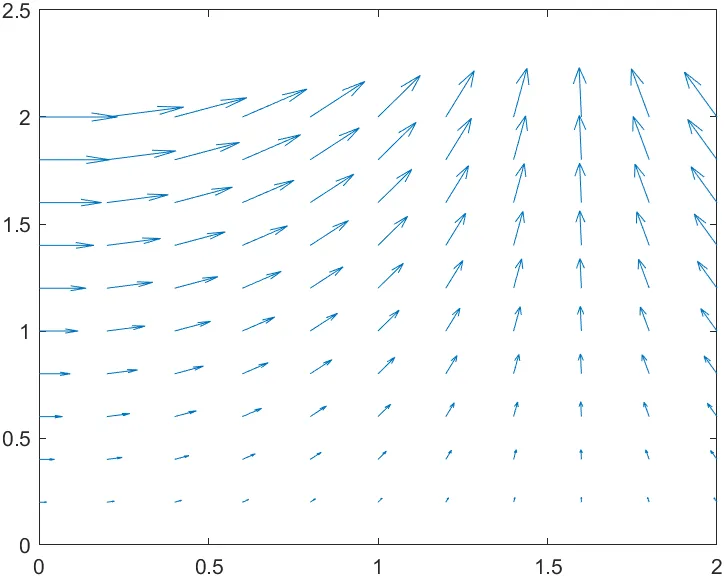

gradient()

• 행렬 Z에 x, y 성분의 수치적 기울기를 반환한다.
• quiver() 함수와 함께 사용하면 각 지점의 변화 방향과 크기를 화살표로 나타낼 수 있다.

형식

[DX, DY] = gradient(Z, dx, dy)

• Z: 2D 데이터 행렬.
• dx: x방향의 샘플 간격
• dy: y방향의 샘플 간격
• DX: x방향(열 방향)의 기울기(gradient)
• DY: y방향(행 방향)의 기울기(gradient)

예시

[X, Y] = meshgrid(-2:.2:2);
Z = X.*exp(-X.^2 - Y.^2);
[DX, DY] = gradient(Z, .2, .2);
quiver(X, Y, DX, DY)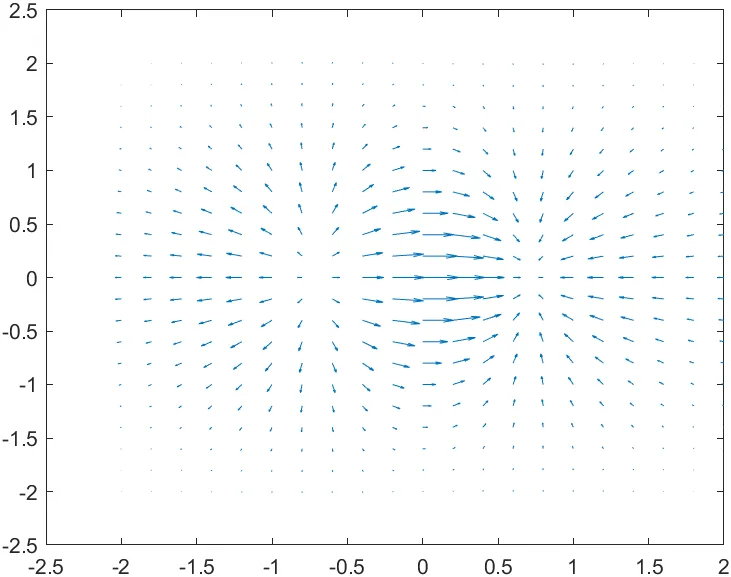

surf 그래프와 비교

[X, Y] = meshgrid(-2:.2:2);
Z = X.*exp(-X.^2 - Y.^2);
surf(X, Y, Z)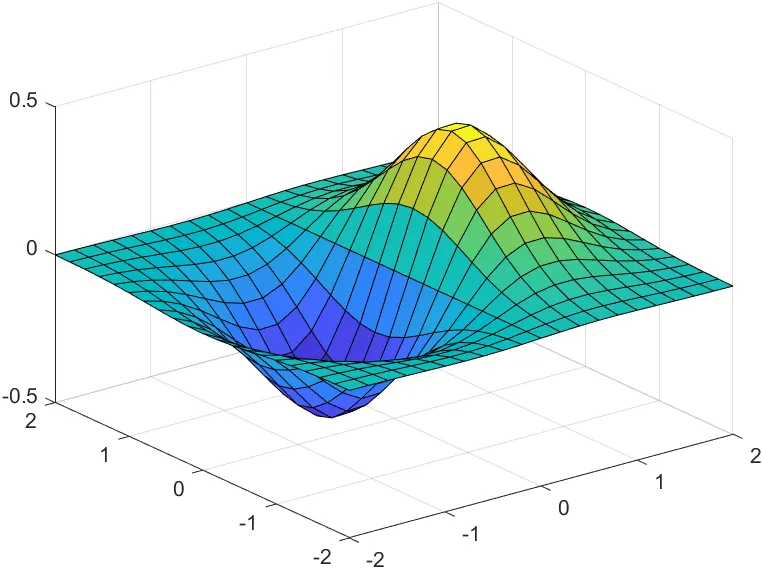

• surf 그래프에서 각 지점에서의 기울기의 크기와 방향을, x, y 그리드 좌표에 대한 gradient로 계산하여 시각화한 것이 quiver 그래프이다

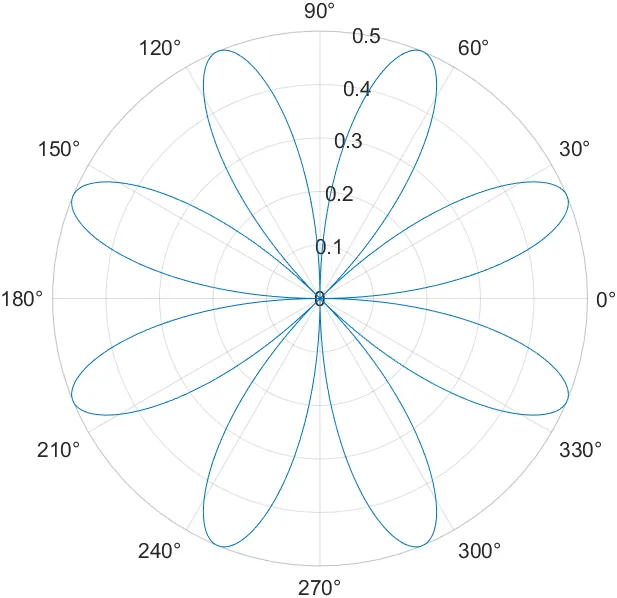
polarplot()

• 극 좌표에 대한 선 그래프 그리는 함수이다.

형식

polarplot(theta, r)

• theta : 각도(극 좌표의 θ, 라디안 단위)
• r : 반지름 (극 좌표의 r 값)

예시

theta = 0:0.01:2*pi;
rho = sin(2 * theta).*cos(2*theta);
polarplot(theta, rho)