이 블로그글은 2019년 조재영(Kevin Jo), 김승수(SeungSu Kim)님의 딥러닝 홀로서기 세미나를 수강하고 작성한 글임을 밝힙니다.
💡 도움이 되셨다면 ♡와 팔로우 부탁드려요! 미리 감사합니다.
Overfitting, Regularization
MLP의 문제점
Model Capacity
- Regression을 위해 다음과 같은 함수를 정의했다고 생각하자
둘의 차이가 무엇일까?
- 파라미터 개수 :2개
- 파라미터 개수 : 4개
파라미터 개수를 늘릴 수록 더 복잡한 현상들을 예측할 수 있음
→ 이러한 파라미터 개수를 model capacity라고 한다.
MLP의 경우 복잡한 현상들을 잘 예측하려면 model capacity를 늘려야한다.
- layer를 추가한다.
- 하나의 layer의 hidden unit을 늘린다.
→ model capacity를 무한정 늘리면 즉 파라미터를 계속 늘리면 성능이 무조건 좋아지지않을까? - overfitting
Overfitting
- model capacity가 늘어나면 train 데이터셋은 아주 잘 맞추지만 Test 데이터셋 (처음보는 데이터)에 대해서는 성능이 매우 낮아진다.
- 머신러닝의 목표 : 일반화
→ Overfitting (모델이 훈련 데이터에 지나치게 적합하게 학습하는 현상)
💡 일반화
- 학습된 모델이 새로운, 보지 못한 데이터에서도 높은 성능을 발휘하는 능력
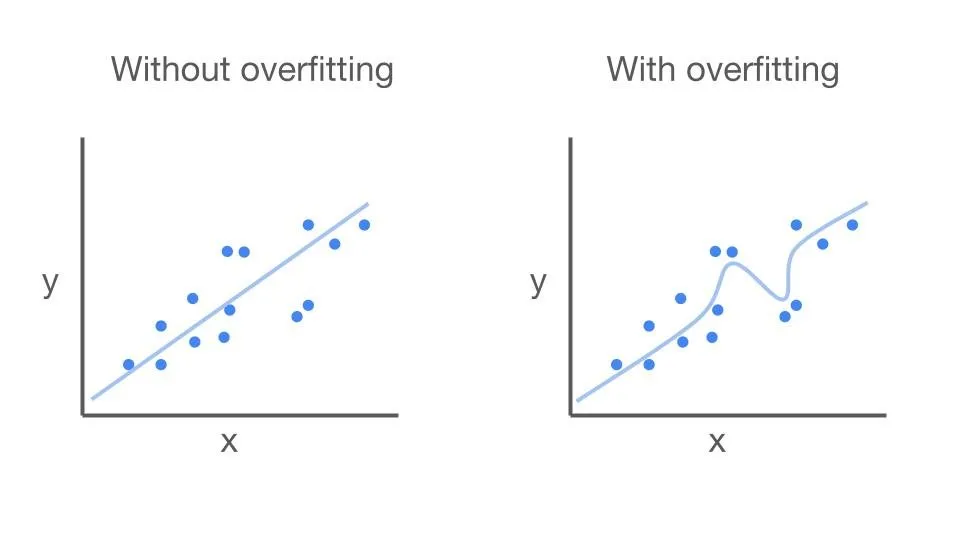
이미지 출처 : https://crunchingthedata.com/regression-overfitting/
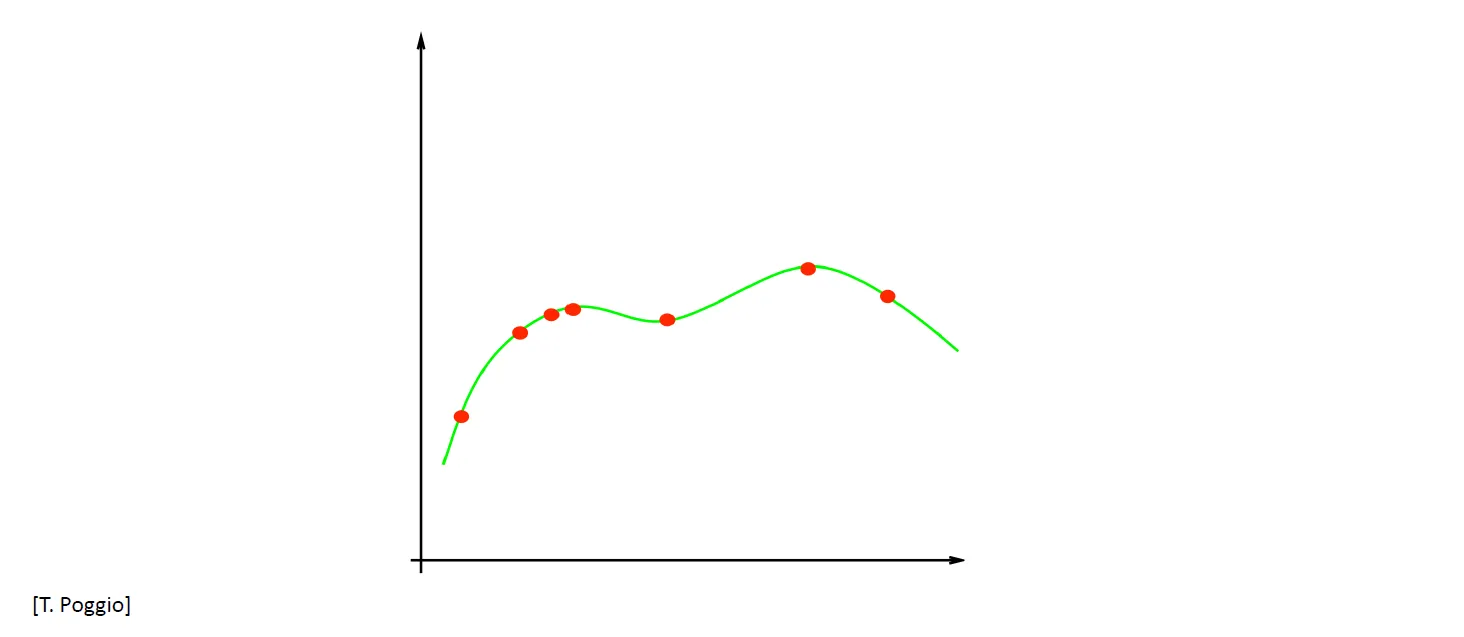
실제 전체 데이터 셋을 그린 그래프
- 빨간 색 점에 해당하는 데이터들을 가지고 학습을 하게 될 것임
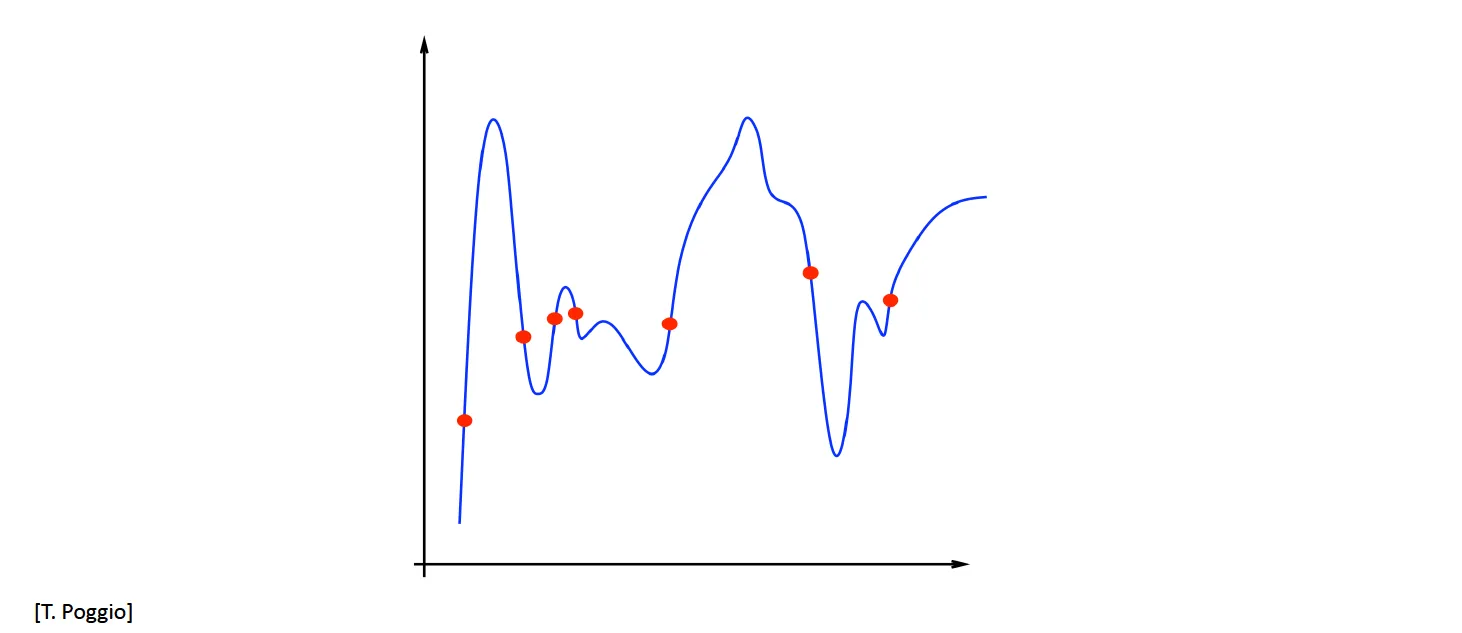
model capacity가 큰 모델로 학습한 그래프
- 오래 학습을 시키면 다음과 같은 그래프로 나타남
→ 실제 Test 데이터셋이 들어오는 경우 에러가 엄청나게 큼
Emprical Risk가 매우작은데 True Risk가 큰 경우 (Risk에 대한 설명은 아래에 있음)
💡True Risk vs Empirical Risk
True Risk
- 전체 모집단에 적용했을 때 학습 알고리즘의 예상 손실을 의미
→ 사실 True Risk를 줄이는 것이 목표가 되어야 함
but. 구할 수 없음
Empirical Risk
- 학습 알고리즘이 유한한 데이터 샘플(훈련 세트)에서 계산된 평균 손실을 의미
- 우리가 구할 수 있는 값
→ True Risk를 잘 표현해줄 수 있는 데이터 샘플을 골라 Empirical Risk를 줄여나감
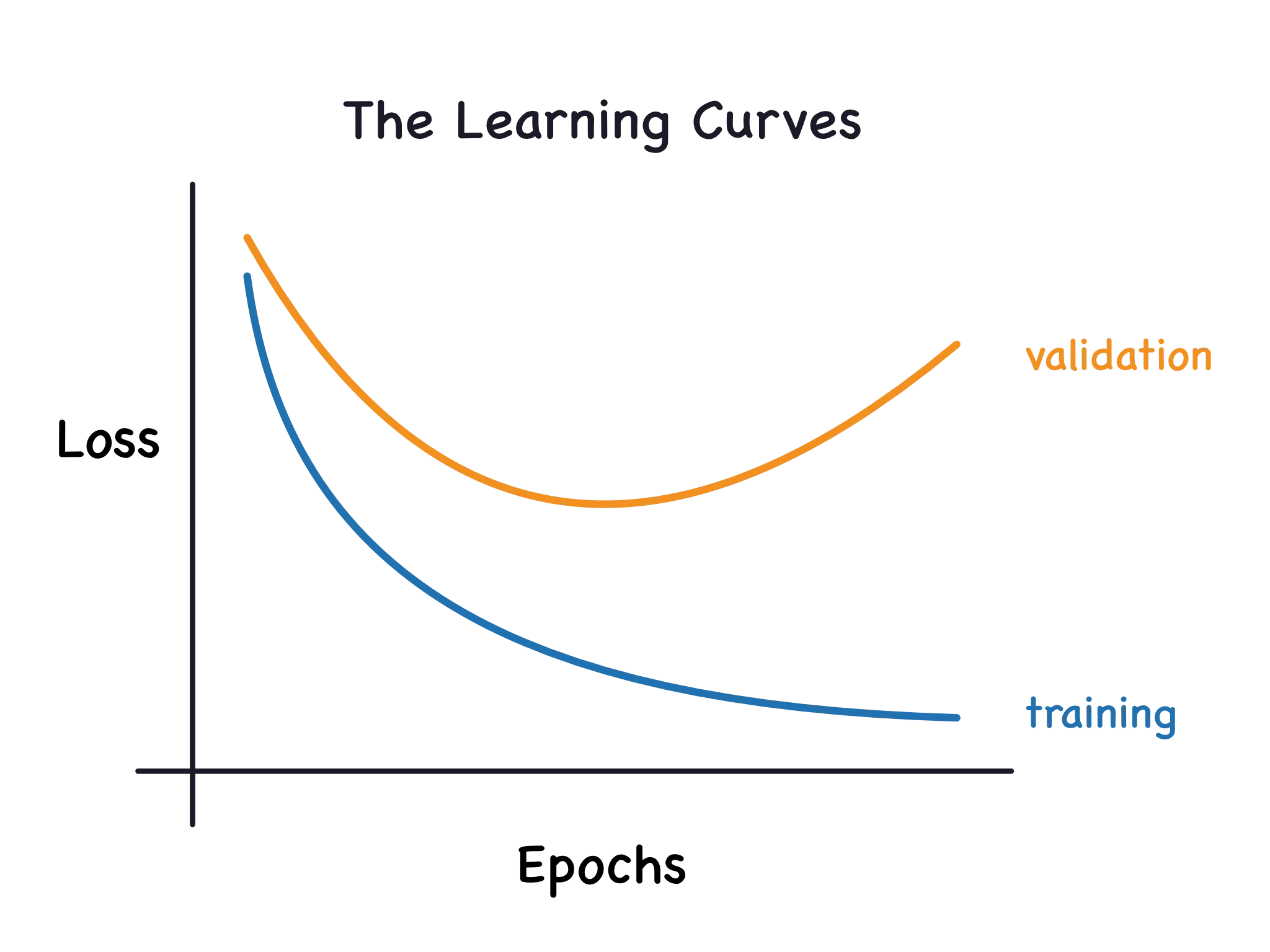
Loss Graph
- trainning loss와 validation loss가 같이 줄다가 validation loss가 커지는 경우
- overfitting이 일어났다고 함 (학습 데이터를 외워버림)
→ 적절히 학습을 끊어주는 것과 적절한 model capacity를 찾아서 overfitting의 문제를 해결 할 수 있다.
Regularizations
- overfitting을 해결하는 한 가지 방법
L2 Regularization
- 릿지 규제라고 함
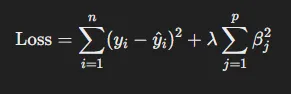
- L2 Regularization 항 구성
- λ : 정규화 강도를 조절하는 하이퍼파라미터
- 가중치 norm 값 : 파라미터의 크기가 너무 커지지 않도록 제한함
→ 왜 L2 Regularization 항이 overfitting을 줄여주는가?
기하학적 설명
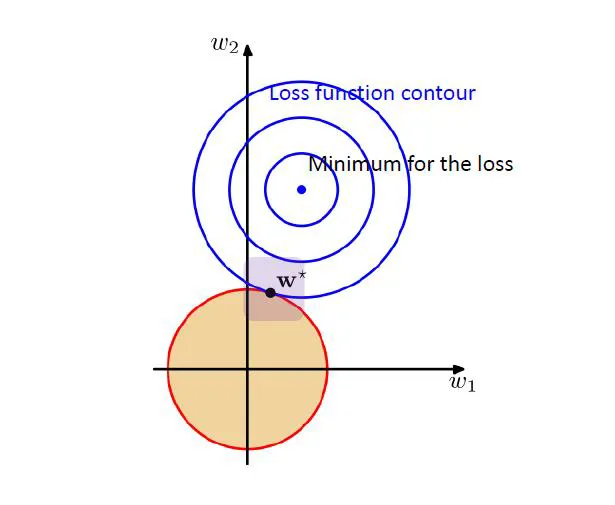
- w1과 w2라는 두 가지의 파라마터만 가지고 있는 모델을 가지고 있다고 하자.
- 어떤 특정 Train 데이터셋에 대해서 훈련시켰다.
- Train 데이터셋에 대한 global minimum이 어디간에 존재할것이다.
- regularization을 추가하면 이것에 대한 loss surpace가 생길 것임
- train의 loss surpace와 합쳐지게 됨
→ 학습 데이터의 loss minimum에 빠지지 않고 그 사이 어딘가로 학습하게 함 (학습 데이터의 손실 최소값에 지나치게 맞춰지는 것을 방지)
💡 Loss function contour
- 모델의 손실 함수가 특정 값들을 가질 때의 등고선을 나타낸 그래프
- 손실 함수의 출력이 일정한 점들의 집합을 시각화한 것으로, 손실 함수의 형태와 경사 정보를 제공한다.
- 같은 등고선에 있는 점들은 손실 함수의 값이 동일한 점들의 집합을 나타낸다.
- 등고선의 중심은 Global minimum이거나 Local minimum일 수 있다.
주로 2차원에서 모델의 매개변수(예: 가중치)가 손실에 미치는 영향을 시각적으로 분석할 때 사용
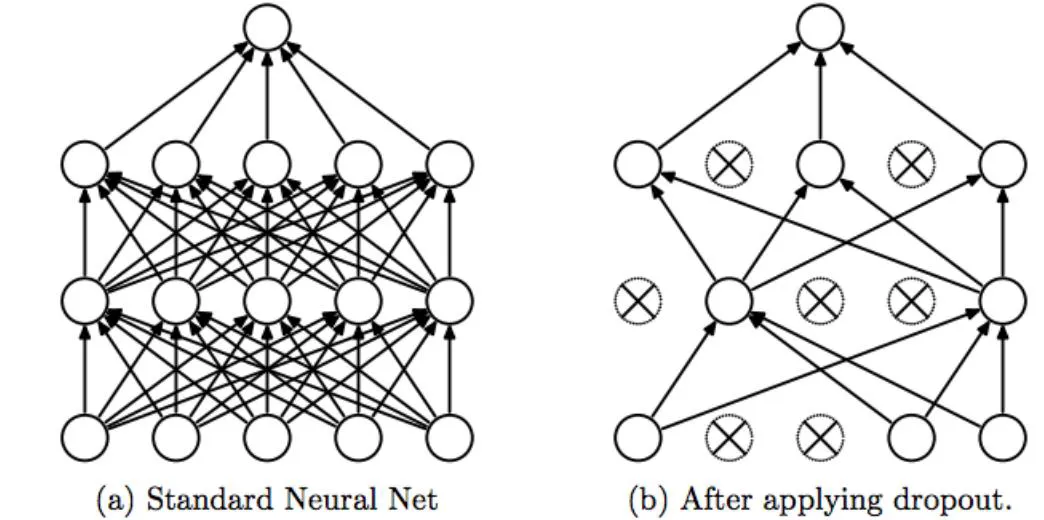
Dropout
- 학습과정에서 P(0~1)의 확률로 각각의 node를 꺼버리는 것 (가중치를 0으로 만듦)
- 기능
- 파라미터를 강제적으로 줄여서 general하게 예측하도록 학습함
- 남은 뉴런들이 보다 중요한 정보만 처리하게 되어 효율적 사용이 가능
- 복잡한 하나의 모델로 예측하기 보다는 간단한 여러가지 모델로 예측하고 결과를 합쳐서 사용 (앙상블)
💡 참고
- Validation과 Test시에는 Dropout이 적용되지 않음
- pytorch의 경우
model.eval()호출시 Dropout이 비활성화됨
Gradient Vanishing
- Gradient vanishing은 신경망 학습 중에 역전파 과정에서 gradient값이 점점 작아져, 앞쪽 층들에서 가중치가 거의 업데이트되지 않는 현상
- 이로 인해 깊은 네트워크에서는 학습이 어려워질 수 있다

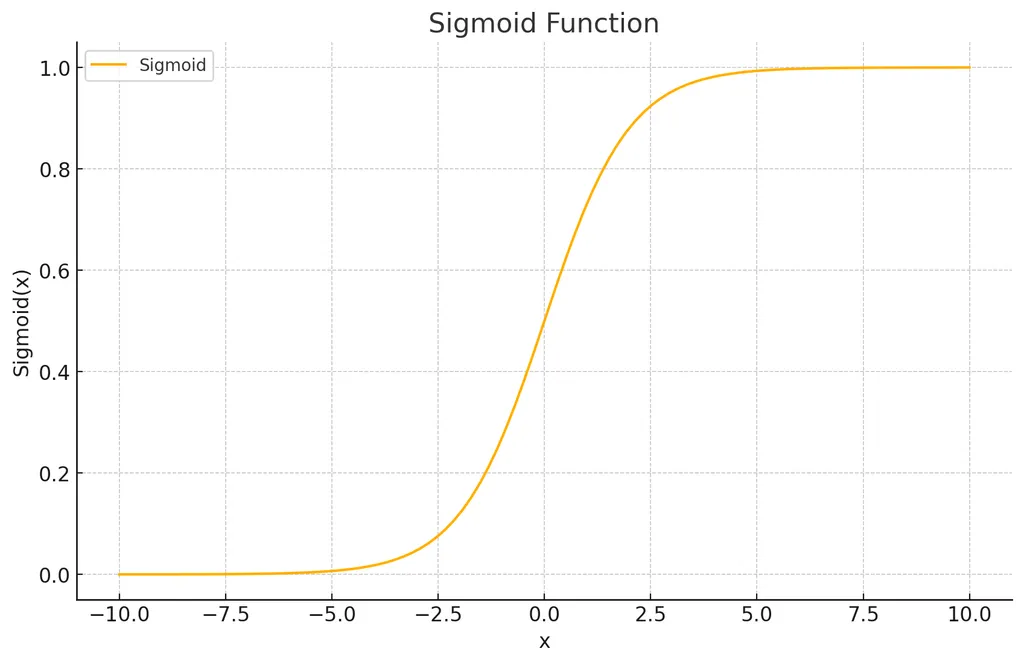
Sigmoid Activation
- 입력값이 매우 크거나 작을 때 출력이 0 또는 1에 가까워지면서 미분값이 거의 0에 수렴한다.
- 역전파 시 기울기를 계산할 때 이 작은 미분값이 계속 곱해지면서, 앞쪽 층으로 갈수록 기울기가 작아져서 가중치가 거의 업데이트되지 않게 되어 gradient vanishing이 발생한다.
→ 실제로, 1980년대에 역전파 알고리즘이 개발되었음에도 잘 사용되지 않았던 이유이다.
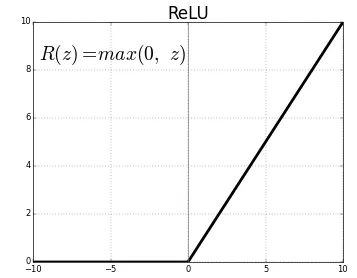
ReLU Activation
- ReLU를 사용하여 Sigmoid 의 문제를 해결함
- 0 보다 큰 경우에는 gradient가 잘 전달이 됨
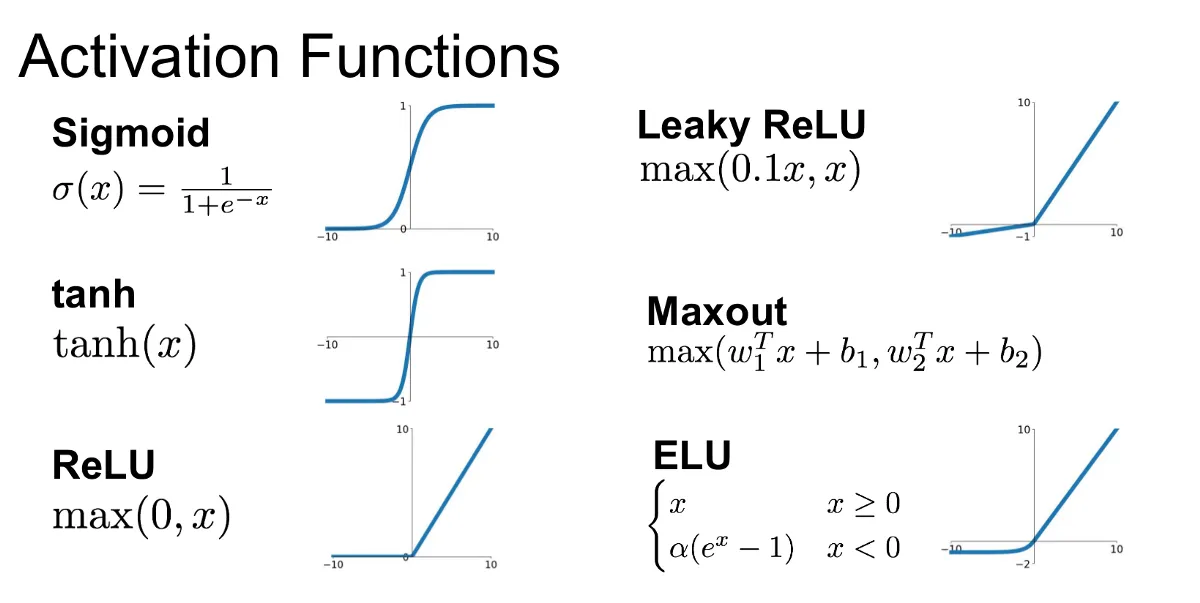
💡 Activation Example
Sigmoid: 값이 0과 1 사이로 압축되며, 이진 분류에 자주 사용됨tanh: 값이 -1에서 1 사이로 출력되어, Sigmoid보다 중심을 0으로 맞추는 효과가 있음ReLU: 0보다 작은 값은 0으로, 그 외는 그대로 출력하여 학습 속도를 가속화함Leaky ReLU: ReLU와 유사하지만, 음수 입력에 작은 기울기를 적용하여 죽은 뉴런 문제를 완화함Maxout: 여러 선형 함수 중 가장 큰 값을 선택하는 방식으로, 다양한 활성화 함수를 대체할 수 있음ELU: ReLU와 유사하지만 음수 입력에 대한 값을 부드럽게 하여 학습 안정성을 높임
Other Techniques
가중치 초기화
- 가중치 초기화에 따라 학습 성능과 모델 수렴 속도에 큰 영향을 미친다.
가중치 초기화 문제 상황 예시
- 모든 Weight를 0으로 초기화 하는 경우
→ 각 Weight에 대한 기울기가 동일해져 각 Weight가 동일한 방향으로 업데이트되어 결국 최적의 해에 도달할 수 없게 된다.
-
tanh activation을 사용하고 표준 정규분포에서 랜덤하게 뽑아서 상수를 곱해서 가중치를 초기화한다.
- 상수를 작은 값으로 주는 경우 → 학습을 진행할수록 activation값이 계속 작아지다가 0을 내뱉게됨
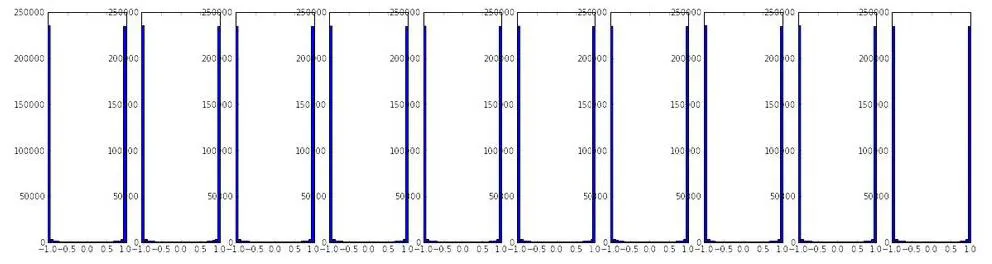
- 상수를 너무 큰 값으로 주는 경우 → 학습을 진행할 수록 activation이 1과 -1만 나오게됨
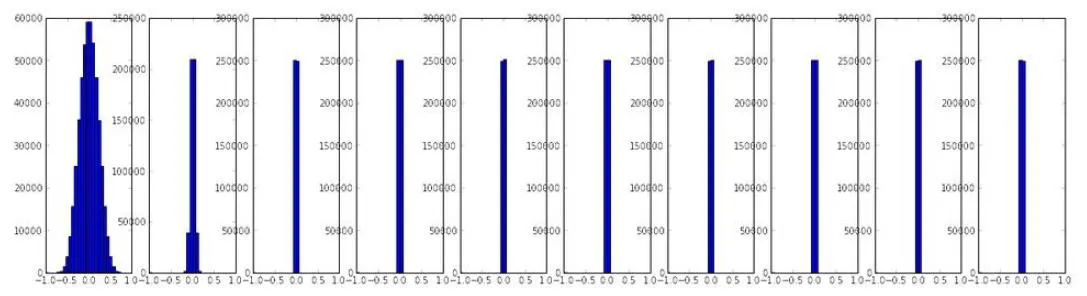
- 상수를 작은 값으로 주는 경우 → 학습을 진행할수록 activation값이 계속 작아지다가 0을 내뱉게됨
Xavier Initialization
- 가중치 초기화 방법의 한 종류이다.
- 각 층의 입력과 출력의 수에 따라 가중치를 설정한다.
- 이를 통해 가중치의 분산이 적절하게 유지되어, 신경망의 학습이 원활하게 진행된다.
- 활성화 함수의 비선형성을 고려하여 최적의 학습 속도를 보장한다.
→ 많은 activation을 거치더라도, 층을 통과하는 출력값들이 너무 크거나 작아지지 않도록 가중치를 초기화하여, 학습 초기 단계에서 출력값이 적절한 분포를 유지하도록 돕는다
Batch Normalization
문제 상황
- 이전 layer의 출력이 다음 layer의 입력으로 들어갈 때
-
activation function을 적용하지 않으면, layer를 깊게 쌓더라도 결국 하나의 layer를 쌓은 것과 동일한 효과를 낸다.
→ 이러한 이유로 비선형성을 추가하기 위해 non-linear한 activation function을 적용하게 된다.
-
- 하지만, ReLU와 같은 non-linear activation을 사용하더라도 출력 값들이 너무 큰 값이나 너무 작은 값에 몰리면 문제가 발생할 수 있다.
- 큰 값: 활성화 함수가 작동하여 값이 그대로 전달
- 작은 값: ReLU의 경우, 음수는 모두 0으로 출력되므로, 학습 중 dead neuron 문제가 생김
배치 정규화
- 신경망의 각 층에 들어가기 전에 정규화(Normalization)를 적용해 학습을 안정화하고 학습 속도를 높이는 방법이다.
- 입력에 대해 평균을 빼고 표준편차로 나누어 정규화한다. 이때 데이터가 특정 범위 내에 위치하도록 조정한다.
- 값에 다가 평균을 빼주고 표준편차로 나눠줘서 적절한 값에 놓이게 함
- 정규화 과정에서 사용되는 평균과 표준편차는 단순히 고정되지 않고, 학습 과정 중에 업데이트된다. 이를 통해 모델이 데이터의 분포 변화를 더 잘 반영할 수 있다.
→ 이를 통해 기울기 소실 문제를 줄이고, 더 높은 학습률을 사용할 수 있어 학습이 빨라진다. 또한, 과적합을 줄이는 데에도 도움이 된다
💡죽는 뉴런(Dead neuron)
- ReLU 활성화 함수에서 발생하는 문제로, 뉴런의 출력이 항상 0이 되어 학습 중 더 이상 업데이트되지 않는 현상을 말한다.
- ReLU는 음수 입력을 0으로 바꾸기 때문에, 학습 과정에서 뉴런이 "죽는" 문제가 생길 수 있다.
- 이를 방지하기 위해 Leaky ReLU 등 대안적인 활성화 함수가 사용된다
💡 배치 vs 미니배치 vs 확률적 경사 하강법 (SGD)
- 배치(Batch):
- 정의: 전체 데이터셋을 한 번에 처리해 가중치를 업데이트하는 방식
- 장점: 모든 데이터를 사용하므로 가중치 업데이트가 정확함
- 단점: 메모리 사용량이 크고, 학습 시간이 오래 걸림
- 미니배치(Mini-batch):
- 정의: 데이터셋을 작은 그룹으로 나눠 처리하고, 각 그룹 단위로 가중치를 업데이트
- 장점: 메모리 절감, 속도와 안정성의 균형을 제공
- 단점: 너무 작은 배치는 학습이 불안정할 수 있음
- 확률적 경사 하강법(SGD):
- 정의: 한 번에 하나의 데이터 포인트로 가중치를 업데이트
- 장점: 메모리 사용이 적고, 업데이트가 매우 빠름
- 단점: 업데이트가 불안정하고, 수렴 과정에서 진동이 발생할 수 있음