이 블로그글은 2019년 조재영(Kevin Jo), 김승수(SeungSu Kim)님의 딥러닝 홀로서기 세미나를 수강하고 작성한 글임을 밝힙니다.

💡 도움이 되셨다면 ♡와 팔로우 부탁드려요! 미리 감사합니다.

Optimizer

Gradient Descent

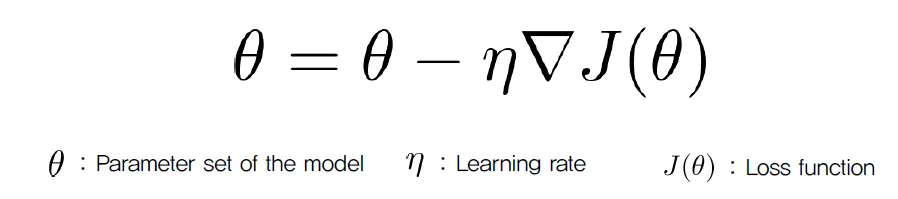
• 최적화 알고리즘으로, 최솟값(Minima)를 찾기 위해 gradient를 계산하여, gradient가 감소하는 방향으로 점점 이동하여 최솟값에 도달하게 하는 방법이다.

Batch Gradient Descent

• 한 iteration에 전체 데이터셋을 모두 사용하여 gradient를 계산한다.
• 특징
  • data에 의존하여 많은 메모리가 필요하다. (전체 데이터셋을 Ram에 올려야하기 때문)
  • 모든 데이터를 사용하여 gradient 계산하므로 느리고, 따라서 optimization이 느리다.

Stocastic Gradient Descent(SGD)

• 전체 데이터셋을 small chunk(mini-batch)로 나누어서 gradient를 계산한다.
• 특징
  • batch gradient descent와 비슷한 수렴 패턴을 보이지만, 보다 더 빠르다.
  • local minima에 빠지는 문제를 상대적으로 더 잘 해결한다. → *

💡 * 의 이유

• 전체 데이터셋을 사용하게 되면 gradient 진행 방향이 정해지면 그 경로로 일관되게 학습한다. (local minima에 머무를 가는성이 높음)
• 반면, SGD의 경우 방향을 모르므로 방향성을 유지하면서도 약간의 노이즈를 허용하여 local minima 벗어날 수 있는 방향으로 학습할 수 있다.

하지만, SGD는 지금부터 소개할 Adavanced Gradient Descent보다 느리고 여전히 한계가 있다.

Advanced Gradient Descent

SGD의 문제점

• 여전히 local minima에 갇힐 가능성이 높다.
• 두 가지 큰 방향성으로 문제점을 해결하고 이를 조합한 ADAM에 대해 이해해본다.
• 문제점

  • Local Minima에 갇힐 가능성

    → Momentum으로 해결

  • 모든 가중치가 동일한 크기로 변화 (동일한 학습률 적용)

    → Adaptive Learning Rate으로 해결

Momentum

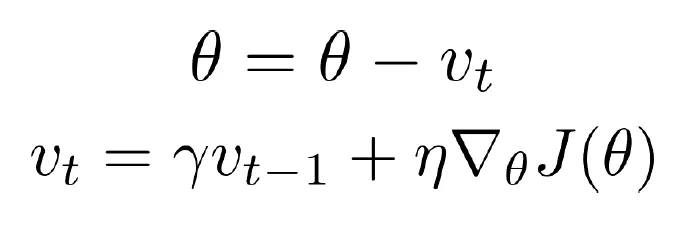
• 관성을 고려하자는 아이디어
• 매 step에서 loss의 편미분 값에 이전 step의 gradient 정보를 일부(γ : 0 ~ 1로 조절) 반영하여, local minima를 지나칠 수 있게 하자.
• 장점
  • 최적화가 일관된 방향으로 진행되며, 작은 지역 최솟값(local minima)에 갇히지 않도록 한다.
  • 경로가 진동하며 불안정하게 움직이는 현상인 Osiliating Problem을 해결하고 진동을 줄여주어 경로가 안정적이고 일관되게 수렴하도록 돕는다.
• 한계
  • Momentum이 지나치게 크면 global minima를 넘어가 overshooting(넘어가는 문제)이 발생할 수 있다.

Nesterov Accelerated Gradient (NAG)

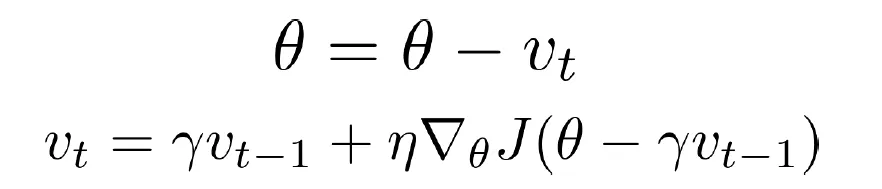
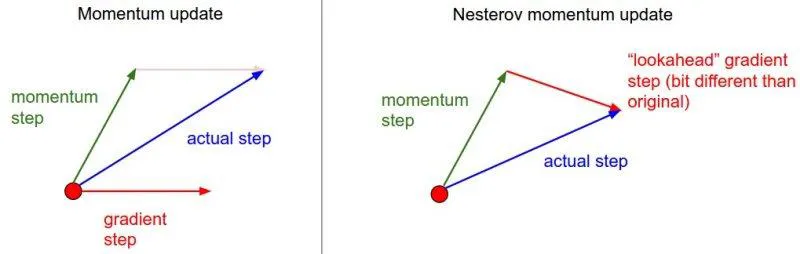
• 모멘텀을 고려하여 이동한 새로운 위치에서 gradient를 계산하자.
• 장점
  • 최적화 경로에서 벗어나거나, 지나치게 진동하는 현상을 줄여준다.

Adaptive Gradient (Adagrad)

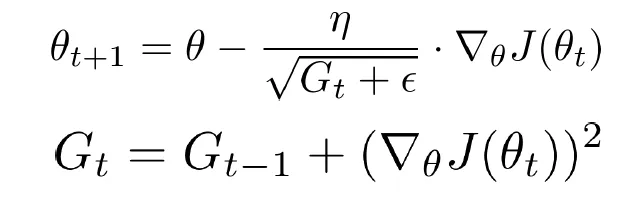
• Gₜ : 1 x k형태의 벡터 (k : 파라미터 수)
• Gₜ 는 파라미터의 gradient 제곱합을 누적하여 저장한다. (항상 양수)
• Gₜ 는 즉, 얼마나 가중치가 변화되었는가가 각각 저장된다.
• 학습률(learning rate)을 현재 스텝의 gradient와 함께 element-wise하게 나눠줌으로써, 각 파라미터의 학습률을 조정한다.
  • 많이 변화한 경우: 학습률이 작아짐
  • 적게 변화한 경우: 학습률이 커짐
• 참고) ϵ : 첫 스텝에서 Gₜ가 모두 0으로 초기화되어 있을 때 0으로 나누는 것을 방지하기 위해 더해줌
• 장점
  • 파라미터마다 학습률을 다르게 조정하여, 학습 과정에서 더 세밀한 조정이 가능해지고 최적화 과정이 안정적으로 이루어진다.
• 한계
  • Gₜ는 gradient 제곱합을 계속 누적하기 때문에 학습이 오래될수록 값이 커지고(발산), 이로 인해 스텝 크기(step size)가 점점 작아지고 결국엔 멈춰 버린다.

RMSProp

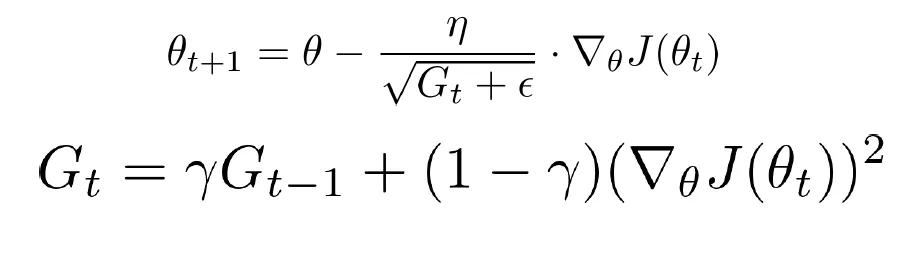
• *γ : Decaying constant (0~1)*
• γ를 사용하여 이전 스텝의 정보를 어느 정도 반영하면서, 최근 gradient의 변화에 가중치를 두어 누적된 값이 발산하지 않도록 합니다.
• 장점
  • 누적된 값이 발산하지 않도록 하여 학습이 멈추는 문제를 해결한다.

AdaDelta

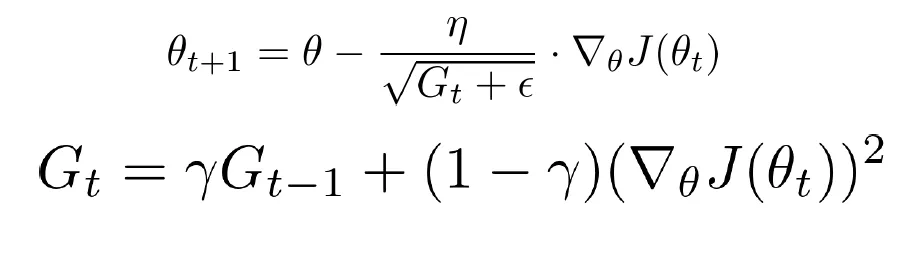
• Adagrad의 한계를 해결한 또 다른 형태
• 단위를 맞춰주자 는 아이디어
• θt의 단위를 u라 하자
• 핵심 : Δθ 의 단위를 u로 만들자, 더 정확한 계산이 가능할 것이다.

  • S의 단위 : u (파라미터 변화량 저장)

    • 분자에 루트가 씌워진 형태 : u의 제곱근

  • Gₜ의 단위 : u⁻² (gradient의 제곱의 누적합)

    • 분모에 루트가 씌어준 형태 : u⁻¹

  • 손실함수 편미분의 단위 : u⁻¹

    → 이들을 계산하면 최종 단위 : u

• 장점
  • 학습률을 직접 설정하지 않고도, 변화량에 기반해 자동으로 학습률을 조절하여 안정적 학습을 지원합니다.

Adaptive Moment Estimation (ADAM)

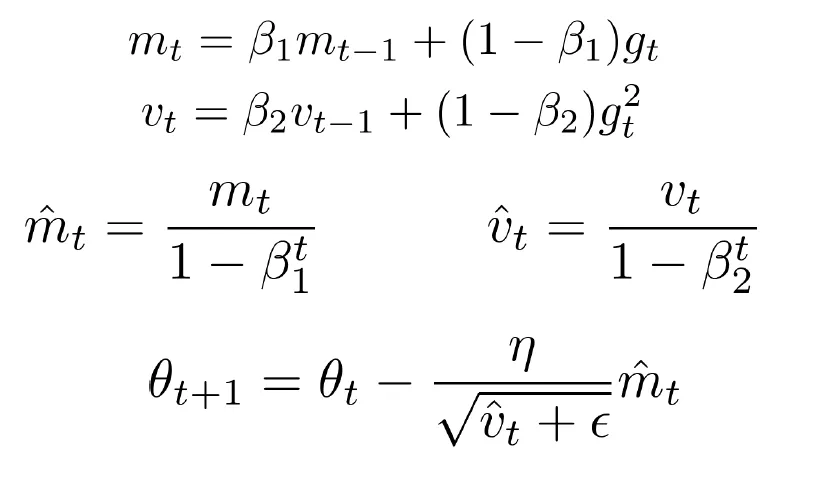
• 첫째 줄 : Momentum과 비슷한 효과를 주는 항
• 둘째 줄 : Adaptive Learning Rate를 적용하기 위해 사용하는 항
• 세번째 줄 : 첫 step에서 너무 큰 스텝을 밟지 않도록 조정하기 위한 식
  • 일반적으로 B₁를 B₂ 보다 작게 둔다. (예 : B₁ : 0.9, B₂ : 0.9999),
  • 첫 스텝에서 첫번째 항이 0이되고 남은 두번째항만 남아 너무step을 밟게 된다.
  • 이를 방지하기 위해 1-B₁ᵗ과 1-B₂ᵗ를 각각에 나눠줘 초기 단계의 스케일을 조정한다.
    • 스텝을 이어나감에 따라 각 식의 첫 번째 항(B₁mₜ₋₋₁, B₂mₜ ₋₋₁)의 역할이 더 커지게 됨으로 나중에는 크게 역할을 하지 않는다.
• 장점
  • 모멘텀과 RMSProp을 결합해, 초기 학습 속도를 높이면서도 수렴이 안정적입니다.

Pytorch에서 사용하는 방법

optimizer = optim.SGD(model.parameter(), lr = 0.01, momentum = 0.9)

• 위와 같이 optimizer를 설정할때, .SGD 대신 .Adagrad, .Adadelta, .RMSProp, .ADAM 로 바꾸어 사용할 수 있음
  • 단, optimizer마다 파라미터가 다르다.
• Momentum과 NAG의 경우 .SGD의 파라미터로 설정한다.
  • Momentum : momentum=0.9
  • NAG (Nesterov Accelerated Gradient) : nesterov=True